What is the limit 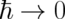 of quantum theory ?
of quantum theory ?
August 24, 2012
Abstract
An analysis is made of the relation between quantum theory and classical mechanics, in the context
of the limit 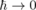 . Several ways in which this limit may be performed are considered. It is shown
that Schrödinger’s equation for a single particle moving in an external potential
. Several ways in which this limit may be performed are considered. It is shown
that Schrödinger’s equation for a single particle moving in an external potential 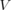 does not, except
for special cases, lead, in this limit, to Newtons equation of motion for the particle. This shows that
classical mechanics cannot be regarded as the limiting case of quantum mechanics for
does not, except
for special cases, lead, in this limit, to Newtons equation of motion for the particle. This shows that
classical mechanics cannot be regarded as the limiting case of quantum mechanics for 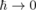 .
.