[1]   V. Allori and N. Zanghi. On the classical limit of quantum mechanics. Foundations of Physics, 39:20–32, 2009.

[2]   G. G. Cabrera and M. Kiwi. Large quantum-number states and the correspondence principle. Phys. Rev. A, 36:2995–2998, 1987.

[3]   J. Cohn. Quantum theory in the classical limit. Am. J. Phys., 40:463–467, 1972.

[4]   A. R. Usha Devi and H. S. Karthik. Uncertainty relations in the realm of classical dynamics. arXiv:1108.2682 [quant-ph].

[5]   J. J. Diamond. Classically forbidden behavior of the quantum harmonic oscillator for large quantum numbers. Am. J. Phys., 60(10):912–916, 1992.

[6]   P. A. M. Dirac. The principles of quantum mechanics. Oxford University Press, Oxford, 4. edition, 1958. p. 88.

[7]   A. Einstein, B. Podolsky, and N. Rosen. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev., 47(10):777–780, May 1935.

[8]   M. Gondran and A. Gondran. The two limits of the Schrödinger equation in the semi-classical approximation. arXiv:1107.0790, Proceedings of the 6th conference on ’Foundations of Physics and Probability’ (FFP6) Växjö 2011.

[9]   D. Home and S. Sengupta. Classical limit of quantum mechanics. Am. J. Phys., 51(3):265–267, 1983.

[10]   L. Kazandjian. The 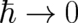limit of the Schrödinger equation. Am. J. Phys., 74:557, 2006.

[11]   U. Klein. Schrödinger’s equation with gauge coupling derived from a continuity equation. Foundations of physics, 39:964, 2009.

[12]   U. Klein. The statistical origins of quantum mechanics. Physics Research International, Article ID 808424, 2011.

[13]   D. H. Kobe. Comments on the classical limit of quantum mechanics. Am. J. Phys., 42:73–74, 1973.

[14]   L. Kocis. Ehrenfest theorem for the Hamilton-Jacobi equation. Acta Physica Polonica A, 102(6):709–716, 2002.

[15]   M. J. Lighthill. An introduction to Fourier analysis and generalized functions. Cambridge University Press, Cambridge, 1958.

[16]   Song Ling. On the 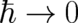limit of the Schrödinger equation. J. Chem. Phys., 96:7869–7870, 1992.

[17]   E. Madelung. Quantentheorie in hydrodynamischer Form. Z. Phys., 40:322–326, 1926.

[18]   H. Nikolic. Classical mechanics without determinism. Found. Phys. Lett., 19:553–566, 2006.

[19]   N. Rosen. The relation between classical and quantum mechanics. Am. J. Phys., 32:597–600, 1964.

[20]   E. G. P. Rowe. Classical limit of quantum mechanics (electron in a magnetic field). Am. J. Phys., 59:1111–1117, 1991.

[21]   R. Schiller. Quasi-classical theory of the nonspinning electron. Phys. Rev., 125(3):1100–1108, February 1962.

[22]   E. Schrödinger. The continuous transition from micro- to macro mechanics. Collected papers on wave mechanics, Chelsea Publishing, pages 41–44, 1982.

[23]   D. ter Haar. Selected problems in quantum mechanics. Infosearch Limited, London, 1964.

[24]   E. C. Titchmarsh. Introduction to the theory of Fourier integrals. Oxford, London, 1948. 2nd ed., Theorem 146 on p. 305.

[25]   R. F. Werner and M. P. H. Wolff. Classical mechanics as quantum mechanics with infinitesimal 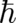. Physics Letters A, 202:155–159, 1995.

[26]   L. Zhou and L. M. Kuang. Coherent states: theory and some applications. Reviews of Modern Physics, 62:867–927, 1990.

[27]   I. Zlatev, W. Zhang, and D. H. Feng. Possibility that Schrödingers conjecture for the hydrogen-atom coherent states is not attainable. Physical Review, A 50(3):R1973–R1975, 1994.