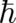 tends to zero”. A bright student, having read this
statement might ask his teacher the following question: ”In quantum mechanics a single particle in an external
potential is described by Schrödinger’s equation
tends to zero”. A bright student, having read this
statement might ask his teacher the following question: ”In quantum mechanics a single particle in an external
potential is described by Schrödinger’s equation
In Dirac’s famous book [6] on quantum theory one finds the statement: ”...classical mechanics may be regarded
as the limiting case of quantum mechanics when 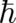 tends to zero”. A bright student, having read this
statement might ask his teacher the following question: ”In quantum mechanics a single particle in an external
potential is described by Schrödinger’s equation
tends to zero”. A bright student, having read this
statement might ask his teacher the following question: ”In quantum mechanics a single particle in an external
potential is described by Schrödinger’s equation
![[ 3 ( ) ]
ℏ ∂ ℏ2 ∑ ∂ 2
------- ------ -------
- + V (x, t ) ψ (x, t ) = 0.
i ∂ t 2m ∂ xk
k=1](climit7x.png) | (1) |
If Dirac is right then Newton’s equation,
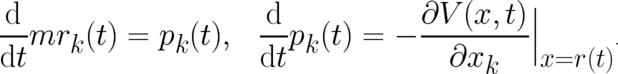 | (2) |
should follow from Schrödinger’s equation in the limit  . Can you tell us, how this calculation is
actually performed ? ” Nobody has ever performed a general exact calculation showing that (1) implies (2) in
the limit
. Can you tell us, how this calculation is
actually performed ? ” Nobody has ever performed a general exact calculation showing that (1) implies (2) in
the limit 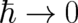 . An experienced teacher will nevertheless find an answer to this question. We will not
discuss the variety of his possible responses but think that these will probably not include one of the following
two statements: (i) Dirac is wrong, (ii) the answer is not known. A typical response is the statement that this
limit cannot be understood in such a simple way. A closer look in Dirac’s book shows, however, that, at least as
Dirac’s original intentions are concerned, this statement should in fact be interpreted in this simple
way.
. An experienced teacher will nevertheless find an answer to this question. We will not
discuss the variety of his possible responses but think that these will probably not include one of the following
two statements: (i) Dirac is wrong, (ii) the answer is not known. A typical response is the statement that this
limit cannot be understood in such a simple way. A closer look in Dirac’s book shows, however, that, at least as
Dirac’s original intentions are concerned, this statement should in fact be interpreted in this simple
way.
The attitude of the scientific community with regard to this point - which is extremely important for the
interpretation of quantum theory (QT) as well as for more general questions such as the problem of reductionism
- is somewhat schizophrenic. On the one hand, Dirac’s dictum - which has been approved by other great
physicists - is considered to be true. On the other hand it cannot be verified. Since the beginnings of QT a never
ending series of works deal with this question, but the deterministic limit of QT, in the sense of
the above general statement, has never been attained. Frequently, isolated ’classical properties’
which indicate asymptotic ’nearness’ of deterministic physics, or structural similarities (such as
those between Poisson brackets and commutators) are considered as a substitute for the limit.
The point is that in most of these papers (see e.g. [20],[25],[1] to mention only a few) the question
”what is the limit 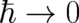 of quantum theory ?” is not studied. It is taken for granted that
the final answer to this question has already been given (by Dirac and others) and the remaining
problem is just how to confirm, or illustrate it by concrete calculations. But none of these attempts is
satisfying.
of quantum theory ?” is not studied. It is taken for granted that
the final answer to this question has already been given (by Dirac and others) and the remaining
problem is just how to confirm, or illustrate it by concrete calculations. But none of these attempts is
satisfying.
In the present paper the question formulated in the title will be studied without knowing the answer. A detailed
step-by-step style of exposition has been chosen in order to understand this singular limit. In fact, the paper has
been written with the idea in mind to provide an in-depth answer to a student’s question concerning the
mathematical details of the transition from (1) to (2). The questions how to perform a limit and how to
characterize the relations between different (related) physical theories are closely connected to the basic question
how to characterize physical theories themselves. We take a pragmatic position with respect to this question
and characterize a physical theory simply by the set of its predictions. It turns out that this leads
automatically to a reasonable definition of limit relations between different physical theories. We start by
discussing, in section 2, two well-understood concrete limiting relations between two pairs of classical
physical theories. These classical limiting relations, referred to as ’standard limit’ and ’deterministic
limit’, define possible meanings of the term ”the limit 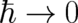 ” in QT. In section 3 we use
the variables introduced by Madelung to obtain the ’standard limit’ of QT, previously found by
Rosen [19], Schiller [21] and others. In section 4 we derive the deterministic limit of the ’standard limit’
of QT. We find that Ehrenfest’s relations, which have not been taken into account in previous
treatments [19, 3, 13, 18, 8], provide the missing link between the ’standard limit’ (field) theory and the
trajectory equations of Newtonian mechanics (NM). In section 5 we investigate the ’deterministic
limit’ of QT and conclude that this limit does not exist. In section 6 we try to reconstruct the
states of NM from QT by combining the ’deterministic limit’ and the ’standard limit’. In this way
we are indeed able to identify a class of (three) potentials and states which allow for a transition
from QT to NM in the limit
” in QT. In section 3 we use
the variables introduced by Madelung to obtain the ’standard limit’ of QT, previously found by
Rosen [19], Schiller [21] and others. In section 4 we derive the deterministic limit of the ’standard limit’
of QT. We find that Ehrenfest’s relations, which have not been taken into account in previous
treatments [19, 3, 13, 18, 8], provide the missing link between the ’standard limit’ (field) theory and the
trajectory equations of Newtonian mechanics (NM). In section 5 we investigate the ’deterministic
limit’ of QT and conclude that this limit does not exist. In section 6 we try to reconstruct the
states of NM from QT by combining the ’deterministic limit’ and the ’standard limit’. In this way
we are indeed able to identify a class of (three) potentials and states which allow for a transition
from QT to NM in the limit  ; these include among others the coherent states of the
harmonic oscillator [22]. In section 7 we try to extend this process to arbitrary potentials. The
obtained results are discussed and interpreted in section 8 and the final conclusion is drawn in
section 9.
; these include among others the coherent states of the
harmonic oscillator [22]. In section 7 we try to extend this process to arbitrary potentials. The
obtained results are discussed and interpreted in section 8 and the final conclusion is drawn in
section 9.