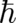 )
appears in QT; this indicates the possibility to obtain NM from QT by means of a ’standard’ limiting process.
This shows that the limiting process which leads from QT to NM is either nonexistent or more complex than any
one of the above examples.
)
appears in QT; this indicates the possibility to obtain NM from QT by means of a ’standard’ limiting process.
This shows that the limiting process which leads from QT to NM is either nonexistent or more complex than any
one of the above examples.
Let us now compare QT and NM [Eqs. (1) and (2)] in the light of the above examples. Both theories differ
obviously with respect to their mathematical structure; this indicates the possibility to obtain NM from QT by
means of a ’deterministic’ limiting process. However, in addition, a new fundamental constant (the number 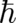 )
appears in QT; this indicates the possibility to obtain NM from QT by means of a ’standard’ limiting process.
This shows that the limiting process which leads from QT to NM is either nonexistent or more complex than any
one of the above examples.
)
appears in QT; this indicates the possibility to obtain NM from QT by means of a ’standard’ limiting process.
This shows that the limiting process which leads from QT to NM is either nonexistent or more complex than any
one of the above examples.
Let us try, as a first step, to perform the ’standard limit’ of QT - as defined by the first example in section 2.
Performing the limit 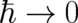 in Eq. (1) produces a nonsensical result. This indicates that the real
and imaginary parts of
in Eq. (1) produces a nonsensical result. This indicates that the real
and imaginary parts of 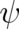 are not appropriate variables with regard to this limiting process;
probably because they become singular in the limit
are not appropriate variables with regard to this limiting process;
probably because they become singular in the limit  . Thus, a different set of dynamical
variables should be chosen, which behaves regular in this limit. There is convincing evidence, from
various physical contexts, that appropriate variables, denoted by
. Thus, a different set of dynamical
variables should be chosen, which behaves regular in this limit. There is convincing evidence, from
various physical contexts, that appropriate variables, denoted by 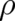 and
and 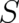 , are defined by the
transformation
, are defined by the
transformation
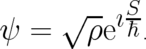 | (7) |
This transformation has been introduced by Madelung [17]. Note that using these variables in
a meaningful limiting process requires that the modulus of 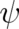 remains regular while its phase
diverges like
remains regular while its phase
diverges like 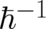 for small
for small 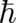 . This singular behavior, which has been noted very early [?], is
the behavior of the majority of ’well-behaved’ quantum states. Other, more singular, states may,
however, behave in a different manner and will then require a different factorization in terms of
. This singular behavior, which has been noted very early [?], is
the behavior of the majority of ’well-behaved’ quantum states. Other, more singular, states may,
however, behave in a different manner and will then require a different factorization in terms of 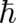 .
This may also lead to different equations in the limit
.
This may also lead to different equations in the limit 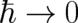 ; an example will be given in
section 6.
; an example will be given in
section 6.
In terms of the new variables Schrödinger’s equation takes the form of two coupled nonlinear differential
equations. The first is a continuity equation which does not contain 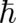 ,
,
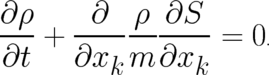 | (8) |
The second equation contains 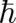 as a proportionality factor in front of a single term,
as a proportionality factor in front of a single term,
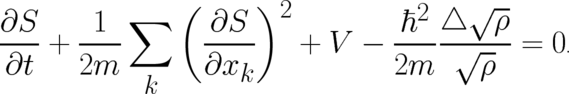 | (9) |
Eq. (9) is referred to as quantum Hamilton-Jacobi equation (QHJ). The 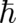 -dependent ’quantum term’ in (9)
describes the influence of
-dependent ’quantum term’ in (9)
describes the influence of 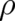 on
on 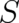 (It is frequently denoted as ”quantum potential”, which is
an extremely misleading nomenclature because a potential is, as a rule, an externally controlled
quantity). Its physical meaning, as interpreted by the present author, has been discussed in more detail
elsewhere [11].
(It is frequently denoted as ”quantum potential”, which is
an extremely misleading nomenclature because a potential is, as a rule, an externally controlled
quantity). Its physical meaning, as interpreted by the present author, has been discussed in more detail
elsewhere [11].
In the limit 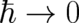 the quantum term disappears. Thus the ’standard limit’ of QT is given by two partial
differential equations, the continuity equation (8), which depends on
the quantum term disappears. Thus the ’standard limit’ of QT is given by two partial
differential equations, the continuity equation (8), which depends on 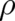 and
and 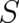 , and the Hamilton-Jacobi
(HJ) equation,
, and the Hamilton-Jacobi
(HJ) equation,
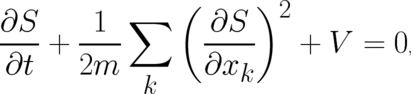 | (10) |
which depends only on 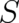 . The two equations (8) and (10) which will be referred to as probabilistic
Hamilton-Jacobi theory (PHJ) constitute the classical limit of Schrödinger’s equation or ’single-particle’ QT,
respectively. Clearly, this limit does not agree with the trajectory equations (2) of NM.
. The two equations (8) and (10) which will be referred to as probabilistic
Hamilton-Jacobi theory (PHJ) constitute the classical limit of Schrödinger’s equation or ’single-particle’ QT,
respectively. Clearly, this limit does not agree with the trajectory equations (2) of NM.
Much confusion has been created by the fact, that the Hamilton-Jacobi formulation of classical mechanics allows
the determination of particle trajectories with the help of the HJ equation. From the fact that this equation can
be obtained from QT in the limit 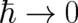 it is often concluded, neglecting the continuity equation, that
classical mechanics is the
it is often concluded, neglecting the continuity equation, that
classical mechanics is the 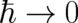 limit of QT. However, the limit
limit of QT. However, the limit 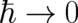 of QT does not provide us
with the theory of canonical transformations, which is required to actually calculate particle trajectories. Note
also that for exactly those quantum-mechanical states which are most similar to classical states
(e.g. coherent states, see section 6) the classical limit of QHJ differs from HJ. There is in fact a
connection between the PHJ and NM but this requires a second limiting process, as will be explained in
section 4.
of QT does not provide us
with the theory of canonical transformations, which is required to actually calculate particle trajectories. Note
also that for exactly those quantum-mechanical states which are most similar to classical states
(e.g. coherent states, see section 6) the classical limit of QHJ differs from HJ. There is in fact a
connection between the PHJ and NM but this requires a second limiting process, as will be explained in
section 4.
Both the PHJ and its (standard) covering theory QT are probabilistic theories, which provide statistical
predictions (probabilities and expectation values) if initial values for 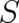 and
and 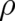 are specified. Although we
have now partial differential equations, the relation between QT and PHJ resembles in essential aspects the
relation between relativistic mechanics and NM.
are specified. Although we
have now partial differential equations, the relation between QT and PHJ resembles in essential aspects the
relation between relativistic mechanics and NM.