6 The ’combined limit’ of quantum theory
Let us summarize what has been achieved so far. In section 3 the limit 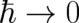 has been performed for
arbitrary states (including wave packets with fixed width
has been performed for
arbitrary states (including wave packets with fixed width 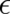 ). The result of this first ’standard limiting process’
was a classical statistical theory referred to as PHJ. In section 4 the limit
). The result of this first ’standard limiting process’
was a classical statistical theory referred to as PHJ. In section 4 the limit 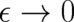 of PHJ has been
performed. The result of this second ’deterministic limit’ was NM. Therefore NM is a subset of the classical limit
PHJ of QT but NM is not the classical limit of QT, since we cannot neglect almost all of the (statistical)
states of PHJ. Thus, the two limiting processes performed in this order have not led us from QT to
NM in the sense that NM can be said to be the classical limit
of PHJ has been
performed. The result of this second ’deterministic limit’ was NM. Therefore NM is a subset of the classical limit
PHJ of QT but NM is not the classical limit of QT, since we cannot neglect almost all of the (statistical)
states of PHJ. Thus, the two limiting processes performed in this order have not led us from QT to
NM in the sense that NM can be said to be the classical limit 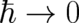 of QT. In section 5
it has been shown that inverting the order of the two limiting processes (first
of QT. In section 5
it has been shown that inverting the order of the two limiting processes (first 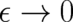 then
then
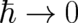 ) does not solve the problem either since the limit
) does not solve the problem either since the limit 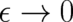 (with
(with 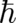 fixed)
does not exist. The two limiting processes clearly do not commute. Thus, it is impossible to obtain
NM as the classical limit of QT, no matter which order of the two (separate) limiting processes is
chosen.
fixed)
does not exist. The two limiting processes clearly do not commute. Thus, it is impossible to obtain
NM as the classical limit of QT, no matter which order of the two (separate) limiting processes is
chosen.
Fortunately, we have still the option to combine both limits; i.e. we could assume that the width of the wave
packets is a monotone function of 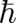 . This means that the localization of wave packets (the ’deterministic
limit’) and the change of the basic equations of QT (the ’standard limit’) takes place simultaneously in the limit
. This means that the localization of wave packets (the ’deterministic
limit’) and the change of the basic equations of QT (the ’standard limit’) takes place simultaneously in the limit
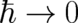 . Such states seem artificial from the point of view of experimental verification since the numerical
value of
. Such states seem artificial from the point of view of experimental verification since the numerical
value of 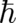 is not under our control. Nevertheless, a construction of NM from QT along these lines
would certainly provide a kind of justification for Dirac’s claim that QT reduces to NM in the limit
is not under our control. Nevertheless, a construction of NM from QT along these lines
would certainly provide a kind of justification for Dirac’s claim that QT reduces to NM in the limit
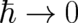 . Note also, that the subject of our study is essentially of a formal nature. We are
asking whether or not all predictions of NM can be obtained by means of some limiting process
. Note also, that the subject of our study is essentially of a formal nature. We are
asking whether or not all predictions of NM can be obtained by means of some limiting process
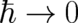 , from the basic equations of QT. There are no in-principle constraints how to perform his
limit.
, from the basic equations of QT. There are no in-principle constraints how to perform his
limit.
A brief look at the above examples for 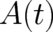 shows that a linear relation between
shows that a linear relation between 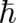 and
and 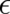 seems most
promising. Thus, we set ,
seems most
promising. Thus, we set ,
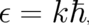 | (25) |
were 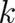 is an arbitrary constant. In order to use a notation similar to section 4 [see (11)],
is an arbitrary constant. In order to use a notation similar to section 4 [see (11)], 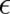 will be used
instead of
will be used
instead of 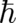 as small parameter; it may be identified with
as small parameter; it may be identified with 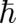 in most of the following relations. Let
us perform the identification (25) for the two examples considered in section 5, with potentials
in most of the following relations. Let
us perform the identification (25) for the two examples considered in section 5, with potentials
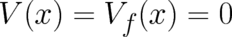 and
and 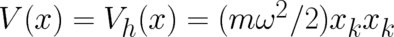 ,
respectively. Using the same initial conditions as in section 5, the solutions for
,
respectively. Using the same initial conditions as in section 5, the solutions for 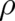 and
and 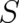 of (8), (9) take
essentially the same form in both cases, namely
of (8), (9) take
essentially the same form in both cases, namely
The solutions 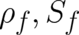 and
and 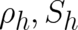 for particle ensembles in force-free regions and linear-force
fields may be obtained from Eqs. (26), (27) by using different widths
for particle ensembles in force-free regions and linear-force
fields may be obtained from Eqs. (26), (27) by using different widths 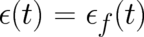 and
and
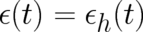 , as given by
, as given by
![( )
2 [ ]
t 2 1 2
ϵf (t ) = ϵ 1 + --------- , ϵh (t ) = ϵ cos ωt + ------------- sin ωt ,
k2m2 k2m2 ω2](climit171x.png) | (28) |
and different trajectory components 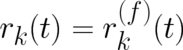 and
and 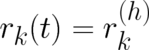 (as well as
momentum components
(as well as
momentum components 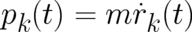 ), as given by
), as given by
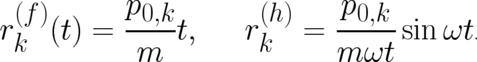 | (29) |
As Eq. (28) shows, both widths are time-dependent; for the free-particle ensemble the width increases
quadratically, for the bounded motion of the harmonic oscillator it varies periodically. However, both widths
vanish in the limit 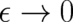 for arbitrary (finite) times
for arbitrary (finite) times 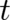 . This means that the deterministic probability
density we were looking for is, in fact, created in this limit. The solutions for
. This means that the deterministic probability
density we were looking for is, in fact, created in this limit. The solutions for 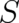 are well-behaved at
are well-behaved at
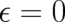 . The limiting process in the continuity equation (8) can be performed in a similar way as in
section 4 (an additional term due to the time-dependence of
. The limiting process in the continuity equation (8) can be performed in a similar way as in
section 4 (an additional term due to the time-dependence of 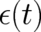 is regular at
is regular at 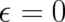 ). The remaining
steps, the derivation of Newton’s equations and their field-theoretic derivation from the QHJ can be
performed in the same way as in section 4. Note also that the QHJ is regular at
). The remaining
steps, the derivation of Newton’s equations and their field-theoretic derivation from the QHJ can be
performed in the same way as in section 4. Note also that the QHJ is regular at 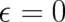 and
differs in this limit from the HJ equation [cf. the discussion following Eq. (7)]. In view of a recent
discussion [16], [10] it should be noted that this field-theoretic limit is not equivalent to its projection on the
trajectory.
and
differs in this limit from the HJ equation [cf. the discussion following Eq. (7)]. In view of a recent
discussion [16], [10] it should be noted that this field-theoretic limit is not equivalent to its projection on the
trajectory.
The above solutions, with 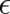 and
and 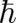 considered as independent parameters (as in section 5), have been
reported many times in the literature. It has also been pointed out that the special value
considered as independent parameters (as in section 5), have been
reported many times in the literature. It has also been pointed out that the special value 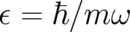 ,
in the harmonic oscillator example, produces the coherent states found by Schrödinger [22]. On the
other hand, the relevance of the weaker statement
,
in the harmonic oscillator example, produces the coherent states found by Schrödinger [22]. On the
other hand, the relevance of the weaker statement 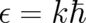 for the classical limit problem has
apparently not been recognized. It is not necessary to restrict oneself to the coherent states of the
harmonic oscillator (the special case
for the classical limit problem has
apparently not been recognized. It is not necessary to restrict oneself to the coherent states of the
harmonic oscillator (the special case 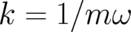 ) in order to obtain deterministic motion; the
latter may be obtained for a much larger class of force-free states, harmonic oscillator states, and
constant-force states (this last example has not been discussed explicitly) as shown above. Summarizing this
section, we found three potentials
) in order to obtain deterministic motion; the
latter may be obtained for a much larger class of force-free states, harmonic oscillator states, and
constant-force states (this last example has not been discussed explicitly) as shown above. Summarizing this
section, we found three potentials 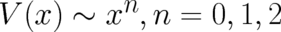 which allow for a
derivation of NM from QT in the limit
which allow for a
derivation of NM from QT in the limit 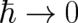 . For these potentials equations of motion for
. For these potentials equations of motion for
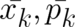 exist, as mentioned already. Home and Sengupta [9] have shown that for these potentials the
form of the quantum-mechanical solution may be obtained with the help of the classical Liouville
theorem.
exist, as mentioned already. Home and Sengupta [9] have shown that for these potentials the
form of the quantum-mechanical solution may be obtained with the help of the classical Liouville
theorem.
 has been performed for
arbitrary states (including wave packets with fixed width
has been performed for
arbitrary states (including wave packets with fixed width 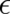 ). The result of this first ’standard limiting process’
was a classical statistical theory referred to as PHJ. In section 4 the limit
). The result of this first ’standard limiting process’
was a classical statistical theory referred to as PHJ. In section 4 the limit 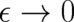 of PHJ has been
performed. The result of this second ’deterministic limit’ was NM. Therefore NM is a subset of the classical limit
PHJ of QT but NM is not the classical limit of QT, since we cannot neglect almost all of the (statistical)
states of PHJ. Thus, the two limiting processes performed in this order have not led us from QT to
NM in the sense that NM can be said to be the classical limit
of PHJ has been
performed. The result of this second ’deterministic limit’ was NM. Therefore NM is a subset of the classical limit
PHJ of QT but NM is not the classical limit of QT, since we cannot neglect almost all of the (statistical)
states of PHJ. Thus, the two limiting processes performed in this order have not led us from QT to
NM in the sense that NM can be said to be the classical limit  of QT. In section 5
it has been shown that inverting the order of the two limiting processes (first
of QT. In section 5
it has been shown that inverting the order of the two limiting processes (first  then
then
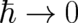 ) does not solve the problem either since the limit
) does not solve the problem either since the limit  (with
(with 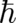 fixed)
does not exist. The two limiting processes clearly do not commute. Thus, it is impossible to obtain
NM as the classical limit of QT, no matter which order of the two (separate) limiting processes is
chosen.
fixed)
does not exist. The two limiting processes clearly do not commute. Thus, it is impossible to obtain
NM as the classical limit of QT, no matter which order of the two (separate) limiting processes is
chosen.
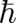 . This means that the localization of wave packets (the ’deterministic
limit’) and the change of the basic equations of QT (the ’standard limit’) takes place
. This means that the localization of wave packets (the ’deterministic
limit’) and the change of the basic equations of QT (the ’standard limit’) takes place 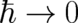 . Such states seem artificial from the point of view of experimental verification since the numerical
value of
. Such states seem artificial from the point of view of experimental verification since the numerical
value of 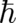 is not under our control. Nevertheless, a construction of NM from QT along these lines
would certainly provide a kind of justification for Dirac’s claim that QT reduces to NM in the limit
is not under our control. Nevertheless, a construction of NM from QT along these lines
would certainly provide a kind of justification for Dirac’s claim that QT reduces to NM in the limit
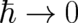 . Note also, that the subject of our study is essentially of a formal nature. We are
asking whether or not all predictions of NM can be obtained by means of some limiting process
. Note also, that the subject of our study is essentially of a formal nature. We are
asking whether or not all predictions of NM can be obtained by means of some limiting process
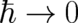 , from the basic equations of QT. There are no in-principle constraints how to perform his
limit.
, from the basic equations of QT. There are no in-principle constraints how to perform his
limit.
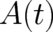 shows that a
shows that a 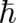 and
and 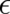 seems most
promising. Thus, we set ,
seems most
promising. Thus, we set ,
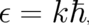
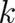 is an arbitrary constant. In order to use a notation similar to section
is an arbitrary constant. In order to use a notation similar to section 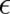 will be used
instead of
will be used
instead of 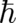 as small parameter; it may be identified with
as small parameter; it may be identified with 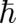 in most of the following relations. Let
us perform the identification (
in most of the following relations. Let
us perform the identification (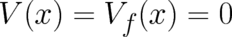 and
and 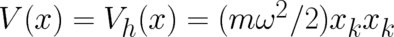 ,
respectively. Using the same initial conditions as in section
,
respectively. Using the same initial conditions as in section 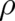 and
and 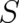 of (
of (![( )
( ) 3- { 3 }
1 2 1 ∑ 2
ρ (x, t) = --------- exp - ------ [x - r (t) ] , (26)
π ϵ(t ) ( ϵ (t) k k )
k=1
3 3
m ϵ˙(t ) ∑ 1 ∑ ϵ r (t )
S (x, t) = ---------- [x - r (t ) ]2 - --p (t )r (t ) + p (t)x - ---- tan - 1 ---i---(27.)
i i k k k k
4 ϵ (t ) 2 2k kpi (t)
i=1 i=1](climit166x.png)
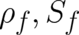 and
and 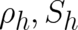 for particle ensembles in force-free regions and linear-force
fields may be obtained from Eqs. (26), (27) by using different widths
for particle ensembles in force-free regions and linear-force
fields may be obtained from Eqs. (26), (27) by using different widths 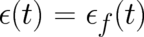 and
and
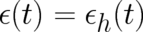 , as given by
, as given by
![( )
2 [ ]
t 2 1 2
ϵf (t ) = ϵ 1 + --------- , ϵh (t ) = ϵ cos ωt + ------------- sin ωt ,
k2m2 k2m2 ω2](climit171x.png)
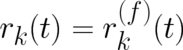 and
and 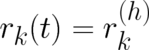 (as well as
momentum components
(as well as
momentum components 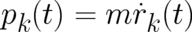 ), as given by
), as given by
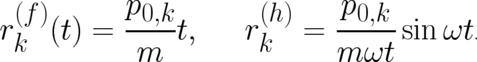
 for arbitrary (finite) times
for arbitrary (finite) times  . This means that the deterministic probability
density we were looking for is, in fact, created in this limit. The solutions for
. This means that the deterministic probability
density we were looking for is, in fact, created in this limit. The solutions for  are well-behaved at
are well-behaved at
 . The limiting process in the continuity equation (
. The limiting process in the continuity equation (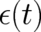 is regular at
is regular at 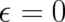 ). The remaining
steps, the derivation of Newton’s equations and their field-theoretic derivation from the QHJ can be
performed in the same way as in section
). The remaining
steps, the derivation of Newton’s equations and their field-theoretic derivation from the QHJ can be
performed in the same way as in section  and
and
 and
and 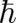 considered as
considered as 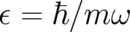 ,
in the harmonic oscillator example, produces the coherent states found by Schrödinger
,
in the harmonic oscillator example, produces the coherent states found by Schrödinger 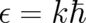 for the classical limit problem has
apparently not been recognized. It is not necessary to restrict oneself to the coherent states of the
harmonic oscillator (the special case
for the classical limit problem has
apparently not been recognized. It is not necessary to restrict oneself to the coherent states of the
harmonic oscillator (the special case 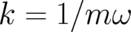 ) in order to obtain deterministic motion; the
latter may be obtained for a much larger class of force-free states, harmonic oscillator states, and
constant-force states (this last example has not been discussed explicitly) as shown above. Summarizing this
section, we found three potentials
) in order to obtain deterministic motion; the
latter may be obtained for a much larger class of force-free states, harmonic oscillator states, and
constant-force states (this last example has not been discussed explicitly) as shown above. Summarizing this
section, we found three potentials 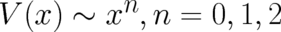 which allow for a
derivation of NM from QT in the limit
which allow for a
derivation of NM from QT in the limit 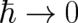 . For these potentials equations of motion for
. For these potentials equations of motion for
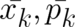 exist, as mentioned already. Home and Sengupta
exist, as mentioned already. Home and Sengupta