 . We shall refer to such potentials for brevity as ’deterministic
potentials’. A (complete) reconstruction of NM from QT requires that all (or almost all) potentials are
deterministic. In this section we ask if this can be true.
. We shall refer to such potentials for brevity as ’deterministic
potentials’. A (complete) reconstruction of NM from QT requires that all (or almost all) potentials are
deterministic. In this section we ask if this can be true.
We know now that three potentials exist which, for properly chosen initial wave-packets, lead to deterministic
equations of motion in the limit  . We shall refer to such potentials for brevity as ’deterministic
potentials’. A (complete) reconstruction of NM from QT requires that all (or almost all) potentials are
deterministic. In this section we ask if this can be true.
. We shall refer to such potentials for brevity as ’deterministic
potentials’. A (complete) reconstruction of NM from QT requires that all (or almost all) potentials are
deterministic. In this section we ask if this can be true.
As a first point we note that the probability density 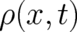 of all deterministic wave packets takes,
by definition, a very specific functional form, namely one that reduces, like Eq. (26), in the limit
of all deterministic wave packets takes,
by definition, a very specific functional form, namely one that reduces, like Eq. (26), in the limit
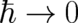 to a delta function. This fixes essentially one of our two dynamic variables; we have
two differential equations for a single unknown variable
to a delta function. This fixes essentially one of our two dynamic variables; we have
two differential equations for a single unknown variable 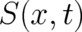 . It seems unlikely that this
overdetermined system of equations admits solutions for
. It seems unlikely that this
overdetermined system of equations admits solutions for 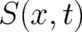 for arbitrary potentials
for arbitrary potentials
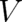 .
.
The second point to note is, that the existence of a deterministic limit does not only fix the functional form of
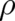 but also its argument. Let us assume, that a deterministic solution for
but also its argument. Let us assume, that a deterministic solution for 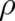 and
and 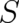 , with
, with 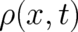 taking the form (26) with unspecified
taking the form (26) with unspecified 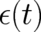 , exists. The probability density
, exists. The probability density 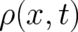 depends
necessarily on
depends
necessarily on 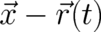 , where the position vector
, where the position vector 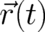 is a solution of Newton’s equation for the
same potential
is a solution of Newton’s equation for the
same potential 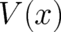 that occurs in the Schrödinger equation. The crucial point is that this dependence is
not created by the limiting process
that occurs in the Schrödinger equation. The crucial point is that this dependence is
not created by the limiting process 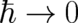 but is already present for finite
but is already present for finite 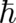 , in the exact
quantum-mechanical solution. For given initial conditions it has been created, so to say, by the
quantum-theoretical formalism. This implies that
, in the exact
quantum-mechanical solution. For given initial conditions it has been created, so to say, by the
quantum-theoretical formalism. This implies that 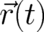 describes for finite
describes for finite 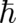 not the time-dependence of a
particle trajectory but of a position expectation value. Since
not the time-dependence of a
particle trajectory but of a position expectation value. Since 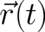 is (again for finite
is (again for finite 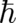 ) the
solution of Newton’s equations, such equations for expectation values must already be present in the
quantum-theoretical formalism. Of course, in the deterministic limit
) the
solution of Newton’s equations, such equations for expectation values must already be present in the
quantum-theoretical formalism. Of course, in the deterministic limit 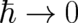 the difference between
particle trajectories and expectation values vanishes, but the important point is that Newton’s
equations must hold already for finite
the difference between
particle trajectories and expectation values vanishes, but the important point is that Newton’s
equations must hold already for finite 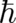 . We conclude that the existence of the equations of motion
of NM for position expectation values is a necessary condition for the existence of deterministic
potentials.
. We conclude that the existence of the equations of motion
of NM for position expectation values is a necessary condition for the existence of deterministic
potentials.
This line of reasoning leads to a mathematical condition for deterministic potentials. Let us assume that we have
a deterministic potential 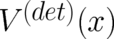 in our quantum-theoretical (
in our quantum-theoretical (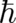 finite) problem. We calculate the
expectation value
finite) problem. We calculate the
expectation value 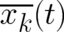 as defined by (17) using the deterministic probability density (26). We obtain
as defined by (17) using the deterministic probability density (26). We obtain
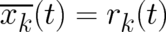 , i.e. the expectation value follows the time-dependence of the trajectory
[the peak of
, i.e. the expectation value follows the time-dependence of the trajectory
[the peak of 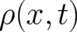 ]. The latter must fulfill Newton’s equation with the force derived from
]. The latter must fulfill Newton’s equation with the force derived from
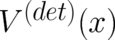 , otherwise the deterministic limit could not exist. Using these facts in Ehrenfest’s
theorems (15) and (16) we obtain immediately the following integral equation for deterministic
potentials
, otherwise the deterministic limit could not exist. Using these facts in Ehrenfest’s
theorems (15) and (16) we obtain immediately the following integral equation for deterministic
potentials
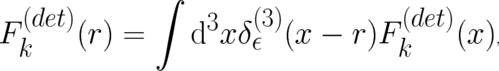 | (30) |
where 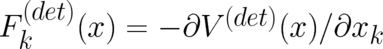 . The quantity
. The quantity 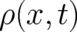 has been
renamed
has been
renamed 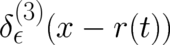 in order to show the convolution-type structure of the equation. Note
that (30) is only for
in order to show the convolution-type structure of the equation. Note
that (30) is only for 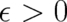 a constraint for
a constraint for 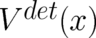 . It is easy to see that a particular solution is
given by
. It is easy to see that a particular solution is
given by 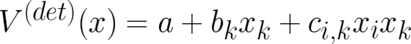 , where the coefficients may depend on
time. This is essentially a linear combination of the three deterministic potentials
, where the coefficients may depend on
time. This is essentially a linear combination of the three deterministic potentials 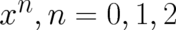 found already in the last section. According to a theorem by Titchmarsh [24] (a simple proof may be
obtained with the help of the theory of generalized functions [15], see section 10) other solutions
of (30) do not exist. This theorem shows that the ’combined limit’ cannot be performed for all
potentials. Although the present treatment does not cover all conceivable physical situations, the results
obtained so far imply already definitively that the limit
found already in the last section. According to a theorem by Titchmarsh [24] (a simple proof may be
obtained with the help of the theory of generalized functions [15], see section 10) other solutions
of (30) do not exist. This theorem shows that the ’combined limit’ cannot be performed for all
potentials. Although the present treatment does not cover all conceivable physical situations, the results
obtained so far imply already definitively that the limit 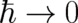 of QT does not agree with
NM.
of QT does not agree with
NM.