8 Discussion
In our first limiting procedure, which is appropriate for ’well-behaved’ quantum states, we found that QT agrees
in the limit 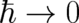 with a classical statistical theory referred to as PHJ. The latter contains as a limiting
case the deterministic states ruled by NM. Let us stress once again that the fact that these deterministic
states are ’contained’ in QT does not mean that NM is the limit of QT. This limit is PHJ which
contains a much larger number of (probabilistic) states not belonging to NM. In a second attempt
the limit
with a classical statistical theory referred to as PHJ. The latter contains as a limiting
case the deterministic states ruled by NM. Let us stress once again that the fact that these deterministic
states are ’contained’ in QT does not mean that NM is the limit of QT. This limit is PHJ which
contains a much larger number of (probabilistic) states not belonging to NM. In a second attempt
the limit 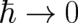 was simultaneously performed in the wave-packet width and in the basic
equations. We found that almost all states do not admit a transition from QT to NM in the limit
was simultaneously performed in the wave-packet width and in the basic
equations. We found that almost all states do not admit a transition from QT to NM in the limit
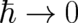 .
.
Our final result is then that NM is not the limit 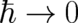 of QT. This result has been obtained in the
framework of standard QT using the Schrödinger picture to describe the quantum dynamics. One may ask
whether this conclusion is specific for these choices, or remains true for other dynamical pictures, such as e.g. the
Heisenberg picture, and other formulations of QT, such as e.g. Feynman’s path-integral formulation. Recall that
the present approach is (as discussed in 1) solely based on predictions i.e. the numerical output of the quantum
theoretical formalism. These numbers do not depend on a particular picture of quantum dynamics. They are also
independent from the choice of a particular formulation of QT since all formulations of QT must lead to the
same predictions.
of QT. This result has been obtained in the
framework of standard QT using the Schrödinger picture to describe the quantum dynamics. One may ask
whether this conclusion is specific for these choices, or remains true for other dynamical pictures, such as e.g. the
Heisenberg picture, and other formulations of QT, such as e.g. Feynman’s path-integral formulation. Recall that
the present approach is (as discussed in 1) solely based on predictions i.e. the numerical output of the quantum
theoretical formalism. These numbers do not depend on a particular picture of quantum dynamics. They are also
independent from the choice of a particular formulation of QT since all formulations of QT must lead to the
same predictions.
Let us illustrate the last point by a discussion of the path-integral formulation of QT [?]. The central quantity of
this approach, the propagator, is an infinite sum of terms of the form 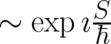 , where
, where
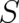 is the classical action and each term in the sum is to be evaluated at a different path between
the initial and final space-time points
is the classical action and each term in the sum is to be evaluated at a different path between
the initial and final space-time points 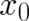 and
and 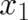 . In the classical limit
. In the classical limit 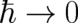 the
dominating contribution to the sum comes from the classical path between
the
dominating contribution to the sum comes from the classical path between 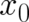 and
and 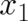 , which
extremizes
, which
extremizes 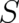 . The fact that this path obeys the differential equations (2) of NM is sometimes
interpreted in the sense of a transition from QT to NM, which the path-integral formulation reveals in
a particular rigourous and straighforward way. Such an interpretation is not justified. The form
of the propagator says nothing about the fact whether or not a particle is really present at the
initial space-time point
. The fact that this path obeys the differential equations (2) of NM is sometimes
interpreted in the sense of a transition from QT to NM, which the path-integral formulation reveals in
a particular rigourous and straighforward way. Such an interpretation is not justified. The form
of the propagator says nothing about the fact whether or not a particle is really present at the
initial space-time point 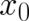 ; it tells us just what will happen given that a particle occupies the
point
; it tells us just what will happen given that a particle occupies the
point 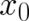 with certainty. The second variable of QT, the probability density
with certainty. The second variable of QT, the probability density 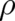 , must also
be taken into account; it enters the initial state and makes the final state uncertain despite the
’deterministic’ form of the propagator. A general classification scheme for probabilistic theories, taking the
different roles of initial values and evolution equations into account, has been reported recently [12].
It is a general feature of classical statistical theories that the time-evolution in the event space
(configuration or phase space) is deterministic and the impossibility to make deterministic predictions
(on single events) is solely due to uncertainty in the initial values. This classical feature is also
visible in the phase-space theory (5) and (though in a less explicit way) in the configuration-space
theory PHJ [see (8) and (10)]. It is this feature, and not the transition from QT to NM, which is
most explicit in the path-integral formalism. The classical limit of Feynman’s version of QT is
equivalent to the classical limit of Schrödinger’s version of QT (the PHJ) since both versions are
equivalent.
, must also
be taken into account; it enters the initial state and makes the final state uncertain despite the
’deterministic’ form of the propagator. A general classification scheme for probabilistic theories, taking the
different roles of initial values and evolution equations into account, has been reported recently [12].
It is a general feature of classical statistical theories that the time-evolution in the event space
(configuration or phase space) is deterministic and the impossibility to make deterministic predictions
(on single events) is solely due to uncertainty in the initial values. This classical feature is also
visible in the phase-space theory (5) and (though in a less explicit way) in the configuration-space
theory PHJ [see (8) and (10)]. It is this feature, and not the transition from QT to NM, which is
most explicit in the path-integral formalism. The classical limit of Feynman’s version of QT is
equivalent to the classical limit of Schrödinger’s version of QT (the PHJ) since both versions are
equivalent.
Our final result, the fact that NM is not the limit 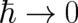 of QT, is in disagreement with Dirac’s
statement quoted at the beginning of our study. Dirac discusses the problem of the classical limit in section 31 of
his book. He formulates the following general principle:
of QT, is in disagreement with Dirac’s
statement quoted at the beginning of our study. Dirac discusses the problem of the classical limit in section 31 of
his book. He formulates the following general principle:
For any dynamical system with a classical analogue, a state for which the classical description
is valid as an approximation is presented in quantum mechanics as a wave packet,...so in
order that the classical description be valid, the wave packet should remain a wave packet
and should move according to the laws of classical dynamics. We shall verify that this is so.
The following calculation is intended to show that such a wave packet always exists. Unfortunately, a systematic
investigation of different classes of potentials or initial values is not performed. Instead, Dirac imposes several
conditions for the considered wave packets, formulated verbally or in the form of inequalities, which he assumes
to be true for arbitrary potentials but which need not necessarily be true. He arrives at the canonical equations
of motions for the peaks of supposedly arbitrary wave packets. In reality, these conditions impose strong
restrictions on the form of initial values and potentials and can only be fulfilled in few very special
cases. Quantum-mechanical solutions for the three ’deterministic potentials’, where Ehrenfest’s
relations agree with NM, are often used to demonstrate ’classical behavior’ of wave packets. It
should be borne in mind that this behavior is not generic but represents the exception(s) from the
rule.
After the discovery of QT the community was shocked by the breakdown of NM in the microscopic
world and it seemed inconceivable that NM should not even survive as the classical limit of QT.
Schrödinger, like Dirac, considered it as evident, and wrote at the end of his famous paper about coherent
states [22]:
We can definitely foresee that, in a similar way, wave groups can be constructed which move
round highly quantized Kepler ellipses and are the representation by wave mechanics of the
hydrogen electron.
The coherent states of the harmonic oscillator have been generalized to arbitrary potentials in various ways [26]
but none of these generalizations admits a clear transition to the classical (deterministic) limit. Special attention
was, of course, devoted to the Coulomb potential, but despite intense research, Schrödinger’s idea could not be
realized and this chapter has apparently already been closed [27].
The classical limit of QT is the PHJ, a classical statistical theory defined by Eqs. (8), (9). The limit
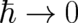 transforms a quantum probabilistic theory into a classical probabilistic theory. The behavior of
the uncertainty relation illustrates this conclusion in a simple way. For
transforms a quantum probabilistic theory into a classical probabilistic theory. The behavior of
the uncertainty relation illustrates this conclusion in a simple way. For 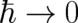 it takes the
form
it takes the
form
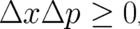 | (31) |
which means that in the classical limit the uncertainty product is in general different from zero; a detailed
comparison has been reported by Devi and Karthik [4]. Almost all states of PHJ will show uncertainties; the
equality sign in (31) just indicates that the transition to the deterministic limit (as performed in section 4) is
not forbidden.
The classical limit plays an important role in the prolonged discussion about the proper interpretation of QT. In
the years after discovery of QT a number of dogmas have been established, which have been repeated since then
so many times that they are considered today as ’well-established’ scientific facts. One of these dogmas states
that ”QT provides a complete description of individual particles”. It is hard to understand how a probabilistic
theory could provide a ’complete’ description of individual events. But one should first analyze the possible
meanings of the term ’complete’. A detailed analysis shows that this term is ambiguous [?]. It may mean
’no better theory exists’ (metaphysical completeness) or ’all facts that can be observed can be
predicted’ (predictive completeness). The still prevailing (Copenhagen) standard interpretation
claims that QT is complete in both respects. Einstein, Podolsky, and Rosen (EPR), showed that QT
is predictive incomplete [7]. In the last paragraph of their paper [7], the authors expressed their
belief that QT is metaphysical incomplete. EPR’s proof of predictive incompleteness was correct
and could not be attacked, so metaphysical incompleteness was attacked instead. The EPR paper
was misinterpreted as if the authors had claimed they had proven metaphysical incompleteness.
Further consequences of this misinterpretation will not be discussed here. The important point to
note is that metaphysical completeness is a philosophical term; physics can only test predictive
completeness (by comparison with observation). Thus, let us concentrate on the question of predictive
completeness of QT; in the remaining part of this section the term completeness will be used in this
sense.
The fact that NM disagrees with the 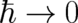 limit of QT presents a painful obstacle to the completeness
dogma. Every statistical theory, no matter whether classical or quantum, is unable to predict individual events
and is therefore, by its very definition, incomplete. How can quantum theory be complete if its classical limit is
incomplete? In order to eliminate this problem, Bohr created the ’correspondence principle’. It postulates, that
quantum states become similar to states of NM for large values of
limit of QT presents a painful obstacle to the completeness
dogma. Every statistical theory, no matter whether classical or quantum, is unable to predict individual events
and is therefore, by its very definition, incomplete. How can quantum theory be complete if its classical limit is
incomplete? In order to eliminate this problem, Bohr created the ’correspondence principle’. It postulates, that
quantum states become similar to states of NM for large values of 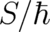 . However, this principle is not in
agreement with the structure of Schrödinger’s equation. For large
. However, this principle is not in
agreement with the structure of Schrödinger’s equation. For large 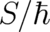 the quantum term in Eq (9)
becomes negligibly small and QT becomes similar to PHJ and not to NM; similarity with NM
requires in addition a sharply-peaked
the quantum term in Eq (9)
becomes negligibly small and QT becomes similar to PHJ and not to NM; similarity with NM
requires in addition a sharply-peaked 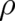 . The breakdown of Bohr’s correspondence principle in
concrete situations has been reported many times in the literature; see e.g. Cabrera and Kiwi [2] and
Diamond [5].
. The breakdown of Bohr’s correspondence principle in
concrete situations has been reported many times in the literature; see e.g. Cabrera and Kiwi [2] and
Diamond [5].
What might our bright student - whose incisive question has triggered this investigation - say at this
point (if he is still listening) ? Maybe he says ”O.K, so far. But is not my reasoning necessarily
correct, even without reference to Dirac’s statement ?”. Again, one can imagine a variety of possible
answers. From the point of view of the present author, the answer is: ”Nothing is wrong with your
reasoning; considered as a logical implication it is perfectly correct. But the conclusion need not be
true because the premise is wrong: QT does not describe a single electron nor does it describe
any other single particle; it is a statistical theory whose predictions refer to statistical ensembles
only”.
 with a classical statistical theory referred to as PHJ. The latter contains as a limiting
case the deterministic states ruled by NM. Let us stress once again that the fact that these deterministic
states are ’contained’ in QT does not mean that NM is the limit of QT. This limit is PHJ which
contains a much larger number of (probabilistic) states not belonging to NM. In a second attempt
the limit
with a classical statistical theory referred to as PHJ. The latter contains as a limiting
case the deterministic states ruled by NM. Let us stress once again that the fact that these deterministic
states are ’contained’ in QT does not mean that NM is the limit of QT. This limit is PHJ which
contains a much larger number of (probabilistic) states not belonging to NM. In a second attempt
the limit 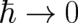 was simultaneously performed in the wave-packet width and in the basic
equations. We found that almost all states do not admit a transition from QT to NM in the limit
was simultaneously performed in the wave-packet width and in the basic
equations. We found that almost all states do not admit a transition from QT to NM in the limit
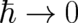 .
.
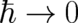 of QT. This result has been obtained in the
framework of standard QT using the Schrödinger picture to describe the quantum dynamics. One may ask
whether this conclusion is specific for these choices, or remains true for other dynamical pictures, such as e.g. the
Heisenberg picture, and other formulations of QT, such as e.g. Feynman’s path-integral formulation. Recall that
the present approach is (as discussed in
of QT. This result has been obtained in the
framework of standard QT using the Schrödinger picture to describe the quantum dynamics. One may ask
whether this conclusion is specific for these choices, or remains true for other dynamical pictures, such as e.g. the
Heisenberg picture, and other formulations of QT, such as e.g. Feynman’s path-integral formulation. Recall that
the present approach is (as discussed in 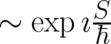 , where
, where
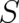 is the classical action and each term in the sum is to be evaluated at a different path between
the initial and final space-time points
is the classical action and each term in the sum is to be evaluated at a different path between
the initial and final space-time points 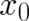 and
and 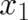 . In the classical limit
. In the classical limit 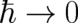 the
dominating contribution to the sum comes from the classical path between
the
dominating contribution to the sum comes from the classical path between 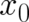 and
and 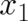 , which
extremizes
, which
extremizes 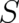 . The fact that this path obeys the differential equations (
. The fact that this path obeys the differential equations (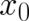 ; it tells us just what will happen
; it tells us just what will happen 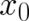 with certainty. The second variable of QT, the probability density
with certainty. The second variable of QT, the probability density 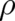 , must also
be taken into account; it enters the initial state and makes the final state uncertain despite the
’deterministic’ form of the propagator. A general classification scheme for probabilistic theories, taking the
different roles of initial values and evolution equations into account, has been reported recently
, must also
be taken into account; it enters the initial state and makes the final state uncertain despite the
’deterministic’ form of the propagator. A general classification scheme for probabilistic theories, taking the
different roles of initial values and evolution equations into account, has been reported recently 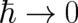 of QT, is in disagreement with Dirac’s
statement quoted at the beginning of our study. Dirac discusses the problem of the classical limit in section 31 of
his book. He formulates the following general principle:
of QT, is in disagreement with Dirac’s
statement quoted at the beginning of our study. Dirac discusses the problem of the classical limit in section 31 of
his book. He formulates the following general principle:
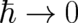 transforms a quantum probabilistic theory into a classical probabilistic theory. The behavior of
the uncertainty relation illustrates this conclusion in a simple way. For
transforms a quantum probabilistic theory into a classical probabilistic theory. The behavior of
the uncertainty relation illustrates this conclusion in a simple way. For 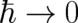 it takes the
form
it takes the
form
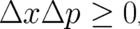
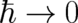 limit of QT presents a painful obstacle to the completeness
dogma. Every statistical theory, no matter whether classical or quantum, is unable to predict individual events
and is therefore, by its very definition, incomplete. How can quantum theory be complete if its classical limit is
incomplete? In order to eliminate this problem, Bohr created the ’correspondence principle’. It postulates, that
quantum states become similar to states of NM for large values of
limit of QT presents a painful obstacle to the completeness
dogma. Every statistical theory, no matter whether classical or quantum, is unable to predict individual events
and is therefore, by its very definition, incomplete. How can quantum theory be complete if its classical limit is
incomplete? In order to eliminate this problem, Bohr created the ’correspondence principle’. It postulates, that
quantum states become similar to states of NM for large values of 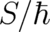 . However, this principle is not in
agreement with the structure of Schrödinger’s equation. For large
. However, this principle is not in
agreement with the structure of Schrödinger’s equation. For large 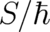 the quantum term in Eq (
the quantum term in Eq (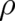 . The breakdown of Bohr’s correspondence principle in
concrete situations has been reported many times in the literature; see e.g. Cabrera and Kiwi
. The breakdown of Bohr’s correspondence principle in
concrete situations has been reported many times in the literature; see e.g. Cabrera and Kiwi