
Albert Einstein (1949)
Source: From Albert Einstein: Philosopher-Scientist (1949), from The Library of Living Philosophers Series;
Published: by Cambridge University Press,
1949. Including Neils Bohr's report of conversations with Einstein and
Einstein's, reply reproduced here.

BY WAY of introduction I must remark that it was not easy for me to do justice to the task of expressing myself concerning the essays contained in this volume. The reason lies in the fact that the essays refer to entirely too many subjects, which, at the present state of our knowledge, are only loosely connected with each other. I first attempted to discuss the essays individually. However, I abandoned this procedure because nothing even approximately homogeneous resulted, so that the reading of it could hardly have been either useful or enjoyable. I finally decided, therefore, to order these remarks, as far as possible, according to topical considerations.
Furthermore, after some vain efforts, I discovered that the mentality which underlies a few of the essays differs so radically from my own, that I am incapable of saying anything useful about them. This is not to be interpreted that I regard those essays - insofar as their content is at all meaningful to me - less highly than I do those which lie closer to my own ways of thinking, to which [latter] I dedicate the following remarks.
To begin with I refer to the essays of Wolfgang Pauli and Max Born. They describe the content of my work concerning quanta and statistics in general in their inner consistency and in their participation in the evolution of physics during the last half century. It is meritorious that they have done this: For only those who have successfully wrestled with the problematic situations of their own age can have a deep insight into those situations; unlike the later historian, who finds it difficult to make abstractions from those concepts and views which appear to his generation as established, or even as self-evident. Both authors deprecate the fact that I reject the basic idea of contemporary statistical quantum theory, insofar as I do not believe that this fundamental concept will provide a useful basis for the whole of physics. More of this later.
I now come to what is probably the most interesting subject which absolutely must be discussed in connection with the detailed arguments of my highly esteemed colleagues Born, Pauli, Heitler, Bohr, and Margenau. They are all firmly convinced that the riddle of the double nature of all corpuscles (corpuscular and undulatory character) has in essence found its final solution in the statistical quantum theory. On the strength of the successes of this theory they consider it proved that a theoretically complete description of a system can, in essence, involve only statistical assertions concerning the measurable quantities of this system. They are apparently all of the opinion that Heisenberg's indeterminacy-relation (the correctness of which is, from my own point of view, rightfully regarded as finally demonstrated) is essentially prejudicial in favour of the character of all thinkable reasonable physical theories in the mentioned sense. In what follows I wish to adduce reasons which keep me from falling in line with the opinion of almost all contemporary theoretical physicists. I am, in fact, firmly convinced that the essentially statistical character of contemporary quantum theory is solely to be ascribed to the fact that this [theory] operates with an incomplete description of physical systems.
Above all, however, the reader should be convinced that I fully recognise the very important progress which the statistical quantum theory has brought to theoretical physics. In the field of mechanical problems - i.e., wherever it is possible to consider the interaction of structures and of their parts with sufficient accuracy by postulating a potential energy between material points - [this theory] even now presents a system which, in its closed character, correctly describes the empirical relations between statable phenomena as they were theoretically to be expected. This theory is until now the only one which unites the corpuscular and undulatory dual character of matter in a logically satisfactory fashion; and the (testable) relations, which are contained in it, are, within the natural limits fixed by the indeterminacy-relation, complete. The formal relations which are given in this theory - i.e., its entire mathematical formalism - will probably have to be contained, in the form of logical inferences, in every useful future theory.
What does not satisfy me in that theory, from the standpoint of principle, is its attitude towards that which appears to me to be the programmatic aim of all physics: the complete description of any (individual) real situation (as it supposedly exists irrespective of any act of observation or substantiation). Whenever the positivistically inclined modern physicist hears such a formulation his reaction is that of a pitying smile. He says to himself: "there we have the naked formulation of a metaphysical prejudice, empty of content, a prejudice, moreover, the conquest of which constitutes the major epistemological achievement of physicists within the last quarter-century. Has any man ever perceived a 'real physical situation'? How is it possible that a reasonable person could today still believe that he can refute our essential knowledge and understanding by drawing up such a bloodless ghost?" Patience! The above laconic characterisation was not meant to convince anyone; it was merely to indicate the point of view around which the following elementary considerations freely group themselves. In doing this I shall proceed as follows: I shall first of all show in simple special cases what seems essential to me, and then I shall make a few remarks about some more general ideas which are involved.
We consider as a physical system, in the first instance, a radioactive atom of definite average decay time, which is practically exactly localised at a point of the coordinate system. The radioactive process consists in the emission of a (comparatively light) particle. For the sake of simplicity we neglect the motion of the residual atom after the disintegration process. Then it is possible for us, following Gamow, to replace the rest of the atom by a space of atomic order of magnitude, surrounded by a closed potential energy barrier which, at a time t = 0, encloses the particle to be emitted. The radioactive process thus schematised is then, as is well known, to be described - in the sense of elementary quantum mechanics - by a Psi-function in three dimensions, which at the time t= 0 is different from zero only inside of the barrier, but which, for positive times, expands into the outer space. This Psi-function yields the probability that the particle, at some chosen instant, is actually in a chosen part of space (i.e., is actually found there by a measurement of position). On the other hand, the Psi-function does not imply any assertion concerning the time instant of the disintegration of the radioactive atom.
Now we raise the question: Can this theoretical description be taken as the complete description of the disintegration of a single individual atom? The immediately plausible answer is: No. For one is, first of all, inclined to assume that the individual atom decays at a definite time; however, such a definite time-value is not implied in the description by the Psi-function. If, therefore, the individual atom has a definite disintegration time, then as regards the individual atom its description by means of the Psi-function must be interpreted as an incomplete description. In this case the Psi-function is to be taken as the description, not of a singular system, but of an ideal ensemble of systems. In this case one is driven to the conviction that a complete description of a single system should, after all, be possible, but for such complete description there is no room in the conceptual world of statistical quantum theory.
To this the quantum theorist will reply: This consideration stands and falls with the assertion that there actually is such a thing as a definite time of disintegration of the individual atom (an instant of time existing independently of any observation). But this assertion is, from my point of view, not merely arbitrary but actually meaningless. The assertion of the existence of a definite time-instant for the disintegration makes sense only if I can in principle determine this time-instant empirically. Such an assertion, however, (which, finally, leads to the attempt to prove the existence of the particle outside of the force barrier), involves a definite disturbance of the system in which we are interested, so that the result of the determination does not permit a conclusion concerning the status of the undisturbed system. The supposition, therefore, that a radioactive atom has a definite disintegration-time is not justified by anything whatsoever; it is, therefore, not demonstrated either that the Psi-function can not be conceived as a complete description of the individual system. The entire alleged difficulty proceeds from the fact that one postulates something not observable as "real." (This the answer of the quantum theorist.)
What I dislike in this kind of argumentation is the basic positivistic attitude, which from my point of view is untenable, and which seems to me to come to the same thing as Berkeley's principle, esse est percipi. "Being" is always something which is mentally constructed by us, that is, something which we freely posit (in the logical sense). The justification of such constructs does not lie in their derivation from what is given by the senses. Such a type of derivation (in the sense of logical deducibility) is nowhere to be had, not even in the domain of pre-scientific thinking. The justification of the constructs, which represent "reality" for us, lies alone in their quality of making intelligible what is sensorily given (the vague character of this expression is here forced upon me by my striving for brevity). Applied to the specifically chosen example this consideration tells us the following:
One may not merely ask: "Does a definite time instant for the transformation of a single atom exist?" but rather: "Is it, within the framework of our theoretical total construction, reasonable to posit the existence of a definite point of time for the transformation of a single atom?" One may not even ask what this assertion means. One can only ask whether such a proposition, within the framework of the chosen conceptual system - with a view to its ability to grasp theoretically what is empirically given - is reasonable or not.
Insofar, then, as a quantum-theoretician takes the position that the description by means of a Psi-function refers only to an ideal systematic totality but in no wise to the individual system, he may calmly assume a definite point of time for the transformation. But, if he represents the assumption that his description by way of the Psi-function is to be taken as the complete description of the individual system, then he must reject the postulation of a specific decay-time. He can justifiably point to the fact that a determination of the instant of disintegration is not possible on an isolated system, but would require disturbances of such a character that they must not be neglected in the critical examination of the situation. It would, for example, not be possible to conclude from the empirical statement that the transformation has already taken place, that this would have been the case if the disturbances of the system had not taken place.
As far as I know, it was E. Schrödinger who first called attention to a modification of this consideration, which shows an interpretation of this type to be impracticable. Rather than considering a system which comprises only a radioactive atom (and its process of transformation), one considers a system which includes also the means for ascertaining the radioactive transformation - for example, a Geiger-counter with automatic registration-mechanism. Let this latter include a registration-strip, moved by a clockwork, upon which a mark is made by tripping the counter. True, from the point of view of quantum mechanics this total system is very complex and its configuration space is of very high dimension. But there is in principle no objection to treating this entire system from the standpoint of quantum mechanics. Here too the theory determines the probability of each configuration of all its co-ordinates for every time instant. If one considers all configurations of the coordinates, for a time large compared with the average decay time of the radioactive atom, there will be (at most) one such registration-mark on the paper strip. To each coordinate configuration corresponds a definite position of the mark on the paper strip. But, inasmuch as the theory yields only the relative probability of the thinkable co-ordinate-configurations, it also offers only relative probabilities for the positions of the mark on the paper strip, but no definite location for this mark.
In this consideration the location of the mark on the strip plays the role played in the original consideration by the time of the disintegration. The reason for the introduction of the system supplemented by the registration-mechanism lies in the following. The location of the mark on the registration-strip is a fact which belongs entirely within the sphere of macroscopic concepts, in contradistinction to the instant of disintegration of a single atom. If we attempt [to work with] the interpretation that the quantum-theoretical description is to be understood as a complete description of the individual system, we are forced to the interpretation that the location of the mark on the strip is nothing which belongs to the system per se, but that the existence of that location is essentially dependent upon the carrying out of an observation made on the registration-strip. Such an interpretation is certainly by no means absurd from a purely logical standpoint, yet there is hardly likely to be anyone who would be inclined to consider it seriously. For, in the macroscopic sphere it simply is considered certain that one must adhere to the program of a realistic description in space and time; whereas in the sphere of microscopic situations one is more readily inclined to give up, or at least to modify, this program.
This discussion was only to bring out the following. One arrives at very implausible theoretical conceptions, if one attempts to maintain the thesis that the statistical quantum theory is in principle capable of producing a complete description of an individual physical system. On the other hand, those difficulties of theoretical interpretation disappear, if one views the quantum-mechanical description as the description of ensembles of systems.
I reached this conclusion as the result of quite different types of considerations. I am convinced that everyone who will take the trouble to carry through such reflections conscientiously will find himself finally driven to this interpretation of quantum-theoretical description (the Psi-function is to be understood as the description not of a single system but of an ensemble of systems).
Roughly stated the conclusion is this: Within the framework of statistical quantum theory there is no such thing as a complete description of the individual system. More cautiously it might be put as follows: The attempt to conceive the quantum-theoretical description as the complete description of the individual systems leads to unnatural theoretical interpretations, which become immediately unnecessary if one accepts the interpretation that the description refers to ensembles of systems and not to individual systems. In that case the whole "egg-walking" performed in order to avoid the "physically real" becomes superfluous. There exists, however, a simple psychological reason for the fact that this most nearly obvious interpretation is being shunned. For if the statistical quantum theory does not pretend to describe the individual system (and its development in time) completely, it appears unavoidable to look elsewhere for a complete description of the individual system; in doing so it would be clear from the very beginning that the elements of such a description are not contained within the conceptual scheme of the statistical quantum theory. With this one would admit that, in principle, this scheme could not serve as the basis of theoretical physics. Assuming the success of efforts to accomplish a complete physical description, the statistical quantum theory would, within the framework of future physics, take an approximately analogous position to the statistical mechanics within the framework of classical mechanics. I am rather firmly convinced that the development of theoretical physics will be of this type; but the path will be lengthy and difficult.
I now imagine a quantum theoretician who may even admit that the quantum-theoretical description refers to ensembles of systems and not to individual systems, but who, nevertheless, clings to the idea that the type of description of the statistical quantum theory will, in its essential features, be retained in the future. He may argue as follows: True, I admit that the quantum-theoretical description is an incomplete description of the individual system. I even admit that a complete theoretical description is, in principle, thinkable. But I consider it proven that the search for such a complete description would be aimless. For the lawfulness of nature is thus constituted that the laws can be completely and suitably formulated within the framework of our incomplete description.
To this I can only reply as follows: Your point of view - taken as theoretical possibility - is incontestable. For me, however, the expectation that the adequate formulation of the universal laws involves the use of all conceptual elements which are necessary for a complete description, is more natural. It is furthermore not at all surprising that, by using an incomplete description, (in the main) only statistical statements can be obtained out of such description. If it should be possible to move forward to a complete description, it is likely that the laws would represent relations among all the conceptual elements of this description which, per se, have nothing to do with statistics.
A few more remarks of a general nature concerning concepts and [also] concerning the insinuation that a concept - for example that of the real - is something metaphysical (and therefore to be rejected). A basic conceptual distinction, which is a necessary prerequisite of scientific and pre-scientific thinking, is the distinction between "sense-impressions" (and the recollection of such) on the one hand and mere ideas on the other. There is no such thing as a conceptual definition of this distinction (aside from, circular definitions, i.e., of such as make a hidden use of the object to be defined). Nor can it be maintained that at the base of this distinction there is a type of evidence, such as underlies, for example, the distinction between red and blue. Yet, one needs this distinction in order to be able to overcome solipsism. Solution: we shall make use of this distinction unconcerned with the reproach that, in doing so, we are guilty of the metaphysical "original sin." We regard the distinction as a category which we use in order that we might the better find our way in the world of immediate sensations. The "sense" and the justification of this distinction lies simply in this achievement. But this is only a first step. We represent the sense-impressions as conditioned by an "objective" and by a "subjective" factor. For this conceptual distinction there also is no logical-philosophical justification. But if we reject it, we cannot escape solipsism. It is also the presupposition of every kind of physical thinking. Here too, the only justification lies in its usefulness. We are here concerned with "categories" or schemes of thought, the selection of which is, in principle, entirely open to us and whose qualification can only be judged by the degree to which its use contributes to making the totality of the contents of consciousness "intelligible." The above mentioned "objective factor" is the totality of such concepts and conceptual relations as are thought of as independent of experience, viz., of perceptions. So long as we move within the thus programmatically fixed sphere of thought we are thinking physically. Insofar as physical thinking justifies itself, in the more than once indicated sense, by its ability to grasp experiences intellectually, we regard it as "knowledge of the real."
After what has been said, the "real" in physics is to be taken as a type of program, to which we are, however, not forced to cling a priori. No one is likely to be inclined to attempt to give up this program within the realm of the "macroscopic" (location of the mark on the paper strip "real"). But the "macroscopic" and the "microscopic" are so inter-related that it appears impracticable to give up this program in the "microscopic" alone. Nor can I see any occasion anywhere within the observable facts of the quantum-field for doing so, unless, indeed, one clings a priori to the thesis that the description of nature by the statistical scheme of quantum-mechanics is final.
The theoretical attitude here advocated is distinct from that of Kant only by the fact that we do not conceive of the "categories" as unalterable (conditioned by the nature of the understanding) but as (in the logical sense) free conventions. They appear to be a priori only insofar as thinking without the positing of categories and of concepts in general would be as impossible as is breathing in a vacuum.
From these meagre remarks one will see that to me it must seem a mistake to permit theoretical description to be directly dependent upon acts of empirical assertions, as it seems to me to be intended [for example] in Bohr's principle of complementarity, the sharp formulation of which, moreover, I have been unable to achieve despite much effort which I have expended on it. From my point of view [such] statements or measurements can occur only as special instances, viz., parts, of physical description, to which I cannot ascribe any exceptional position above the rest.
The above mentioned essays by Bohr and Pauli contain a historical appreciation of my efforts in the area of physical statistics and quanta and, in addition, an accusation which is brought forward in the friendliest of fashion. In briefest formulation this latter runs as follows: "Rigid adherence to classical theory." This accusation demands either a defence or the confession of guilt. The one or the other is, however, being rendered much more difficult because it is by no means immediately clear what is meant by "classical theory." Newton's theory deserves the name of a classical theory. It has nevertheless been abandoned since Maxwell and Hertz have shown that the idea of forces at a distance has to be relinquished and that one cannot manage without the idea of continuous "fields." The opinion that continuous fields are to be viewed as the only acceptable basic concepts, which must also be assumed to underlie the theory of the material particles, soon won out. Now this conception became, so to speak, "classical;" but a proper, and in principle complete, theory has not grown out of it. Maxwell's theory of the electric field remained a torso, because it was unable to set up laws for the behaviour of electric density, without which there can, of course, be no such thing as an electro-magnetic field. Analogously the general theory of relativity furnished then a field theory of gravitation, but no theory of the field-creating masses. (These remarks presuppose it as self-evident that a field-theory may not contain any singularities, i.e., any positions or parts in space in which the field laws are not valid.)
Consequently there is, strictly speaking, today no such thing as a classical field-theory; one can, therefore, also not rigidly adhere to it. Nevertheless, field-theory does exist as a program: "Continuous functions in the four-dimensional [continuum] as basic concepts of the theory." Rigid adherence to this program can rightfully be asserted of me. The deeper ground for this lies in the following: The theory of gravitation showed me that the non-linearity of these equations results in the fact that this theory yields interactions among structures (localised things) at all. But the theoretical search for non-linear equations is hopeless (because of too great variety of possibilities), if one does not use the general principle of relativity (invariance under general continuous co-ordinate-transformations). In the meantime, however, it does not seem possible to formulate this principle, if one seeks to deviate from the above program. Herein lies a coercion which I cannot evade. This for my justification.
Nevertheless I am forced to weaken this justification by a confession. If one disregards quantum structure, one can justify the introduction of the gik "operationally" by pointing to the fact that one can hardly doubt the physical reality of the elementary light cone which belongs to a point. In doing so one implicitly makes use of the existence of an arbitrarily sharp optical signal. Such a signal, however, as regards the quantum facts, involves infinitely high frequencies and energies, and therefore a complete destruction of the field to be determined. That kind of a physical justification for the introduction of the gik falls by the wayside, unless one limits himself to the "macroscopic." The application of the formal basis of the general theory of relativity to the "microscopic" can, therefore, be based only upon the fact that that tensor is the formally simplest covariant structure which can come under consideration. Such argumentation, however, carries no weight with anyone who doubts that we have to adhere to the continuum at all. All honour to his doubt - but where else is there a passable road?
Now I come to the theme of the relation of the theory of relativity to philosophy. Here it is Reichenbach's piece of work which, by the precision of deductions and by the sharpness of his assertions, irresistibly invites a brief commentary. Robertson's lucid discussion also is interesting mainly from the standpoint of general epistemology, although it limits itself to the narrower theme of "the theory of relativity and geometry." To the question: Do you consider true what Reichenbach has here asserted, I can answer only with Pilate's famous question: "What is truth?"
Let us first take a good look at the question: Is a geometry - looked at from the physical point of view - verifiable (viz., falsifiable) or not? Reichenbach, together with Helmholtz, says: Yes, provided that the empirically given solid body realises the concept of "distance." Poincare says no and consequently is condemned by Reichenbach. Now the following short conversation takes place:
Poincare: The empirically given bodies are not rigid, and consequently can not be used for the embodiment of geometric intervals. Therefore, the theorems of geometry are not verifiable.
Reichenbach: I admit that there are no bodies which can be immediately adduced for the "real definition" of the interval. Nevertheless, this real definition can be achieved by taking the thermal volume-dependence, elasticity, electro- and magnetostriction, etc., into consideration. That this is really [and] without contradiction possible, classical physics has surely demonstrated.
Poincare: In gaining the real definition improved by yourself you have made use of physical laws, the formulation of which presupposes (in this case) Euclidean geometry. The verification, of which you have spoken, refers, therefore, not merely to geometry but to the entire system of physical laws which constitute its foundation. An examination of geometry by itself is consequently not thinkable. - Why should it consequently not be entirely up to me to choose geometry according to my own convenience (i.e., Euclidean) and to fit the remaining (in the usual sense "physical") laws to this choice in such manner that there can arise no contradiction of the whole with experience?
(The conversation cannot be continued in this fashion because the respect of the [present] writer for Poincare's superiority as thinker and author does not permit it; in what follows therefore, an anonymous non-positivist is substituted for Poincare. - )
Reichenbach: There is something quite attractive in this conception. But, on the other hand, it is noteworthy that the adherence to the objective meaning of length and to the interpretation of the differences of co-ordinates as distances (in pre-relativistic physics) has not led to complications. Should we not, on the basis of this astounding fact, be justified in operating further at least tentatively with the concept of the measurable length, as if there were such things as rigid measuring-rods. In any case it would have been impossible for Einstein de facto (even if not theoretically) to set up the theory of general relativity, if he had not adhered to the objective meaning of length.
Against Poincare's suggestion it is to be pointed out that what really matters is not merely the greatest possible simplicity of the geometry alone, but rather the greatest possible simplicity of all of physics (inclusive of geometry). This is what is, in the first instance, involved in the fact that today we must decline as unsuitable the suggestion to adhere to Euclidean geometry.
Non-Positivist: If, under the stated circumstances, you hold distance to be a legitimate concept, how then is it with your basic principle (meaning = verifiability) ? Do you not have to reach the point where you must deny the meaning of geometrical concepts and theorems and to acknowledge meaning only within the completely developed theory of relativity (which, however, does not yet exist at all as a finished product)? Do you not have to admit that, in your sense of the word, no "meaning" can be attributed to the individual concepts and assertions of a physical theory at all, and to the entire system only insofar as it makes what is given in experience "intelligible?" Why do the individual concepts which occur in a theory require any specific Justification anyway, if they are only indispensable within the framework of the logical structure of the theory, and the theory only in its entirety validates itself?
It seems to me, moreover, that you have not at all done justice to the really significant philosophical achievement of Kant. From Hume Kant had learned that there are concepts (as, for example, that of causal connection), which play a dominating role in our thinking, and which, nevertheless, can not be deduced by means of a logical process from the empirically given (a fact which several empiricists recognise, it is true, but seem always again to forget). What justifies the use of such concepts? Suppose he had replied in this sense: Thinking is necessary in order to understand the empirically given, and concepts and "categories" are necessary as indispensable elements of thinking. If he had remained satisfied with this type of an answer, he would have avoided scepticism and you would not have been able to find fault with him. He, however, was misled by the erroneous opinion, difficult to avoid in his time - that Euclidean geometry is necessary to thinking and offers assured (i.e., not dependent upon sensory experience) knowledge concerning the objects of "external" perception. From this easily understandable error he concluded the existence of synthetic judgments a priori, which are produced by the reason alone, and which, consequently, can lay claim to absolute validity. I think your censure is directed less against Kant himself than against those who today still adhere to the errors of "synthetic judgments a priori."
I can hardly think of anything more stimulating as the basis for discussion in an epistemological seminar than this brief essay by Reichenbach (best taken together with Robertson's essay).
What has been discussed thus far is closely related to Bridgman's essay, so that it will be possible for me to express myself quite briefly without having to harbour too much fear that I shall be misunderstood. In order to be able to consider a logical system as physical theory it is not necessary to demand that all of its assertions can be independently interpreted and "tested" "operationally;" de facto this has never yet been achieved by any theory and can not at all be achieved. In order to be able to consider a theory as a physical theory it is only necessary that it implies empirically testable assertions in general.
This formulation is insofar entirely unprecise as "testability" is a quality which refers not merely to the assertion itself but also to the co-ordination of concepts, contained in it, with experience. But it is probably hardly necessary for me to enter upon a discussion of this ticklish problem, inasmuch as it is not likely that there exist any essential differences of opinion at this point. -
Margenau;. This essay contains several original specific remarks, which I must consider separately:
To his Sec. I: "Einstein's position . . . contains features of rationalism and extreme empiricism...." This remark is entirely correct. From whence comes this fluctuation? A logical conceptual system is physics insofar as its concepts and assertions are necessarily brought into relationship with the world of experiences. Whoever desires to set up such a system will find a dangerous obstacle in arbitrary choice (embarras de richesse). This is why he seeks to connect his concepts as directly and necessarily as possible with the world of experience. In this case his attitude is empirical. This path is often fruitful, but it is always open to doubt, because the specific concept and the individual assertion can, after all, assert something confronted by the empirically given only in connection with the entire system. He then recognises that there exists no logical path from the empirically given to that conceptual world. His attitude becomes then more nearly rationalistic, because he recognises the logical independence of the system. The danger in this attitude lies in the fact that in the search for the system one can lose every contact with the world of experience. A wavering between these extremes appears to me unavoidable.
To his Sec. 2: I did not grow up in the Kantian tradition, but came to understand the truly valuable which is to be found in his doctrine, alongside of errors which today are quite obvious, only quite late. It is contained in the sentence: "The real is not given to us, but put to us (aufgegeben) (by way of a riddle)." This obviously means: There is such a thing as a conceptual construction for the grasping of the inter-personal, the authority of which lies purely in its validation. This conceptual construction refers precisely to the "real" (by definition), and every further question concerning the "nature of the real" appears empty.
To his Sec. 4: This discussion has not convinced me at all. For it is clear per se that every magnitude and every assertion of a theory lays claim to "objective meaning" (within the framework of the theory). A problem arises only when we ascribe group-characteristics to a theory, i.e., if we assume or postulate that the same physical situation admits of several ways of description, each of which is to be viewed as equally justified. For in this case we obviously cannot ascribe complete objective meaning (for example the x-component of the velocity of a particle or its x-coordinates) to the individual (not eliminable) magnitudes. In this case, which has always existed in physics, we have to limit ourselves to ascribing objective meaning to the general laws of the theory, i.e., we have to demand that these laws are valid for every description of the system which is recognised as justified by the group. It is, therefore, not true that "objectivity" presupposes a group-characteristic, but that the group-characteristic forces a refinement of the concept of objectivity. The positing of group characteristics is heuristically so important for theory, because this characteristic always considerably limits the variety of the mathematically meaningful laws.
Now there follows a claim that the group-characteristics determine that the laws must have the form of differential equations; I can not at all see this. Then Margenau insists that the laws expressed by way of the differential equations (especially the partial ones) are "least specific." Upon what does he base this contention? If they could be proved to be correct, it is true that the attempt to ground physics upon differential equations would then turn out to be hopeless. We are, however, far from being able to judge whether differential laws of the type to be considered have any solutions at all which are everywhere singularity-free; and, if so, whether there are too many such solutions.
And now just a remark concerning the discussions about the Einstein-Podolski-Rosen Paradox. I do not think that Margenau's defence of the "orthodox" ("orthodox" refers to the thesis that the t-function characterises the individual system exhaustively) quantum position hits the essential [aspects]. Of the "orthodox" quantum theoreticians whose position I know, Niels Bohr's seems to me to come nearest to doing justice to the problem. Translated into my own way of putting it, he argues as follows:
If the partial systems A and B form a total system which is described by its Psi-function Psi/(AB), there is no reason why any mutually independent existence (state of reality) should be ascribed to the partial systems A and B viewed separately, not even if the partial systems are spatially separated from each other at the particular time under consideration. The assertion that, in this latter case, the real situation of B could not be (directly) influenced by any measurement taken on A is, therefore, within the framework of quantum theory, unfounded and (as the paradox shows) unacceptable.
By this way of looking at the matter it becomes evident that the paradox forces us to relinquish one of the following two assertions:
(1) the description by means of the Psi-function is complete
(2) the real states of spatially separated objects are independent of each other.
On the other hand, it is possible to adhere to (2), if one regards the Psi-function as the description of a (statistical) ensemble of systems (and therefore relinquishes (1) ) . However, this view blasts the framework of the "orthodox quantum theory."
One more remark to Margenau's Sec. 7. In the characterisation of quantum mechanics the brief little sentence will be found: "on the classical level it corresponds to ordinary dynamics." This is entirely correct - cum grano salis; and it is precisely this granum salis which is significant for the question of interpretation.
If our concern is with macroscopic masses (billiard balls or stars), we are operating with very short de Broglie-waves, which are determinative for the behaviour of the center of gravity of such masses. This is the reason why it is possible to arrange the quantum-theoretical description for a reasonable time in such a manner that for the macroscopic way of viewing things, it becomes sufficiently precise in position as well as in momentum. It is true also that this sharpness remains for a long time and that the quasi-points thus represented behave just like the mass-points of classical mechanics. However, the theory shows also that, after a sufficiently long time, the point-like character of the Psi-function is completely lost to the center of gravity-co-ordinates, so that one can no longer speak of any quasi-localisation of the centers of gravity. The picture then becomes, for example in the case of a single macro-mass-point, quite similar to that involved in a single free electron.
If now, in accordance with the orthodox position, I view the Psi-function as the complete description of a real matter of fact for the individual case, I cannot but consider the essentially unlimited lack of sharpness of the position of the (macroscopic) body as real. On the other hand, however, we know that, by illuminating the body by means of a lantern at rest against the system of co-ordinates, we get a (macroscopically judged) sharp determination of position. In order to comprehend this I must assume that that sharply defined position is determined not merely by the real situation of the observed body, but also by the act of illumination. This is again a paradox (similar to the mark on the paper strip in the above mentioned example). The spook disappears only if one relinquishes the orthodox standpoint, according to which the Psi-function is accepted as a complete description of the single system.
It may appear as if all such considerations were just superfluous learned hairsplitting, which have nothing to do with physics proper. However, it depends precisely upon such considerations in which direction one believes one must look for the future conceptual basis of physics.
I close these expositions, which have grown rather lengthy, concerning the interpretation of quantum theory with the reproduction of a brief conversation which I had with an important theoretical physicist. He: "I am inclined to believe in telepathy." I: "This has probably more to do with physics than with psychology." He: "Yes."
The essays by Lenzen and Northrop both aim to treat my occasional utterances of epistemological content systematically. From those utterances Lenzen constructs a synoptic total picture, in which what is missing in the utterances is carefully and with delicacy of feeling supplied. Everything said therein appears to me convincing and correct. Northrop uses these utterances as point of departure for a comparative critique of the major epistemological systems. I see in this critique a masterpiece of unbiased thinking and concise discussion, which nowhere permits itself to be diverted from the essential.
The reciprocal relationship of epistemology and science is of noteworthy kind. They are dependent upon each other. Epistemology without contact with science becomes an empty scheme. Science without epistemology is - insofar as it is thinkable at all - primitive and muddled. However, no sooner has the epistemologist, who is seeking a clear system, fought his way through to such a system, than he is inclined to interpret the thought-content of science in the sense of his system and to reject whatever does not fit into his system. The scientist, however, cannot afford to carry his striving for epistemological systematic that far. He accepts gratefully the epistemological conceptual analysis; but the external conditions, which are set for him by the facts of experience, do not permit him to let himself be too much restricted in the construction of his conceptual world by the adherence to an epistemological system. He therefore must appear to the systematic epistemologist as a type of unscrupulous opportunist: he appears as realist insofar as he seeks to describe a world independent of the acts of perception; as idealist insofar as he looks upon the concepts and theories as the free inventions of the human spirit (not logically derivable from what is empirically given); as positivist insofar as he considers his concepts and theories justified only to the extent to which they furnish a logical representation of relations among sensory experiences. He may even appear as Platonist or Pythagorean insofar as he considers the viewpoint of logical simplicity as an indispensable and effective tool of his research.
All of this is splendidly elucidated in Lenzen's and Northrop's essays.
And now a few remarks concerning the essays by E. A. Milne, G. Lemaitre, and L. Infeld as concerns the cosmological problem:
Concerning Milne's ingenious reflections I can only say that I find their theoretical basis too narrow. From my point of view one cannot arrive, by way of theory, at any at least somewhat reliable results in the field of cosmology, if one makes no use of the principle of general relativity.
As concerns Lemaître's arguments in favour of the so-called "cosmological constant" in the equations of gravitation, I must admit that these arguments do not appear to me as sufficiently convincing in view of the present state of our knowledge.
The introduction of such a constant implies a considerable renunciation of the logical simplicity of theory, a renunciation which appeared to me unavoidable only so long as one had no reason to doubt the essentially static nature of space. After Hubble's discovery of the "expansion" of the stellar system, and since Friedmann's discovery that the unsupplemented equations involve the possibility of the existence of an average (positive) density of matter in an expanding universe, the introduction of such a constant appears to me, from the theoretical standpoint, at present unjustified.
The situation becomes complicated by the fact that the entire duration of the expansion of space to the present, based on the equations in their simplest form, turns out smaller than appears credible in view of the reliably known age of terrestrial minerals. But the introduction of the "cosmological constant" offers absolutely no natural escape from the difficulty. This latter difficulty is given by way of the numerical value of Hubble's expansion-constant and the age-measurement of minerals, completely independent of any cosmological theory, provided that one interprets the Hubble-effect as Doppler effect.
Everything finally depends upon the question: Can a spectral line be considered as a measure of a "proper time" (Eigen-Zeit) ds (ds2 = gikdxidxk), (if one takes into consideration regions of cosmic dimensions)? Is there such a thing as a natural object which incorporates the "natural-measuring-stick" independently of its position in four-dimensional space? The affirmation of this question made the invention of the general theory of relativity psychologically possible; however this supposition is logically not necessary. For the construction of the present theory of relativity the following is essential:
(1) Physical things are described by continuous functions, field-variables of four co-ordinates. As long as the topological connection is preserved, these latter can be freely chosen.
(2) The field-variables are tensor-components; among the tensors is a symmetrical tensor gik for the description of the gravitational field.
(3) There are physical objects, which (in the macroscopic field) measure the invariant ds.
If (1) and (2) are accepted, (3) is plausible, but not necessary. The construction of mathematical theory rests exclusively upon (1) and (2).
A complete theory of physics as a totality, in accordance with (1) and (2) does not yet exist. If it did exist, there would be no room for the supposition (3). For the objects used as tools for measurement do not lead an independent existence alongside of the objects implicated by the field-equations. - - It is not necessary that one should permit one's cosmological considerations to be restrained by such a sceptical attitude; but neither should one close one's mind towards them from the very beginning.
These reflections bring me to Karl Menger's essay. For the quantum-facts suggest the suspicion that doubt may also be raised concerning the ultimate usefulness of the program characterised in (1) and (2). There exists the possibility of doubting only (2) and, in doing so, to question the possibility of being able adequately to formulate the laws by means of differential equations, without dropping (1). The more radical effort of surrendering (1) with (2) appears to me - and I believe to Dr. Menger also - to lie more closely at hand. So long as no one has new concepts, which appear to have sufficient constructive power, mere doubt remains; this is, unfortunately, my own situation. Adhering to the continuum originates with me not in a prejudice, but arises out of the fact that I have been unable to think up anything organic to take its place. How is one to conserve four-dimensionality in essence (or in near approximation) and [at the same time] surrender the continuum?
L. Infeld's essay is an independently understandable, excellent introduction into the so-called "cosmological problem" of the theory of relativity, which critically examines all essential points.
Max von Laue: An historical investigation of the development of the conservation postulates, which, in my opinion, is of lasting value. I think it would be worth while to make this essay easily accessible to students by way of independent publication.
In spite of serious efforts I have not succeeded in quite understanding H. Dingle's essay, not even as concerns its aim. Is the idea of the special theory of relativity to be expanded in the sense that new group-characteristics, which are not implied by the Lorentz-invariance, are to be postulated? Are these postulates empirically founded or only by way of a trial "posited"? Upon what does the confidence in the existence of such group-characteristics rest?
Kurt Gödel's essay constitutes, in my opinion, an important contribution to the general theory of relativity, especially to the analysis of the concept of time. The problem here involved disturbed me already at the time of the building up of the general theory of relativity, without my having succeeded in clarifying it. Entirely aside from the relation of the theory of relativity to idealistic philosophy or to any philosophical formulation of questions, the problem presents itself as follows:
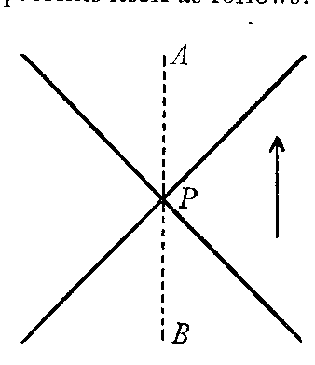
If P is a world-point, a "light-cone" (ds2= 0) belongs to it. We draw a "time-like" world-line through P and on this line observe the close world-points B and A, separated by P. Does it make any sense to provide the world-line with an arrow, and to assert that B is before P, A after P? Is what remains of temporal connection between world-points in the theory of relativity an asymmetrical relation, or would one be just as much justified, from the physical point of view, to indicate the arrow in the opposite direction and to assert that A is before P, B after P?
In the first instance the alternative is decided in the negative, if we are justified in saying: If it is possible to send (to telegraph) a signal (also passing by in the close proximity of P) from B to A, but not from A to B, then the one-sided (asymmetrical) character of time is secured, i.e., there exists no free choice for the direction of the arrow. What is essential in this is the fact that the sending of a signal is, in the sense of thermodynamics, an irreversible process, a process which is connected with the growth of entropy (whereas, according to our present knowledge, all elementary processes are reversible).
If, therefore, B and A are two, sufficiently neighbouring, world-points, which can be connected by a time-like line, then the assertion: "B is before A," makes physical sense. But does this assertion still make sense, if the points, which are connectable by the time-like line, are arbitrarily far separated from each other? Certainly not, if there exist point-series connectable by time-like lines in such a way that each point precedes temporally the preceding one, and if the series is closed in itself. In that case the distinction "earlier-later" is abandoned for world-points which lie far apart in a cosmological sense, and those paradoxes, regarding the direction of the causal connection, arise, of which Mr. Gödel has spoken.
Such cosmological solutions of the gravitation-equations (with not vanishing A-constant) have been found by Mr. Gödel. It will be interesting to weigh whether these are not to be excluded on physical grounds.
I have the distressing feeling that I have expressed myself, in this reply, not merely somewhat longwindedly but also rather sharply. This observation may serve as my excuse: one can really quarrel only with his brothers or close friends; others are too alien [for that].
P.S. The preceding remarks refer to essays which were in my hands at the end of January 1949. Inasmuch as the volume was to have appeared in March, it was high time to write down these reflections.
After they had been concluded I learned that the publication of the volume would experience a further delay and that some additional important essays had come in. I decided, nevertheless, not to expand my remarks further, which had already become too long, and to desist from taking any position with reference to those essays which came into my hands after the conclusion of my remarks.