[1]   Y. Aharonov and D. Bohm. Significance of electromagnetic potentials in quantum theory. Phys. Rev., 115(3):485, 1959.

[2]   V. Allori and N. Zanghi. On the classical limit of quantum mechanics. Foundations of Physics, 39:20–32, 2009.

[3]   P. W. Anderson. More is different. Science, 177(4047):393–396, August 1972.

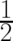[4]   V. Arunsalam. Hamiltonians and wave equations for particles of spin and spin with nonzero mass. Am. J. Phys., 38:1010–1022, 1970.

[5]   L. E. Ballentine. The statistical interpretation of quantum mechanics. Reviews of Modern Physics, 42:358–381, 1970.

[6]   L. E. Ballentine. Inadequacy of Ehrenfest’s theorem to characterize the classical regime. Physical Review, A 50:2854–2859, 1994.

[7]   F. J. Belinfante. Can individual elementary particles have individual properties? Am. J. Phys., 46(4):329–336, 1978.

[8]   Y. F. Bow. The hamiltonian of a charged particle in a rotating frame. Am. J. Phys, 40:252–256, 1972.

[9]   V. Colussi and S. Wickramasekara. Galilean and U(1)-gauge symmetry of the Schrödinger field. Annals of Physics, 323:3020–3036, 2008.

[10]   C. A. Dartora and G. G. Cabrera. Magnetization, spin current, and spin-transfer torque from SU(2) local gauge invariance of the nonrelativistic Pauli-Schrödinger theory. Physical Review, B 78:012403, 2008.

[11]   B. Roy Frieden. Science from Fisher Information, a Unification. Cambridge University Press, Cambridge, 2004.

[12]   R. J. Gould. The intrinsic magnetic moment of elementary particles. Am. J. Phys., 64:597–601, 1995.

[13]   W. Greiner. Classical Mechanics, Systems of particles and Hamiltonian dynamics. Springer, New York, 1989.

[14]   P. R. Holland. The quantum theory of motion. Cambridge University Press, Cambridge, U.K., 1995.

[15]   R. J. Hughes. On Feynman’s proof of the Maxwell equations. Am. J. Phys., 60:301–306, 1992.

[16]   John David Jackson. Classical Electrodynamics. John Wiley & Sons, 3rd edition, 1998.

[17]   F. A. Kaempfer. Concepts in Quantum Mechanics. Academic Press, New York, 1965.

[18]   U. Klein. The statistical origins of quantum mechanics. arxiv:0810.2394.

[19]   U. Klein. Schrödinger’s equation with gauge coupling derived from a continuity equation. Foundations of physics, 39:964, 2009. arxiv:0806.4335.

[20]   D. H. Kobe and K. Yang. Gauge transformation of the time-evolution operator. Phys. Rev. A, 32:952–958, 1985.

[21]   L. D. Landau and E. M. Lifshitz. Classical theory of fields, volume II of Course of theoretical physics. Pergamon Press, Oxford, 2 edition, 1962.

[22]   L. J. Landau. Macroscopic observation of a quantum particle in a slowly varying potential - on the classical limit of quantum theory. Annals of Physics, 246:190–227, 1996.

[23]   R. B. Laughlin and D. Pines. The theory of everything. Proc. Natl. Acad. Sci. USA, 97:28–31, 2000.

[24]   H. Margenau. Measurements in quantum mechanics. Annals of Physics, 23:469–485, 1963.

[25]   B. Mashhoon and H. Kaiser. Inertia of intrinsic spin. Physica B, 385-386:1381–1383, 2006.

[26]   M. Morrison. Spin: All is not what it seems. Studies in history and philosophy of modern physics, 38:529–557, 2007.

[27]   M. Peshkin and A. Tonomura. The Aharonov-Bohm Effect. Lecture Notes in Physics. Springer Verlag, Berlin, 1989.

[28]   M. Reginatto. Derivation of the Pauli equation using the principle of minimum Fisher information. Physics Letters, A 249:355–357, 1998.

[29]   E. G. P. Rowe. Classical limit of quantum mechanics (electron in a magnetic field). Am. J. Phys., 59:1111–1117, 1991.

[30]   R. Schiller. Quasi-classical theory of the nonspinning electron. Phys. Rev., 125(3):1100–1108, February 1962.

[31]   R. Schiller. Quasi-Classical Theory of the Spinning Electron. Phys. Rev., 125(3):1116–1123, February 1962.

[32]   H. Shirai. Reinterpretation of quantum mechanics based on the statistical interpretation. Foundations of Physics, 28:1633–1662, 1998.

[33]   J. J. Slawianowski. Quantum relations remaining valid on the classical limit. Rep. Math. Phys., 2:11–34, 1970.

[34]   T. Takabayasi. The vector representation of spinning particles in the quantum theory I. Progress in Theoretical Physics., 14:283–302, 1955.

[35]   J. H. Van Vleck. The correspondence principle in the statistical interpretation of quantum mechanics. Proc. Natl. Acad. Sci. U.S., 14:178–188, 1928.

[36]   R. F. Werner and M. P. H. Wolff. Classical mechanics as quantum mechanics with infinitesimal . Physics Letters A, 202:155–159, 1995.