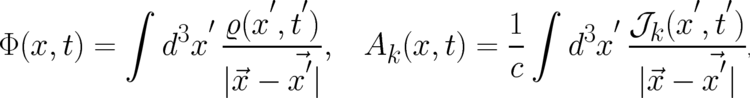
A possible set of additional assumptions selecting Maxwell’s theory from the class of all possible gauge fields is given by
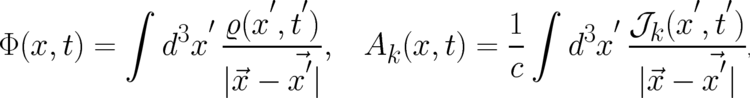 | (110) |
Here, the potentials are written in terms of four localized functions 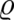 and
and 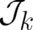 , where
, where
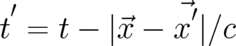 and
and 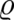 and
and 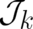 obey a continuity equation. The quantities (110) are
well known as retarded potentials in Lorentz gauge [16]. Using the representation (110) it may easily be shown
that the corresponding fields
obey a continuity equation. The quantities (110) are
well known as retarded potentials in Lorentz gauge [16]. Using the representation (110) it may easily be shown
that the corresponding fields 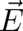 and
and 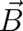 obey the full set of Maxwell’s equations, including the two
inhomogeneous equations with sources
obey the full set of Maxwell’s equations, including the two
inhomogeneous equations with sources 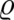 and
and 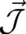 ,
,
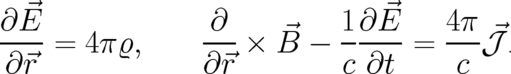 | (111) |
An alternative possibility is, of course, to postulate the validity of Eqs. (111) for the fields directly, without making use of potentials. The interesting problem of the coexistence of the Galilei-invariant Schrödinger equation and the Lorentz-invariant Maxwell equations has been discussed recently [9].
It is less well-known that inertial forces and linearized gravitational forces provide an alternative realization,
besides electrodynamics, for the fields 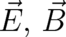 [15]. We restrict ourselves here to a discussion of inertial
forces, whose description in a quantum-theoretical context seems particularly interesting. Let us consider a
particle in an arbitrary accelerated reference frame, whose movement relative to an inertial frame is given by a
translation vector
[15]. We restrict ourselves here to a discussion of inertial
forces, whose description in a quantum-theoretical context seems particularly interesting. Let us consider a
particle in an arbitrary accelerated reference frame, whose movement relative to an inertial frame is given by a
translation vector 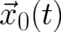 and a rotation velocity
and a rotation velocity 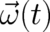 . As is well known such a particle experiences an
inertial force field
. As is well known such a particle experiences an
inertial force field
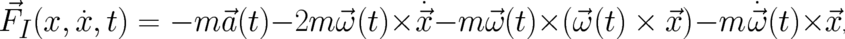 | (112) |
where 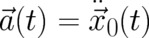 . In order to use Eq. (112) in the present field theory, the particle velocity
. In order to use Eq. (112) in the present field theory, the particle velocity
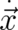 has to be replaced by the velocity field (34) and the electric charge
has to be replaced by the velocity field (34) and the electric charge 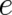 by the ’gravitational
charge’
by the ’gravitational
charge’ 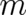 . Then, comparison of Eqs. (112) and (35) shows that inertial forces are described by a
field
. Then, comparison of Eqs. (112) and (35) shows that inertial forces are described by a
field
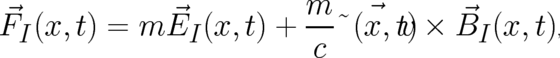 | (113) |
where
![B⃗I (x, t ) = 2 c ⃗ω (t)
E⃗ (x, t) = - ⃗a (t ) - ⃗ω (t ) × [⃗ω (t ) × ⃗x ] - ⃗ω˙ (t) × ⃗x.
I](soq3dweb524x.png) | (114) (115) |
![1- 2
φI (x, t ) = ⃗x ⃗a (t ) - [⃗x × ⃗ω (t )]
2
A⃗ (x, t) = c ⃗ω (t) × ⃗x.
I](soq3dweb525x.png) | (116) (117) |
We see that inertial forces do also fit into the above gauge scheme although fundamental differences exist. In
contrast to the electrodynamic field there are no additional field equations for the inertial field. Rather, its
space-time dependence is more or less ’rigid’ and can only be influenced by means of the input parameters
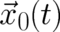 and
and 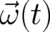 . Inertial fields do in contrast to electrodynamical fields not fit into the mathematical
scheme gauge theory.
. Inertial fields do in contrast to electrodynamical fields not fit into the mathematical
scheme gauge theory.
The fact that electrodynamical and inertial (gravitational) fields share a common (gauge) constraint, is
sometimes interpreted as an indication of a common origin of both theories. We do not want to discuss this
fascinating hypothesis here but mention only that these two gauge fields may also occur simultaneously; such a
situation may simply be described by means of a linear combination of fields and potentials. Of course, the
electrodynamic fields 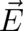 and
and 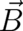 are now defined with respect to the accelerated coordinate frame.
(The homogeneous Maxwell equations hold in the accelerated frame as well; this is a condition
for the potentials to exist. On the other hand the two inhomogeneous Maxwell equations change
their form in accelerated coordinate frames [8]). In order to obtain Schrödinger’s equation for a
statistical ensemble of charged particles in arbitrary accelerated reference frames, the replacements
are now defined with respect to the accelerated coordinate frame.
(The homogeneous Maxwell equations hold in the accelerated frame as well; this is a condition
for the potentials to exist. On the other hand the two inhomogeneous Maxwell equations change
their form in accelerated coordinate frames [8]). In order to obtain Schrödinger’s equation for a
statistical ensemble of charged particles in arbitrary accelerated reference frames, the replacements
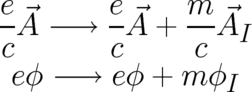 | (118) (119) |
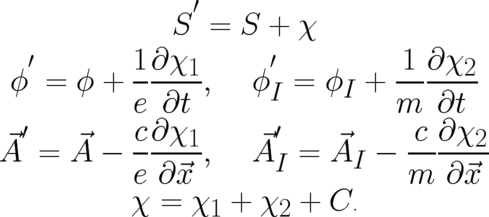 | (120) (121) (122) (123) |