3 Statistical conditions
In this section we combine and rewrite the statistical conditions in order to obtain a single relation that will be
useful in later sections .
We begin with the first statistical condition (6). The following calculation is very similar to the
corresponding one-dimensional calculation reported in I; thus details may be omitted. We insert the
definition (8) in (6) and replace the derivative of 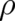 with respect to
with respect to 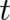 by the second term in the continuity
equation (5). Using Gauss’ integral theorem and assuming that
by the second term in the continuity
equation (5). Using Gauss’ integral theorem and assuming that 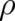 vanishes sufficiently rapidly for
vanishes sufficiently rapidly for
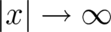 in order for the surface integral to vanish (we may even assume that it vanishes faster than
an arbitrary finite power of
in order for the surface integral to vanish (we may even assume that it vanishes faster than
an arbitrary finite power of 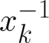 ) we arrive at the following expression for the expectation value of the
momentum
) we arrive at the following expression for the expectation value of the
momentum
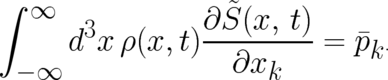 | (13) |
This relation agrees essentially with the corresponding one-dimensional relation obtained in I.
We study now the implications of the second statistical condition (7). We start by evaluating the left hand
side of (7). Using the variables 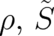 it is given by
it is given by
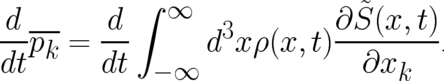 | (14) |
Performing the derivative with respect to 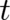 Eq. (14) takes the form
Eq. (14) takes the form
![[ ]
∫ ∞
d ---- 3 ∂ ρ (x, t) ∂ S˜ (x, t ) ∂ ∂ ˜S (x, t)
----p = d x -------------------------- + ρ (x, t )----------------- .
dt k ∂ t ∂ x ∂ t ∂ x
- ∞ k k](soq3dweb84x.png) | (15) |
Note that each term in the integrand of (15) is single-valued but 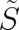 is not. As a consequence the order of two
derivatives of
is not. As a consequence the order of two
derivatives of 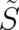 (with respect to anyone of the variables
(with respect to anyone of the variables 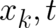 ) must not be changed. We introduce the
(single-valued) quantities
) must not be changed. We introduce the
(single-valued) quantities
![[ ] [ ]
2 ˜ 2 ˜ 2 ˜ 2 ˜
˜ ---∂---S----- ---∂---S----- ˜ -∂---S---- --∂---S---
S [j,k ] = - , S [0,k ] = -
∂ xj ∂ xk ∂ xk ∂ xj ∂ t∂ xk ∂ xk ∂ t](soq3dweb88x.png) | (16) |
to describe the non-commuting derivatives.
Evaluating the first term in the integrand of (15) we replace the time derivative of 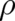 by the divergence of
the probability current according to the continuity equation (5) to obtain
by the divergence of
the probability current according to the continuity equation (5) to obtain
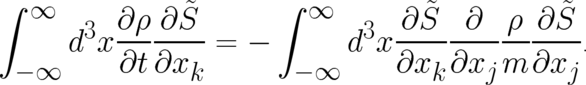 | (17) |
Performing a partial integration and exchanging the derivatives with respect to 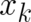 and
and 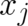 , Eq. (17)
takes the form
, Eq. (17)
takes the form
![[ ]
∫ ∞ ˜ ∫ ∞ ˜ ˜
3 ∂ ρ ∂ S 3 ρ ∂ S ∂ ∂ S
d x ----------- = d x ----------- --------------+ S˜[j,k ] .
∂ t ∂ x m ∂ x ∂ x ∂ x
- ∞ k - ∞ j k j](soq3dweb93x.png) | (18) |
Using the formula
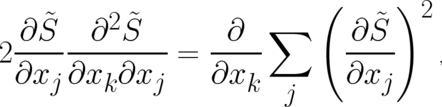 | (19) |
and performing a second partial integration the first term in the integrand of (15) takes the form
![∫
∞ ∂ ρ ∂ S˜
d3x ------------ =
- ∞ ∂ t ∂ xk
∫ ( )2 ∫ ,
∞ ∑ ˜ ∞ ˜
3 -∂--ρ----1--- -∂-S--- 3 --ρ----∂-S---˜
- d x + d x S [j,k ]
- ∞ ∂ xk 2m ∂ xj - ∞ 2m ∂ xj
j](soq3dweb95x.png) | (20) |
Similar manipulations lead to the following expression for the second term in the integrand of (15):
![∫ ∫ ∫
∞ ∂ ∂ ˜S ∞ ∂ ρ ∂ S˜ ∞
3 ----------- 3 ------------ 3 ˜
d x ρ = - d x + d x ρ S [0,k ],
- ∞ ∂ t ∂ xk - ∞ ∂ xk ∂ t - ∞](soq3dweb96x.png) | (21) |
Let us assume that the the macroscopic force 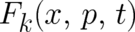 entering the second statistical
condition (7) can be written as a sum of two contributions,
entering the second statistical
condition (7) can be written as a sum of two contributions, 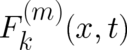 and
and 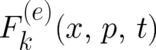 ,
,
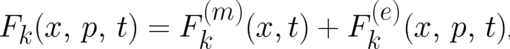 | (22) |
where 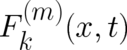 takes the form of a negative gradient of a scalar function
takes the form of a negative gradient of a scalar function 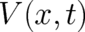 (mechanical potential). Since
(mechanical potential). Since 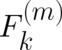 does (in contrast to
does (in contrast to 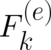 ) not depend on
) not depend on 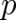 , its average value
can be calculated with the help of a known probability distribution, namely the dynamical variable
, its average value
can be calculated with the help of a known probability distribution, namely the dynamical variable 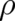 .
Performing a partial integration and collecting terms the second statistical condition (7) takes the
form.
.
Performing a partial integration and collecting terms the second statistical condition (7) takes the
form.
![⌊ ( ) ⌋
∫ ∞ 2
3 ∂ ρ ∂ ˜S 1 ∑ ∂ S˜
- d x ------- ⌈ ----- + ------ ------- + V ⌉
∂ x ∂ t 2m ∂ x
- ∞ k j j
[ ] ,
∫ ∞ ---------------------
1 ∂ S˜ (e )
+ d3x ρ ----------S˜ + S˜ = F (x, p, t )
m ∂ x [j,k ] [0,k ] k
- ∞ j](soq3dweb107x.png) | (23) |
Comparing Eq. (23) with the corresponding formula obtained in I [see Eq. (24) of I] we see that two new terms
appear now, namely the expectation value of the 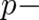 dependent force on the r.h.s. and the second term on
the l.h.s. of Eq. (23). The latter is a direct consequence of our assumption of a multi-valued variable
dependent force on the r.h.s. and the second term on
the l.h.s. of Eq. (23). The latter is a direct consequence of our assumption of a multi-valued variable
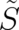 .
.
In the next section it will be shown that for vanishing multi-valuedness Eq. (23) has to agree with the
three-dimensional generalization of the corresponding result [Eq. (24) of I] obtained in I. This means that the
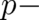 dependent term on the r.h.s. has to vanish too in this limit and indicates a relation between
multi-valuedness of
dependent term on the r.h.s. has to vanish too in this limit and indicates a relation between
multi-valuedness of 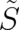 and
and 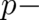 dependence of the external force.
dependence of the external force.
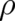 with respect to
with respect to 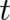 by the second term in the continuity
equation (5). Using Gauss’ integral theorem and assuming that
by the second term in the continuity
equation (5). Using Gauss’ integral theorem and assuming that 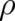 vanishes sufficiently rapidly for
vanishes sufficiently rapidly for
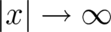 in order for the surface integral to vanish (we may even assume that it vanishes faster than
an arbitrary finite power of
in order for the surface integral to vanish (we may even assume that it vanishes faster than
an arbitrary finite power of 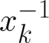 ) we arrive at the following expression for the expectation value of the
momentum
) we arrive at the following expression for the expectation value of the
momentum
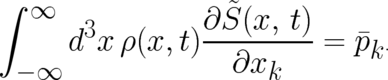
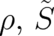 it is given by
it is given by
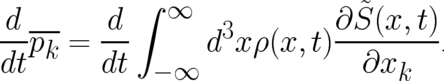
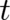 Eq. (
Eq. (![[ ]
∫ ∞
d ---- 3 ∂ ρ (x, t) ∂ S˜ (x, t ) ∂ ∂ ˜S (x, t)
----p = d x -------------------------- + ρ (x, t )----------------- .
dt k ∂ t ∂ x ∂ t ∂ x
- ∞ k k](soq3dweb84x.png)
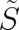 is not. As a consequence the order of two
derivatives of
is not. As a consequence the order of two
derivatives of 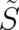 (with respect to anyone of the variables
(with respect to anyone of the variables 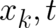 ) must not be changed. We introduce the
(single-valued) quantities
) must not be changed. We introduce the
(single-valued) quantities
![[ ] [ ]
2 ˜ 2 ˜ 2 ˜ 2 ˜
˜ ---∂---S----- ---∂---S----- ˜ -∂---S---- --∂---S---
S [j,k ] = - , S [0,k ] = -
∂ xj ∂ xk ∂ xk ∂ xj ∂ t∂ xk ∂ xk ∂ t](soq3dweb88x.png)
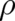 by the divergence of
the probability current according to the continuity equation (
by the divergence of
the probability current according to the continuity equation (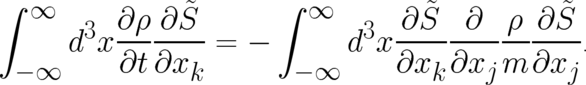
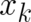 and
and 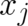 , Eq. (
, Eq. (![[ ]
∫ ∞ ˜ ∫ ∞ ˜ ˜
3 ∂ ρ ∂ S 3 ρ ∂ S ∂ ∂ S
d x ----------- = d x ----------- --------------+ S˜[j,k ] .
∂ t ∂ x m ∂ x ∂ x ∂ x
- ∞ k - ∞ j k j](soq3dweb93x.png)
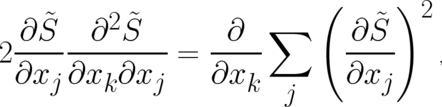
![∫
∞ ∂ ρ ∂ S˜
d3x ------------ =
- ∞ ∂ t ∂ xk
∫ ( )2 ∫ ,
∞ ∑ ˜ ∞ ˜
3 -∂--ρ----1--- -∂-S--- 3 --ρ----∂-S---˜
- d x + d x S [j,k ]
- ∞ ∂ xk 2m ∂ xj - ∞ 2m ∂ xj
j](soq3dweb95x.png)
![∫ ∫ ∫
∞ ∂ ∂ ˜S ∞ ∂ ρ ∂ S˜ ∞
3 ----------- 3 ------------ 3 ˜
d x ρ = - d x + d x ρ S [0,k ],
- ∞ ∂ t ∂ xk - ∞ ∂ xk ∂ t - ∞](soq3dweb96x.png)
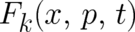 entering the second statistical
condition (
entering the second statistical
condition (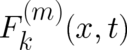 and
and 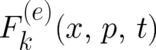 ,
,
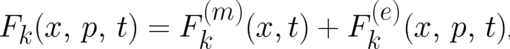
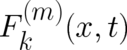 takes the form of a negative gradient of a scalar function
takes the form of a negative gradient of a scalar function 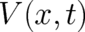 (mechanical potential). Since
(mechanical potential). Since 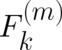 does (in contrast to
does (in contrast to 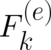 ) not depend on
) not depend on 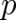 , its average value
can be calculated with the help of a known probability distribution, namely the dynamical variable
, its average value
can be calculated with the help of a known probability distribution, namely the dynamical variable 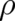 .
Performing a partial integration and collecting terms the second statistical condition (
.
Performing a partial integration and collecting terms the second statistical condition (![⌊ ( ) ⌋
∫ ∞ 2
3 ∂ ρ ∂ ˜S 1 ∑ ∂ S˜
- d x ------- ⌈ ----- + ------ ------- + V ⌉
∂ x ∂ t 2m ∂ x
- ∞ k j j
[ ] ,
∫ ∞ ---------------------
1 ∂ S˜ (e )
+ d3x ρ ----------S˜ + S˜ = F (x, p, t )
m ∂ x [j,k ] [0,k ] k
- ∞ j](soq3dweb107x.png)
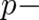 dependent force on the r.h.s. and the second term on
the l.h.s. of Eq. (
dependent force on the r.h.s. and the second term on
the l.h.s. of Eq. (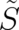 .
.
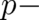 dependent term on the r.h.s. has to vanish too in this limit and indicates a relation between
multi-valuedness of
dependent term on the r.h.s. has to vanish too in this limit and indicates a relation between
multi-valuedness of 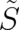 and
and 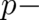 dependence of the external force.
dependence of the external force.