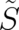 ,
, 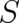 , and
, and
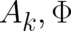 introduced at the beginning of section 2. The multi-valued function
introduced at the beginning of section 2. The multi-valued function 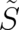 may be
represented [17],[19] in the form
may be
represented [17],[19] in the form
At this stage of our study it may be useful to clarify the physical role of the quantities 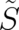 ,
, 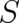 , and
, and
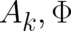 introduced at the beginning of section 2. The multi-valued function
introduced at the beginning of section 2. The multi-valued function 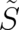 may be
represented [17],[19] in the form
may be
represented [17],[19] in the form
![∫
x,t [ ]
˜ e- ′ ′ ′ ′ ′ ′
S (x, t; C ) = S (x, t )- dx kAk (x , t ) - cdt φ (x , t ) ,
c x ,t ;C
0 0](soq3dweb117x.png) | (24) |
as a path-integral performed along an arbitrary path 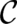 in four-dimensional space; the multi-valuedness of
in four-dimensional space; the multi-valuedness of
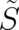 means simply that it depends not only on
means simply that it depends not only on 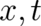 but also on the path
but also on the path 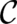 connecting the points
connecting the points
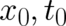 and
and 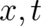 .
.
The quantity 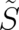 cannot be a physical observable because of its multi-valuedness. The fundamental physical
quantities to be determined by our (future) theory are the four derivatives of
cannot be a physical observable because of its multi-valuedness. The fundamental physical
quantities to be determined by our (future) theory are the four derivatives of 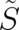 [see (3)] which will be
rewritten here using the above notation
[see (3)] which will be
rewritten here using the above notation
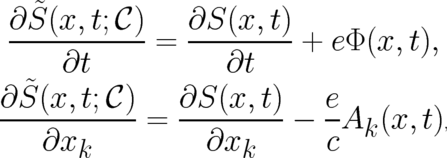 | (25) (26) |
 . We have to use instead the
decompositions as given by the right hand sides of (25) and (26). The latter terms are single-valued (in the
sense of the above definition) but need not be unique because only the left hand sides are uniquely determined
by the physical situation. We tentatively assume that the fields
. We have to use instead the
decompositions as given by the right hand sides of (25) and (26). The latter terms are single-valued (in the
sense of the above definition) but need not be unique because only the left hand sides are uniquely determined
by the physical situation. We tentatively assume that the fields  and
and  are ’given’ quantities in the
sense that they represent an external influence (of ’external forces’) on the considered statistical situation. An
actual calculation has to be performed in such a way that fixed fields
are ’given’ quantities in the
sense that they represent an external influence (of ’external forces’) on the considered statistical situation. An
actual calculation has to be performed in such a way that fixed fields 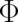 and
and 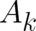 are chosen and then the
differential equations are solved for
are chosen and then the
differential equations are solved for 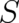 (and
(and 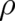 ). However, as mentioned already, what is actually
uniquely determined by the physical situation is the sum of the two terms on the right hand sides
of (25) (26). Consequently, a different set of fixed fields
). However, as mentioned already, what is actually
uniquely determined by the physical situation is the sum of the two terms on the right hand sides
of (25) (26). Consequently, a different set of fixed fields 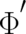 and
and 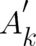 may lead to a different solution
may lead to a different solution
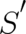 in such a way that the sum of the new terms [on the right hand sides of (25) and (26)] is the
same as the sum of the old terms. We assume here, that the formalism restores the values of the
physically relevant terms. This implies that the relation between the old and new terms is given by
in such a way that the sum of the new terms [on the right hand sides of (25) and (26)] is the
same as the sum of the old terms. We assume here, that the formalism restores the values of the
physically relevant terms. This implies that the relation between the old and new terms is given by
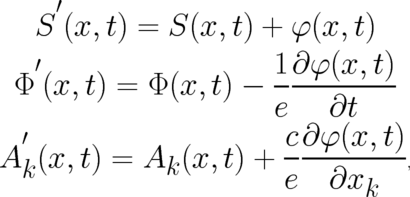 | (27) (28) (29) |
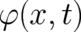 is an arbitrary, single-valued function of
is an arbitrary, single-valued function of 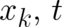 . Consequently, all
’theories’ (differential equations for
. Consequently, all
’theories’ (differential equations for 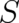 and
and 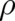 defined by the assumptions listed in section 2) will be
form-invariant under the transformations (27)-(29). These invariance transformations are (using an arbitrary
function
defined by the assumptions listed in section 2) will be
form-invariant under the transformations (27)-(29). These invariance transformations are (using an arbitrary
function 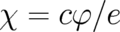 instead of
instead of 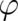 ) denoted as ’gauge transformations of the second
kind’.
) denoted as ’gauge transformations of the second
kind’.
The fields 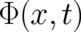 and
and 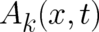 describe an external influence but their numerical value is
undefined; their value at
describe an external influence but their numerical value is
undefined; their value at 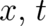 may be changed according to (28) and (29) without changing their physical
effect. Thus, these fields cannot play a local role in space and time like forces and fields in classical mechanics
and electrodynamics. What, then, is the physical meaning of these fields ? An explanation which seems obvious
in the present context is the following: They describe the statistical effect of an external influence on the
considered system (ensemble of identically prepared individual particles). The statistical effect of a force field on
an ensemble may obviously differ from the local effect of the same force field on individual particles;
thus the very existence of fields
may be changed according to (28) and (29) without changing their physical
effect. Thus, these fields cannot play a local role in space and time like forces and fields in classical mechanics
and electrodynamics. What, then, is the physical meaning of these fields ? An explanation which seems obvious
in the present context is the following: They describe the statistical effect of an external influence on the
considered system (ensemble of identically prepared individual particles). The statistical effect of a force field on
an ensemble may obviously differ from the local effect of the same force field on individual particles;
thus the very existence of fields 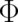 and
and 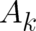 different from
different from 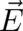 and
and 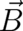 is no surprise.
The second common problem with the interpretation of the potentials
is no surprise.
The second common problem with the interpretation of the potentials 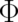 and
and 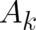 is their
non-uniqueness. It is hard to understand that a quantity ruling the behavior of individual particles
should not be uniquely defined. In contrast, this non-uniqueness is much easier to accept if
is their
non-uniqueness. It is hard to understand that a quantity ruling the behavior of individual particles
should not be uniquely defined. In contrast, this non-uniqueness is much easier to accept if 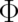 and
and
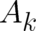 rule the behavior of ensembles instead of individual particles. We have no problem to accept
the fact that a function that represents a global (integral) effect may have many different local
realizations.
rule the behavior of ensembles instead of individual particles. We have no problem to accept
the fact that a function that represents a global (integral) effect may have many different local
realizations.
It seems that this interpretation of the ’potentials’ 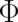 and
and 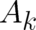 is highly relevant for the interpretation
of the Aharonov-Bohm effect [1], [27]. A statistical interpretation of the potentials has apparently never been
suggested, neither in the vast literature on the Aharonov-Bohm effect nor in papers promoting the statistical
interpretation of quantum mechanics; most physicists discuss this nonlocal ’paradox’ from the point of view of
”the wave function of a single electron”. Further discussion on the significance of the potentials may be found in
section 9.
is highly relevant for the interpretation
of the Aharonov-Bohm effect [1], [27]. A statistical interpretation of the potentials has apparently never been
suggested, neither in the vast literature on the Aharonov-Bohm effect nor in papers promoting the statistical
interpretation of quantum mechanics; most physicists discuss this nonlocal ’paradox’ from the point of view of
”the wave function of a single electron”. Further discussion on the significance of the potentials may be found in
section 9.
The expectation value 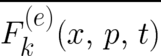 on the right hand side of (23) is to be calculated using
local, macroscopic forces (whose functional form is still unknown). Both the potentials and these local forces
represent an external influence, and it is plausible to assume that they are not independent from each other.
Thus it is reasonable to assume that the (nonlocal) potentials are statistical representations of
the same external (local) forces, occurring on the r.h.s. of Eq. (23). These local forces have to be
determined by the potentials but must be uniquely defined at each space-time point. The gauge-invariant
fields
on the right hand side of (23) is to be calculated using
local, macroscopic forces (whose functional form is still unknown). Both the potentials and these local forces
represent an external influence, and it is plausible to assume that they are not independent from each other.
Thus it is reasonable to assume that the (nonlocal) potentials are statistical representations of
the same external (local) forces, occurring on the r.h.s. of Eq. (23). These local forces have to be
determined by the potentials but must be uniquely defined at each space-time point. The gauge-invariant
fields
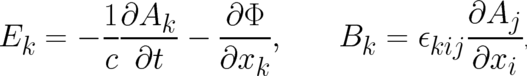 | (30) |
fulfill these requirements. As a consequence of the defining relations (30) they obey automatically the homogeneous Maxwell equations.
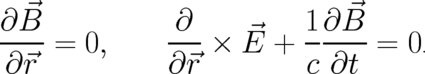 | (31) |
Note that from the present statistical (nonlocal) point of view the potentials are more fundamental than the local fields. In contrast, considered from the point of view of macroscopic physics, the local fields are the physical quantities of primary importance and the potentials may (or may not) be introduced for mathematical convenience.
As a next step we rewrite the second term on the l.h.s. of Eq. (23). The commutator terms (16) take the form
![( ) ( )
1 ∂ Ak ∂ Φ e ∂ Aj ∂ Ak
S˜ = - e ----------+ ------- , S˜ = -- ------- - -------- .
[0,k ] c ∂ t ∂ x [j,k ] c ∂ x ∂ x
k k j](soq3dweb160x.png) | (32) |
As a consequence, they may be expressed in terms of the local fields (30), which have been introduced above for reasons of gauge-invariance. Using (32),(30) and the relation (4) for the momentum field, Eq. (23) takes the form
![⌊ ( ) ⌋
∫ ∞ 2
∂ ρ ∂ S˜ 1 ∑ ∂ ˜S
- d3x -------⌈ ----- + ------ ------- + V ⌉
∂ x ∂ t 2m ∂ x
- ∞ k j j ,
∫ ---------------------
∞ [ e ]
3 -- (e )
+ d x ρ εkij ˜viBj + eEk = F k (x, p, t)
- ∞ c](soq3dweb161x.png) | (33) |
with a velocity field 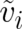 defined by
defined by
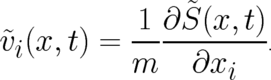 | (34) |
Thus, the new terms on the l.h.s. of (33) - stemming from the multi-valuedness of 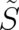 - take the form of an
expectation value (with
- take the form of an
expectation value (with 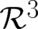 as sample space) of the Lorentz force field
as sample space) of the Lorentz force field
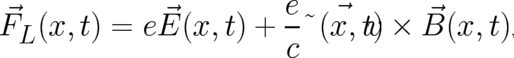 | (35) |
if the particle velocity is identified with the velocity field (34).
Let us discuss now the nature of the macroscopic forces 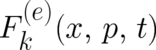 entering the expectation
value on the r.h.s. of Eq. (33). In our type I parent theory, classical mechanics, there are no constraints for the
possible functional form of
entering the expectation
value on the r.h.s. of Eq. (33). In our type I parent theory, classical mechanics, there are no constraints for the
possible functional form of 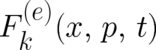 . However, this need not be true in the present statistical
framework. As a matter of fact, the way the mechanical potential
. However, this need not be true in the present statistical
framework. As a matter of fact, the way the mechanical potential 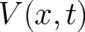 entered the differential
equation for
entered the differential
equation for  (in the previous work I) indicates already that such constraints do actually exist. Let us recall
that we tacitly restricted the class of forces to those derivable from a potential
(in the previous work I) indicates already that such constraints do actually exist. Let us recall
that we tacitly restricted the class of forces to those derivable from a potential 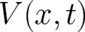 . If we eliminate
this restriction and admit arbitrary forces, with components
. If we eliminate
this restriction and admit arbitrary forces, with components 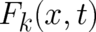 , we obtain instead of the above
relation (33) the simpler relation [Eq. (24) of I, generalized to three dimensions and arbitrary forces of the form
, we obtain instead of the above
relation (33) the simpler relation [Eq. (24) of I, generalized to three dimensions and arbitrary forces of the form
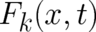 ]
]
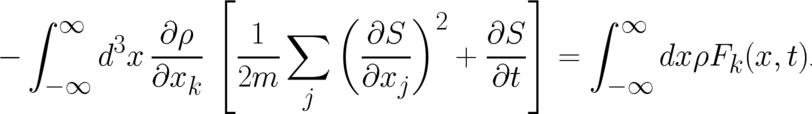 | (36) |
This is a rather complicated integro-differential equation for our variables 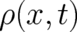 and
and 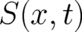 . We
assume now, using mathematical simplicity as a guideline, that Eq. (36) can be written in the common form of a
local differential equation. This assumption is of course not evident; in principle the laws of physics could be
integro-differential equations or delay differential equations or take an even more complicated mathematical
form. Nevertheless, this assumption seems rather weak considering the fact that all fundamental laws of
physics take this ’simple’ form. Thus, we postulate that Eq. (36) is equivalent to a differential
equation
. We
assume now, using mathematical simplicity as a guideline, that Eq. (36) can be written in the common form of a
local differential equation. This assumption is of course not evident; in principle the laws of physics could be
integro-differential equations or delay differential equations or take an even more complicated mathematical
form. Nevertheless, this assumption seems rather weak considering the fact that all fundamental laws of
physics take this ’simple’ form. Thus, we postulate that Eq. (36) is equivalent to a differential
equation
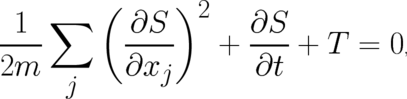 | (37) |
where the unknown term 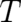 describes the influence of the force
describes the influence of the force 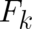 but may also contain other
contributions. Let us write
but may also contain other
contributions. Let us write
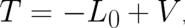 | (38) |
where 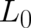 does not depend on
does not depend on 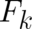 , while
, while 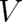 depends on it and vanishes for
depends on it and vanishes for  .
Inserting (37) and (38) in (36) yields
.
Inserting (37) and (38) in (36) yields
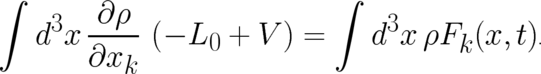 | (39) |
For  Eq. (39) leads to the relation
Eq. (39) leads to the relation
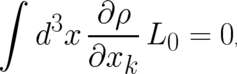 | (40) |
which remains true for finite forces because  does not depend on
does not depend on  . Finally, performing a partial
integration, we see that a relation
. Finally, performing a partial
integration, we see that a relation
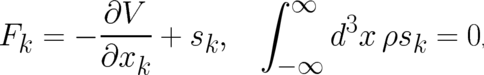 | (41) |
exists between 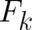 and
and 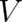 , with a vanishing expectation value of the (statistically irrelevant) functions
, with a vanishing expectation value of the (statistically irrelevant) functions
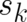 . This example shows that the restriction to gradient fields, made above and in I, is actually not necessary.
We may admit force fields which are arbitrary functions of
. This example shows that the restriction to gradient fields, made above and in I, is actually not necessary.
We may admit force fields which are arbitrary functions of 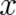 and
and 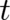 ; the statistical conditions (which play
now the role of a ’statistical constraint’) eliminate automatically all forces that cannot be written after statistical
averaging as gradient fields.
; the statistical conditions (which play
now the role of a ’statistical constraint’) eliminate automatically all forces that cannot be written after statistical
averaging as gradient fields.
This is very interesting and indicates the possibility that the present statistical assumptions leading to Schrödinger’s equation may also be responsible, at least partly, for the structure of the real existing (gauge) interactions of nature.
This statistical constraint may also work in the present 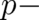 dependent case. We assume that the force
in (33) is a standard random variable with the configuration space as sample space (see the discussion in
section 4 of I) and that the variable
dependent case. We assume that the force
in (33) is a standard random variable with the configuration space as sample space (see the discussion in
section 4 of I) and that the variable 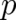 in
in 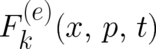 may consequently be replaced
by the field
may consequently be replaced
by the field 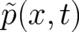 [see (4)]. Then, the expectation value on the r.h.s. of (33) takes the
form
[see (4)]. Then, the expectation value on the r.h.s. of (33) takes the
form
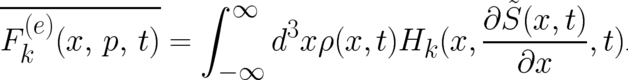 | (42) |
The second term on the l.h.s. of (33) has the same form. Therefore, the latter may be eliminated by writing
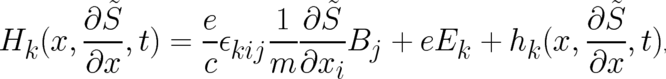 | (43) |
with 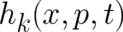 as our new unknown functions. They obey the simpler relations
as our new unknown functions. They obey the simpler relations
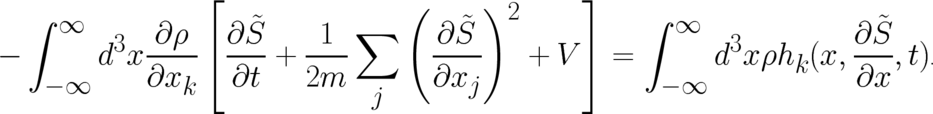 | (44) |
On a first look this condition for the allowed forces looks similar to the 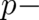 independent case [see (36)]. But
the dependence of
independent case [see (36)]. But
the dependence of 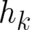 on
on 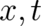 cannot be considered as ’given’ (externally controlled), as in
the
cannot be considered as ’given’ (externally controlled), as in
the 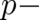 independent case, because it contains now the unknown
independent case, because it contains now the unknown 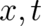 -dependence of the
derivatives of
-dependence of the
derivatives of 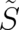 . We may nevertheless try to incorporate the r.h.s by adding a term
. We may nevertheless try to incorporate the r.h.s by adding a term 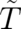 to
the bracket which depends on the derivatives of the multivalued quantity
to
the bracket which depends on the derivatives of the multivalued quantity 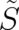 . This leads to the
condition
. This leads to the
condition
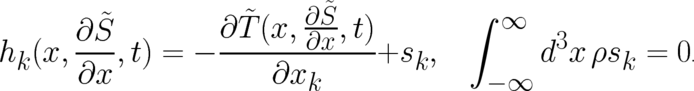 | (45) |
But this relation cannot be fulfilled for nontrivial 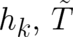 because the derivatives of
because the derivatives of 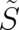 cannot be subject
to further constraints beyond those given by the differential equation; on top of that the derivatives with regard
to
cannot be subject
to further constraints beyond those given by the differential equation; on top of that the derivatives with regard
to 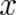 on the r.h.s. create higher order derivatives of
on the r.h.s. create higher order derivatives of 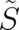 which are not present at the l.h.s. of Eq. (45).
The only possibility to fulfill this relation is for constant
which are not present at the l.h.s. of Eq. (45).
The only possibility to fulfill this relation is for constant 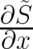 , a special case which has in fact
already be taken into account by adding the mechanical potential
, a special case which has in fact
already be taken into account by adding the mechanical potential 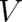 . We conclude that the
statistical constraint leads to
. We conclude that the
statistical constraint leads to 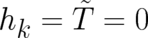 and that the statistical condition (44) takes the
form
and that the statistical condition (44) takes the
form
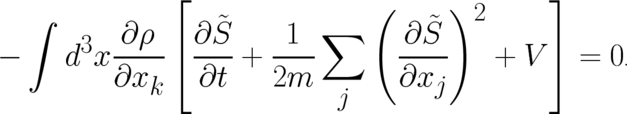 | (46) |
Thus, only a mechanical potential and the four electrodynamic potentials are compatible with the statistical constraint and will consequently - assuming that the present statistical approach reflects a fundamental principle of nature - be realized in nature. As is well known all existing interactions follow (sometimes in a generalized form) the gauge coupling scheme derived above. The statistical conditions imply not only Schrödinger’s equation but also the form of the (gauge) coupling to external influences and the form of the corresponding local force, the Lorentz force.
In the present derivation the usual order of proceeding is just inverted. In the conventional deterministic treatment the form of the local forces (Lorentz force), as taken from experiment, is used as a starting point. The potentials are introduced afterwards, in the course of a transition to a different formal framework (Lagrange formalism). In the present approach the fundamental assumptions are the statistical conditions. Then, taking into account an existing mathematical freedom (multi-valuedness of a variable) leads to the introduction of potentials. From these, the shape of the macroscopic (Lorentz) force can be derived, using the validity of the statistical conditions as a constraint.