5 Fisher information
In this section a local differential equation for 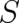 and
and 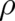 will be derived from the integral equation (46). As
our essential constraint we will use, besides general principles of simplicity (like homogeneity and isotropy of
space) the principle of maximal disorder, as realized by the requirement of minimal Fisher information. Using
the abbreviation
will be derived from the integral equation (46). As
our essential constraint we will use, besides general principles of simplicity (like homogeneity and isotropy of
space) the principle of maximal disorder, as realized by the requirement of minimal Fisher information. Using
the abbreviation
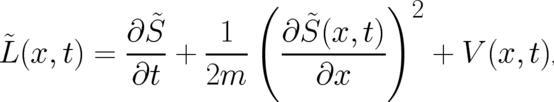 | (47) |
the general solution of (46) may be written in the form
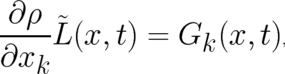 | (48) |
where the three functions 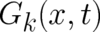 have to vanish upon integration over
have to vanish upon integration over 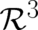 and are otherwise
arbitrary. If we restrict ourselves to an isotropic law, we may write
and are otherwise
arbitrary. If we restrict ourselves to an isotropic law, we may write
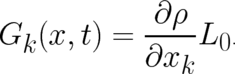 | (49) |
Then, our problem is to find a function 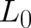 which fulfills the differential equation
which fulfills the differential equation
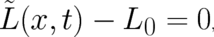 | (50) |
and condition (40). The method used in I for a one-dimensional situation, to determine 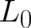 from the
requirement of minimal Fisher information, remains essentially unchanged in the present three-dimensional case.
The reader is referred to the detailed explanations reported in I.
from the
requirement of minimal Fisher information, remains essentially unchanged in the present three-dimensional case.
The reader is referred to the detailed explanations reported in I.
In I it has been shown that this principle of maximal disorder leads to an anomalous variational problem and
to the following conditions for our unknown function 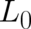 :
:
![( )
2
˜ ∂-ρ-- -∂---ρ---
L (x, t ) - L0 ρ, , = 0
∂ x ∂ x ∂ x
[ ( ) ]
∫
∂ ρ ∂ 2 ρ
δ d3x ρ L˜ (x, t) - L ρ, ----, --------- = 0,
0
∂ x ∂ x ∂ x](soq3dweb232x.png) |
(51)
(52)
|
where 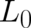 contains only derivatives of
contains only derivatives of 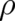 up to second order and does not explicitely depend on
up to second order and does not explicitely depend on
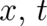 . If Eq. (51) is taken into account, the Euler-Lagrange equations of the variational problem (52) lead to
the following differential equation
. If Eq. (51) is taken into account, the Euler-Lagrange equations of the variational problem (52) lead to
the following differential equation
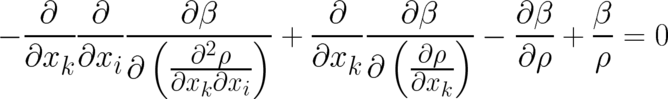 | (53) |
for the variable 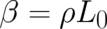 . Eq. (53) is a straightforward generalization of the corresponding
one-dimensional relation [equation (68) of I] to three spatial dimensions.
. Eq. (53) is a straightforward generalization of the corresponding
one-dimensional relation [equation (68) of I] to three spatial dimensions.
Besides (53) a further (consistency) condition exists, which leads to a simplification of the problem. The
function 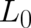 may depend on second order derivatives of
may depend on second order derivatives of 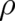 but this dependence must be of a special form
not leading to any terms in the Euler-Lagrange equations [according to (51) our final differential equation for
but this dependence must be of a special form
not leading to any terms in the Euler-Lagrange equations [according to (51) our final differential equation for
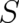 and
and 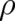 must not contain higher than second order derivatives of
must not contain higher than second order derivatives of 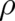 ]. Consequently, the first term in
Eq. (53) (as well as the sum of the remaining terms) has to vanish separately and (53) can be replaced by the
two equations
]. Consequently, the first term in
Eq. (53) (as well as the sum of the remaining terms) has to vanish separately and (53) can be replaced by the
two equations
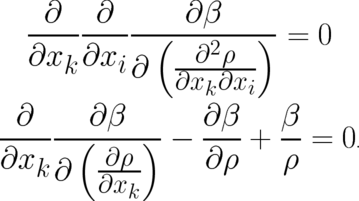 |
(54)
(55)
|
In I a new derivation of Fisher’s functional has been obtained, using the general solution of the
one-dimensional version of (53), as well as the so-called composition law. In the present three-dimensional
situation we set ourselves a less ambitious aim. We know that Fisher’s functional describes the maximal amount
of disorder. If we are able to find a solution of (54), (55) that agrees with this functional (besides ’null-terms’
giving no contribution to the Euler-Lagrange equations) then we will accept it as our correct solution. It is easy
to see that this solution is given by
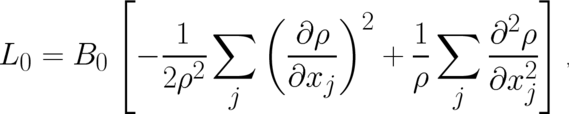 | (56) |
where 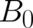 is an arbitrary constant. Eq. (56) presents again the three-dimensional (and isotropic)
generalization of the one-dimensional result obtained in I. By means of the identity
is an arbitrary constant. Eq. (56) presents again the three-dimensional (and isotropic)
generalization of the one-dimensional result obtained in I. By means of the identity
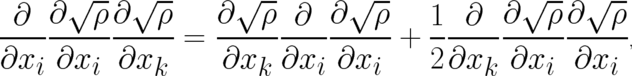 | (57) |
it is easily verified that the solution (56) obeys also condition (40). Using the decomposition (3) and renaming
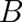 according to
according to 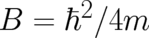 , the continuity equation (5) and the second differential
equation (51) respectively, take the form
, the continuity equation (5) and the second differential
equation (51) respectively, take the form
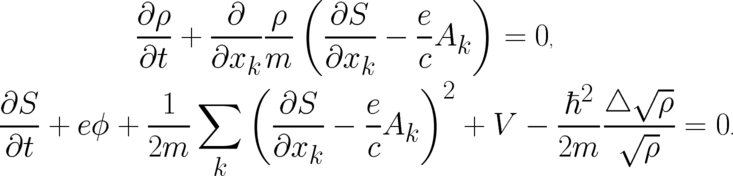 |
(58)
(59)
|
The function 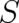 occurring in (58), (59) is single-valued but not unique (not gauge-invariant). If now
the complex-valued variable
occurring in (58), (59) is single-valued but not unique (not gauge-invariant). If now
the complex-valued variable
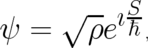 | (60) |
is introduced, the two equations (58), (59) may be written in compact form as real and imaginary parts of the
linear differential equation
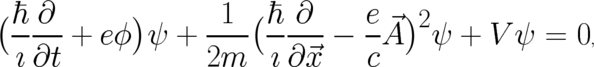 | (61) |
which completes our derivation of Schrödinger’s equation in the presence of a gauge field.
Eq. (61) is in manifest gauge-invariant form. The gauge-invariant derivatives of 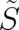 with respect to
with respect to 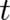 and
and
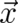 correspond to the two brackets in (61); in particular the canonical momentum
correspond to the two brackets in (61); in particular the canonical momentum 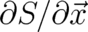 corresponds
to the momentum operator proportional to
corresponds
to the momentum operator proportional to 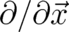 . Very frequently, Eq. (61) is written in the
form
. Very frequently, Eq. (61) is written in the
form
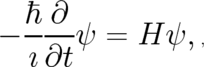 | (62) |
with the Hamilton operator
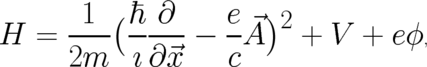 | (63) |
This quantity is very useful despite the fact that it contains, if applied to 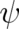 , only one of the two
gauge-invariant combinations present in the original time-dependent Schrödinger equation (61). The
operator (63) depends on the potentials
, only one of the two
gauge-invariant combinations present in the original time-dependent Schrödinger equation (61). The
operator (63) depends on the potentials 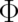 and
and 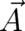 and is consequently a non-unique (not gauge-invariant)
mathematical object. The same is true for the time-development operator
and is consequently a non-unique (not gauge-invariant)
mathematical object. The same is true for the time-development operator 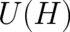 which is an operator
function of
which is an operator
function of 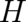 [20]. This non-uniqueness is a problem if
[20]. This non-uniqueness is a problem if 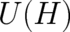 is interpreted as a quantity ruling the
time evolution of a single particle. It is no problem from the point of view of the statistical interpretation where
is interpreted as a quantity ruling the
time evolution of a single particle. It is no problem from the point of view of the statistical interpretation where
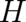 and
and 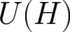 are primarily convenient mathematical objects which occur in a natural way if the
time-dependence of statistically relevant (uniquely defined) quantities, like expectation values and transition
probabilities, is to be calculated.
are primarily convenient mathematical objects which occur in a natural way if the
time-dependence of statistically relevant (uniquely defined) quantities, like expectation values and transition
probabilities, is to be calculated.
A fundamental ’static’ aspect of operators is their role as observables. The spectrum of eigenvalues of the
Hamilton operator 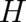 represents the set of all possible results of energy measurements of a single particle
(note that
represents the set of all possible results of energy measurements of a single particle
(note that 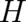 is nevertheless a quantity characterizing an observable property of an ensemble; no single
measurement result can be associated with
is nevertheless a quantity characterizing an observable property of an ensemble; no single
measurement result can be associated with 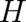 , only the measurement of the complete spectrum of
eigenvalues). In this sense the Hamilton operator corresponds to the classical Hamilton function
(and analogous relations are postulated for arbitrary classical observables). This correspondence is
obvious in the canonical quantization procedure. It is less obvious but nevertheless visible in the
present statistical approach as defined in section 2. The classical Hamilton function is implicitly
contained in the statistical conditions (6) and (7). The latter comprise the differential structure of the
canonical equations, which is itself determined by the Hamilton function. The formal details of the
relation between classical observables and operators in the present approach have still to be worked
out.
, only the measurement of the complete spectrum of
eigenvalues). In this sense the Hamilton operator corresponds to the classical Hamilton function
(and analogous relations are postulated for arbitrary classical observables). This correspondence is
obvious in the canonical quantization procedure. It is less obvious but nevertheless visible in the
present statistical approach as defined in section 2. The classical Hamilton function is implicitly
contained in the statistical conditions (6) and (7). The latter comprise the differential structure of the
canonical equations, which is itself determined by the Hamilton function. The formal details of the
relation between classical observables and operators in the present approach have still to be worked
out.
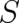 and
and 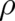 will be derived from the integral equation (46). As
our essential constraint we will use, besides general principles of simplicity (like homogeneity and isotropy of
space) the principle of maximal disorder, as realized by the requirement of minimal Fisher information. Using
the abbreviation
will be derived from the integral equation (46). As
our essential constraint we will use, besides general principles of simplicity (like homogeneity and isotropy of
space) the principle of maximal disorder, as realized by the requirement of minimal Fisher information. Using
the abbreviation
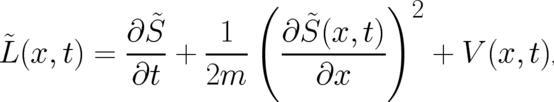
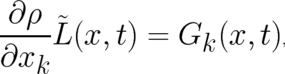
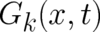 have to vanish upon integration over
have to vanish upon integration over  and are otherwise
arbitrary. If we restrict ourselves to an isotropic law, we may write
and are otherwise
arbitrary. If we restrict ourselves to an isotropic law, we may write
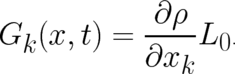
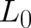 which fulfills the differential equation
which fulfills the differential equation
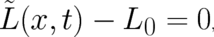
 from the
requirement of minimal Fisher information, remains essentially unchanged in the present three-dimensional case.
The reader is referred to the detailed explanations reported in I.
from the
requirement of minimal Fisher information, remains essentially unchanged in the present three-dimensional case.
The reader is referred to the detailed explanations reported in I.
 :
: ![( )
2
˜ ∂-ρ-- -∂---ρ---
L (x, t ) - L0 ρ, , = 0
∂ x ∂ x ∂ x
[ ( ) ]
∫
∂ ρ ∂ 2 ρ
δ d3x ρ L˜ (x, t) - L ρ, ----, --------- = 0,
0
∂ x ∂ x ∂ x](soq3dweb232x.png)
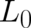 contains only derivatives of
contains only derivatives of 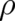 up to second order and does not explicitely depend on
up to second order and does not explicitely depend on
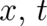 . If Eq. (51) is taken into account, the Euler-Lagrange equations of the variational problem (52) lead to
the following differential equation
. If Eq. (51) is taken into account, the Euler-Lagrange equations of the variational problem (52) lead to
the following differential equation
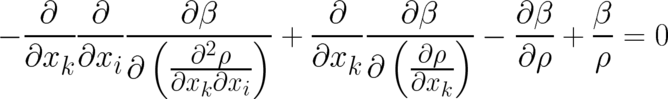
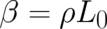 . Eq. (
. Eq. (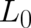 may depend on second order derivatives of
may depend on second order derivatives of 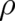 but this dependence must be of a special form
not leading to any terms in the Euler-Lagrange equations [according to (
but this dependence must be of a special form
not leading to any terms in the Euler-Lagrange equations [according to (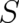 and
and 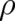 must not contain higher than second order derivatives of
must not contain higher than second order derivatives of 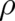 ]. Consequently, the first term in
Eq. (
]. Consequently, the first term in
Eq. (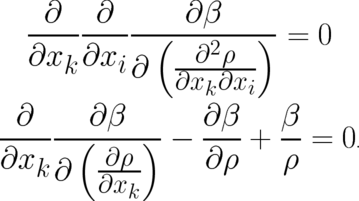
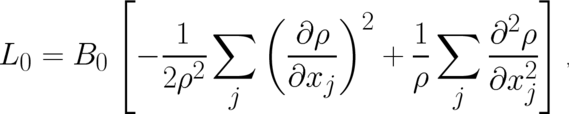
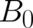 is an arbitrary constant. Eq. (
is an arbitrary constant. Eq. (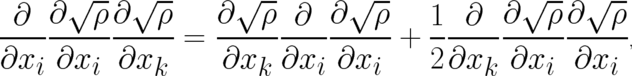
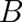 according to
according to 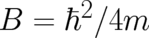 , the continuity equation (
, the continuity equation (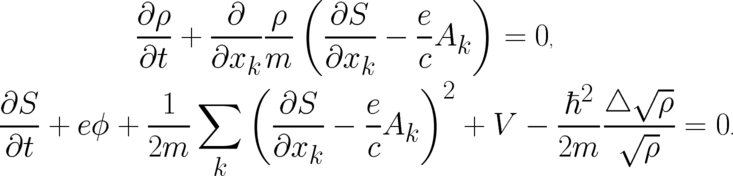
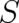 occurring in (58), (59) is single-valued but not unique (not gauge-invariant). If now
the complex-valued variable
occurring in (58), (59) is single-valued but not unique (not gauge-invariant). If now
the complex-valued variable
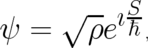
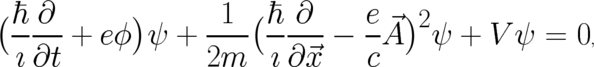
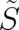 with respect to
with respect to 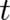 and
and
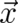 correspond to the two brackets in (
correspond to the two brackets in (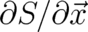 corresponds
to the momentum operator proportional to
corresponds
to the momentum operator proportional to 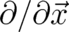 . Very frequently, Eq. (
. Very frequently, Eq. (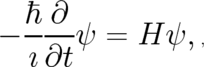
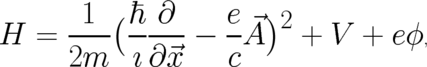
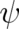 , only one of the two
gauge-invariant combinations present in the original time-dependent Schrödinger equation (
, only one of the two
gauge-invariant combinations present in the original time-dependent Schrödinger equation (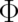 and
and 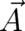 and is consequently a non-unique (not gauge-invariant)
mathematical object. The same is true for the time-development operator
and is consequently a non-unique (not gauge-invariant)
mathematical object. The same is true for the time-development operator 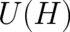 which is an operator
function of
which is an operator
function of 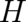
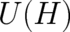 is interpreted as a quantity ruling the
time evolution of a single particle. It is no problem from the point of view of the statistical interpretation where
is interpreted as a quantity ruling the
time evolution of a single particle. It is no problem from the point of view of the statistical interpretation where
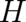 and
and 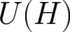 are primarily convenient mathematical objects which occur in a natural way if the
time-dependence of statistically relevant (uniquely defined) quantities, like expectation values and transition
probabilities, is to be calculated.
are primarily convenient mathematical objects which occur in a natural way if the
time-dependence of statistically relevant (uniquely defined) quantities, like expectation values and transition
probabilities, is to be calculated.
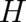 represents the set of all possible results of energy measurements of a single particle
(note that
represents the set of all possible results of energy measurements of a single particle
(note that 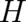 is nevertheless a quantity characterizing an observable property of an
is nevertheless a quantity characterizing an observable property of an 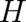 , only the measurement of the complete spectrum of
eigenvalues). In this sense the Hamilton operator corresponds to the classical Hamilton function
(and analogous relations are postulated for arbitrary classical observables). This correspondence is
obvious in the canonical quantization procedure. It is less obvious but nevertheless visible in the
present statistical approach as defined in section
, only the measurement of the complete spectrum of
eigenvalues). In this sense the Hamilton operator corresponds to the classical Hamilton function
(and analogous relations are postulated for arbitrary classical observables). This correspondence is
obvious in the canonical quantization procedure. It is less obvious but nevertheless visible in the
present statistical approach as defined in section