9 Discussion
In section 4 it as been shown that only the Lorentz force can exist as fundamental (quantum mechanical) force if
the statistical assumptions of section 3 are true. It is the only force (see however the remarks on spin
below) that can be incorporated in a ’standard’ differential equation for the dynamical variables
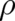 ,
, 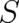 . The corresponding terms in the statistical field equations, representing the Lorentz
force, must be given by the familiar gauge (minimal) coupling terms containing the potentials. The
important fact that all forces in nature follow this ’principle of minimal coupling’ is commonly explained
as a consequence of local gauge invariance. The present treatment offers an alternative statistical
explanation.
. The corresponding terms in the statistical field equations, representing the Lorentz
force, must be given by the familiar gauge (minimal) coupling terms containing the potentials. The
important fact that all forces in nature follow this ’principle of minimal coupling’ is commonly explained
as a consequence of local gauge invariance. The present treatment offers an alternative statistical
explanation.
Let us use the following symbolic notation to represent the relation between the local force and the terms
representing its action in a statistical context:
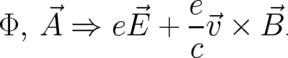 | (108) |
The fields 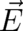 and
and 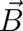 are uniquely defined in terms of the potentials
are uniquely defined in terms of the potentials 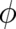 and
and 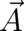 [see (30)] while the
inverse is not true. Roughly speaking, the local fields are ’derivatives’ of the potentials - and the potentials are
’integrals’ of the local field; this mathematical relation reflects the physical role of the potentials
[see (30)] while the
inverse is not true. Roughly speaking, the local fields are ’derivatives’ of the potentials - and the potentials are
’integrals’ of the local field; this mathematical relation reflects the physical role of the potentials
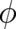 and
and 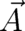 as statistical representatives of the the local fields
as statistical representatives of the the local fields 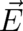 and
and 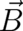 , as well as their
non-uniqueness. It might seem that the logical chain displayed in (108) is already realized in the classical
treatment of a particle-field system, where potentials have to be introduced in order to construct a
Lagrangian [21]. However, in this case, the form of the local force is not derived but postulated. The present
treatment ’explains’ the form of the Lagrangian - as a consequence of the basic assumptions listed in
section 3.
, as well as their
non-uniqueness. It might seem that the logical chain displayed in (108) is already realized in the classical
treatment of a particle-field system, where potentials have to be introduced in order to construct a
Lagrangian [21]. However, in this case, the form of the local force is not derived but postulated. The present
treatment ’explains’ the form of the Lagrangian - as a consequence of the basic assumptions listed in
section 3.
The generalization of the present theory to spin, reported in sections 6 and 7, leads to a correspondence
similar to Eq. (108), namely
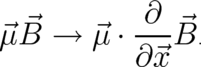 | (109) |
The term linear in 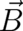 , on the l.h.s. of (109), plays the role of a ’potential’ for the local force on the r.h.s. All
points discussed after Eq. (108) apply here as well [As a matter of fact we consider
, on the l.h.s. of (109), plays the role of a ’potential’ for the local force on the r.h.s. All
points discussed after Eq. (108) apply here as well [As a matter of fact we consider 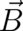 as a
unique physical quantity; it would not be unique if it would be defined in terms of the tensor on the
r.h.s. of (109)]. We see that the present approach allows for a certain unification of the usual gauge
and spin interaction terms - comparable with a relativistic formulation, where the spin coupling
is introduced simultaneously with the other gauge coupling terms. Unfortunately, the derivation
of the spin force on the r.h.s. of (109) differs from the derivation of the Lorentz force insofar as
additional assumptions had to be made in order to arrive at the final result (see the remarks in
section 7).
as a
unique physical quantity; it would not be unique if it would be defined in terms of the tensor on the
r.h.s. of (109)]. We see that the present approach allows for a certain unification of the usual gauge
and spin interaction terms - comparable with a relativistic formulation, where the spin coupling
is introduced simultaneously with the other gauge coupling terms. Unfortunately, the derivation
of the spin force on the r.h.s. of (109) differs from the derivation of the Lorentz force insofar as
additional assumptions had to be made in order to arrive at the final result (see the remarks in
section 7).
Our notation for potentials 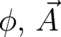 , fields
, fields 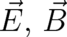 , and parameters
, and parameters 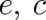 suggests that these
quantities are electrodynamical in nature. However, this is not necessarily true. The constraint (31) yields four
equations which are not sufficient to determine the six fields
suggests that these
quantities are electrodynamical in nature. However, this is not necessarily true. The constraint (31) yields four
equations which are not sufficient to determine the six fields 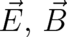 ; additional conditions must be imposed.
The most familiar possibility is, of course, the second pair of Maxwell’s equations leading to the
electrodynamical gauge field. A second possible realization for the fields
; additional conditions must be imposed.
The most familiar possibility is, of course, the second pair of Maxwell’s equations leading to the
electrodynamical gauge field. A second possible realization for the fields 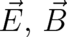 is given by the inertial
forces acting on a mass
is given by the inertial
forces acting on a mass 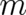 in an arbitrarily accelerated reference frame [15]. In Appendix A a brief
discussion of the inertial gauge field and its interplay with the Maxwell field is given. It is remarkable that the
present theory establishes a (admittedly somewhat vague) link between the two extremely separated
physical fields of inertia and quantum theory. An interesting point is that the mathematical axioms of
in an arbitrarily accelerated reference frame [15]. In Appendix A a brief
discussion of the inertial gauge field and its interplay with the Maxwell field is given. It is remarkable that the
present theory establishes a (admittedly somewhat vague) link between the two extremely separated
physical fields of inertia and quantum theory. An interesting point is that the mathematical axioms of
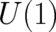 gauge theory imply the Maxwell field but say nothing about the inertial field which is just as
real as the former. The inertial field
gauge theory imply the Maxwell field but say nothing about the inertial field which is just as
real as the former. The inertial field 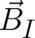 [see (114)] may also lead to a spin response of the
ensemble. Experiments to verify such inertial effects of spin have been proposed by Mashhoon and
Kaiser [25].
[see (114)] may also lead to a spin response of the
ensemble. Experiments to verify such inertial effects of spin have been proposed by Mashhoon and
Kaiser [25].
It is generally assumed that the electrodynamic potentials have a particular significance in quantum
mechanics which they do not have in classical physics. Let us analyze this statement in detail. (we restrict
ourselves in the following discussion to the electrodynamical gauge field). The first part of this statement,
concerning the significance of the potentials, is of course true. The second part of the statement,
asserting that in classical physics all external influences can be described solely in terms of field
strengths, is wrong. More precisely, it is true for classical mechanics but not for classical physics in
general. A counterexample - a theory belonging to classical physics but with potentials playing an
indispensable role - is provided by the classical limit (104),(105) of Schrödinger’s equation. In this field
theory the potentials play an indispensable role because (in contrast to particle theories, like the
canonical equations) no further derivatives of the Hamiltonian, which could restore the fields, are to be
performed. This means that the significance of the potentials is not restricted to quantum theory
but rather holds for the whole class of statistical theories discussed above, which contains both
quantum theory and its classical limit theory as special cases. This result is in agreement with the
present interpretation of the potentials as statistical representatives of the local fields of particle
physics.
The precise characterization of the role of the potentials is important for the interpretation of the
Aharonov-Bohm effect. The ’typical quantum-mechanical features’ observed in these phase shift experiments
should be identified by comparing the quantum mechanical results not with classical mechanics but with
the predictions of the classical statistical theory (104),(105). The predictions of two statistical
theories, both of which use potentials to describe the influence of the external field, have to be
compared.
The interpretation of a physical theory is commonly considered as a matter that cannot be described
by mathematical means. This may be generally true, but nevertheless mathematical facts exist
which have an immediate bearing on questions of interpretation. The most important of these is
probably the limiting behavior of a theory. The fact that the classical limit of quantum mechanics -
discussed in section 8 - is not classical mechanics but a special (configuration space) classical statistical
theory is widely unknown. This lack of knowledge is one of the main reasons for the widespread
erroneous belief that quantum mechanics can be used to describe the dynamics of individual particles.
Unfortunately, this erroneous belief is historically grown and firmly established in our thinking
as shown by the ubiquitous use of phrases like ’the wave function of the electron’ or ’quantum
mechanics’.
It is clear that an erroneous identification of the domain of validity of a physical theory will automatically
create all kinds of mysteries, ill-posed questions and unsolvable problems. Above, we have identified one of
the more subtle problems of this kind, concerning the role of potentials in quantum mechanics (a
paradigmatic example is the ’measurement problem’ which is unsolved since its creation eighty years
ago). Generalizing the above argumentation concerning potentials, we claim that characteristic
features of quantum theory cannot be identified by comparison with classical mechanics. Instead,
quantum theory should be compared with its classical limit, which is in the present 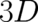 -case
given by (104), (105). The latter theory is probably much more difficult to solve (numerically)
than Schrödinger’s equation because is is no longer linear in
-case
given by (104), (105). The latter theory is probably much more difficult to solve (numerically)
than Schrödinger’s equation because is is no longer linear in 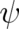 . Nevertheless, it would be very
interesting to compare the solutions of (104), (105) with those of (58), (59) to find out which ’typical
quantum-theoretic features’ are already given by statistical (nonlocal) correlations of the classical limit
theory and which features are really quantum-theoretical in nature - related to the nonzero value of
. Nevertheless, it would be very
interesting to compare the solutions of (104), (105) with those of (58), (59) to find out which ’typical
quantum-theoretic features’ are already given by statistical (nonlocal) correlations of the classical limit
theory and which features are really quantum-theoretical in nature - related to the nonzero value of
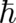 .
.
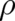 ,
, 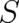 . The corresponding terms in the statistical field equations, representing the Lorentz
force, must be given by the familiar gauge (minimal) coupling terms containing the potentials. The
important fact that all forces in nature follow this ’principle of minimal coupling’ is commonly explained
as a consequence of local gauge invariance. The present treatment offers an alternative statistical
explanation.
. The corresponding terms in the statistical field equations, representing the Lorentz
force, must be given by the familiar gauge (minimal) coupling terms containing the potentials. The
important fact that all forces in nature follow this ’principle of minimal coupling’ is commonly explained
as a consequence of local gauge invariance. The present treatment offers an alternative statistical
explanation.
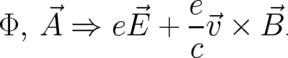
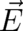 and
and 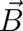 are uniquely defined in terms of the potentials
are uniquely defined in terms of the potentials 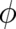 and
and 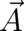 [see (
[see (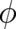 and
and 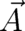 as statistical representatives of the the local fields
as statistical representatives of the the local fields 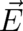 and
and 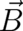 , as well as their
non-uniqueness. It might seem that the logical chain displayed in (
, as well as their
non-uniqueness. It might seem that the logical chain displayed in (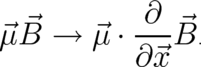
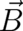 , on the l.h.s. of (
, on the l.h.s. of (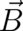 as a
unique physical quantity; it would not be unique if it would be defined in terms of the tensor on the
r.h.s. of (
as a
unique physical quantity; it would not be unique if it would be defined in terms of the tensor on the
r.h.s. of (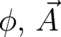 , fields
, fields 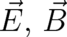 , and parameters
, and parameters 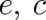 suggests that these
quantities are electrodynamical in nature. However, this is not necessarily true. The constraint (
suggests that these
quantities are electrodynamical in nature. However, this is not necessarily true. The constraint (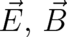 ; additional conditions must be imposed.
The most familiar possibility is, of course, the second pair of Maxwell’s equations leading to the
electrodynamical gauge field. A second possible realization for the fields
; additional conditions must be imposed.
The most familiar possibility is, of course, the second pair of Maxwell’s equations leading to the
electrodynamical gauge field. A second possible realization for the fields 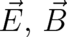 is given by the
is given by the 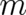 in an arbitrarily accelerated reference frame
in an arbitrarily accelerated reference frame 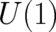 gauge theory imply the Maxwell field but say nothing about the inertial field which is just as
real as the former. The inertial field
gauge theory imply the Maxwell field but say nothing about the inertial field which is just as
real as the former. The inertial field 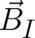 [see (
[see (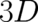 -case
given by (
-case
given by (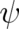 . Nevertheless, it would be very
interesting to compare the solutions of (
. Nevertheless, it would be very
interesting to compare the solutions of (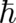 .
.