 particles with spin in an external gauge field, means to derive essentially the whole of
non-relativistic QT.
particles with spin in an external gauge field, means to derive essentially the whole of
non-relativistic QT.
Quantum theory (QT) may either be defined by a set of axioms or otherwise be ’derived’ from classical physics
by using certain assumptions. Today, QT is frequently identified with a set of axioms defining a Hilbert space
structure. This mathematical structure has been created (by von Neumann) by abstraction from the linear
solution space of the central equation of QT, the Schrödinger equation. Thus, deriving Schrödinger’s equation is
basically the same as deriving QT. To derive the most general version of the time-dependent Schrödinger
equation, describing  particles with spin in an external gauge field, means to derive essentially the whole of
non-relativistic QT.
particles with spin in an external gauge field, means to derive essentially the whole of
non-relativistic QT.
The second way of proceeding is sometimes called ’quantization’. In the standard (canonical) quantization method one starts from a classical Hamiltonian whose basic variables are then ’transformed’, by means of well-known correspondence rules,
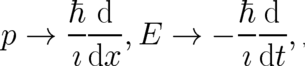 | (1) |
into operators. Then, all relevant classical observables may be rewritten as operators acting on states of a Hilbert space etc; the details of the ’derivation’ of Schrödinger’s equation along this lines may be found in many textbooks. There are formal problems with this approach which have been identified many years ago, and can be expressed e.g. in terms of Groenewold’s theorem, see [21], [18]. Even more seriously, there is no satisfactory explanation for this ’metamorphosis’ of observables into operators. This quantization method (as well as several other mathematically more sophisticated versions of it) is just a recipe or, depending on one’s taste, ”black magic”, [24]. Note that the enormous success of this recipe in various contexts - including field quantization - is no substitute for an explanation.
The choice of a particular quantization procedure will be strongly influenced by the preferred interpretation of the quantum theoretical formalism. If QT is interpreted as a theory describing individual events, then the Hamiltonian of classical mechanics becomes a natural starting point. This ’individuality assumption’ is an essential part of the dominating ’conventional’, or ’Copenhagen’, interpretation (CI) of QT. It is well-known, that QT becomes a source of mysteries and paradoxes 1 whenever it is interpreted in the sense of CI, as a (complete) theory for individual events. Thus, the canonical quantization method and the CI are similar in two respects: both rely heavily on the concept of individual particles and both are rather mysterious.
This situation confronts us with a fundamental alternative. Should we accept the mysteries and paradoxes as inherent attributes of reality or should we not, instead, critically reconsider our assumptions, in particular the ’individuality assumption’. As a matter of fact, the dynamical numerical output of quantum mechanics consists of probabilities. A probability is a ”deterministic” prediction which can be verified in a statistical sense only, i.e. by performing experiments on a large number of identically prepared individual systems, see [9], [44]. Therefore, the very structure of QT tells us that it is a theory about statistical ensembles only, see [6]. If dogmatic or philosophical reasons ’force’ us to interpret QT as a theory about individual events, we have to create complicated intellectual constructs, which are not part of the physical formalism, and lead to unsolved problems and contradictions.
The present author believes, like several other physicists [see e.g. [29, 14, 43, 10, 6, 8, 56, 71, 48, 51, 67, 66, 35, 2]] that QT is a purely statistical theory whose predictions can only be used to describe the behavior of statistical ensembles and not of individual particles. This statistical interpretation (SI) of QT eliminates all mysteries and paradoxes - and this shows that the mysteries and paradoxes are not part of QT itself but rather the result of a particular (mis)interpretation of QT. In view of the similarity discussed above, we adopt the statistical point of view, not only for the interpretation of QT itself, but also in our search for quantization conditions. The general strategy is to find a new set of (as) simple (as possible) statistical assumptions which can be understood in physical terms and imply QT. Such an approach would also provide an explanation for the correspondence rules (1).
The present paper belongs to a series of works aimed at such an explanation. Quite generally, the present work continues a long tradition of attempts, see [61, 47, 59, 55, 16, 40, 22, 17], to characterize QT by mathematical relations which can be understood in physical terms2 (in contrast to the axiomatic approach). More specifically, it continues previous attempts to derive Schrödinger’s equation with the help of statistical concepts, see [23], [53, 64], [32]. These works, being quite different in detail, share the common feature that a statistical ensemble and not a particle Hamiltonian is used as a starting point for quantization. Finally, in a previous work, [33], of the present author an attempt has been undertaken to construct a complete statistical approach to QT with the help of a small number of very simple (statistical) assumptions. This work will be referred to as I. The present paper is a continuation and extension of I.
The quantization method reported in I is based on the following general ideas:
These general ideas lead to the mathematical assumptions which represent the basis for the treatment reported
in I. This work was restricted to a one-dimensional configuration space (a single particle ensemble with a single
spatial degree of freedom). The present work generalizes the treatment of I to a 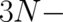 dimensional
configuration space ( ensembles representing an arbitrary number
dimensional
configuration space ( ensembles representing an arbitrary number 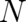 of particles allowed to move in
three-dimensional space), gauge-coupling, and spin. In a first step the generalization to three spatial dimensions
is performed; the properly generalized basic relations are reported in section 2. This section contains also a
review of the fundamental ideas.
of particles allowed to move in
three-dimensional space), gauge-coupling, and spin. In a first step the generalization to three spatial dimensions
is performed; the properly generalized basic relations are reported in section 2. This section contains also a
review of the fundamental ideas.
In section 3 we make use of a mathematical freedom, which is already contained in our basic assumptions,
namely the multi-valuedness of the variable 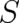 . This leads to the appearance of potentials in statistical
relations replacing the local forces of single-event (mechanical) theories. The mysterious non-local action of the
vector potential (in effects of the Aharonov-Bohm type) is explained as a consequence of the statistical nature of
QT. In section 4 we discuss a related question: Which constraints on admissible forces exist for the
present class of statistical theories ? The answer is that only macroscopic (elementary) forces of
the form of the Lorentz force can occur in nature, because only these survive the transition to
QT . These forces are statistically represented by potentials, i.e. by the familiar gauge coupling
terms in matter field equations. The present statistical approach provides a natural explanation
for the long-standing question why potentials play an indispensable role in the field equations of
physics.
. This leads to the appearance of potentials in statistical
relations replacing the local forces of single-event (mechanical) theories. The mysterious non-local action of the
vector potential (in effects of the Aharonov-Bohm type) is explained as a consequence of the statistical nature of
QT. In section 4 we discuss a related question: Which constraints on admissible forces exist for the
present class of statistical theories ? The answer is that only macroscopic (elementary) forces of
the form of the Lorentz force can occur in nature, because only these survive the transition to
QT . These forces are statistically represented by potentials, i.e. by the familiar gauge coupling
terms in matter field equations. The present statistical approach provides a natural explanation
for the long-standing question why potentials play an indispensable role in the field equations of
physics.
In section 5 it is shown that among all statistical theories only the time-dependent Schrödinger equation follows
the logical requirement of maximal disorder or minimal Fisher information. Spin one-half is introduced, in
section 6, as the property of a statistical ensemble to respond to an external gauge field in two different ways. A
generalized calculation, reported in sections 6 and 7, leads to Pauli’s (single-particle) equation. In section 8 an
alternative derivation, following [5], and [19] is reported, which is particularly convenient for the generalization
to arbitrary 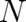 . The latter is performed in section 9, which completes our statistical derivation of
non-relativistic QT.
. The latter is performed in section 9, which completes our statistical derivation of
non-relativistic QT.
In section 10 the classical limit of QT is studied and it is stressed that the classical limit of QT is not classical mechanics but a classical statistical theory. In section 11 various questions related to the present approach, including the role of potentials and the interpretation of QT, are discussed. The final section 12 contains a short summary and mentions a possible direction for future research.