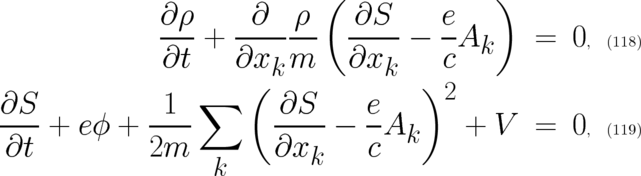
The classical limit of Schrödinger’s equation plays an important role for two topics discussed in the next section, namely the interpretation of QT and the particular significance of potentials in QT; to study these questions it is sufficient to consider a single-particle ensemble described by a single state function. This ’classical limit theory’ is given by the two differential equations
which are obtained from Eqs. (50) and (51) by performing the limit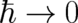 . The quantum
mechanical theory (50) and (51) and the classical theory (118) and (119) show fundamentally the same
mathematical structure; both are initial value problems for the variables
. The quantum
mechanical theory (50) and (51) and the classical theory (118) and (119) show fundamentally the same
mathematical structure; both are initial value problems for the variables 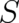 and
and 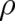 obeying two partial
differential equations. The difference is the absence of the last term on the l.h.s. of (51) in the
corresponding classical equation (119). This leads to a decoupling of
obeying two partial
differential equations. The difference is the absence of the last term on the l.h.s. of (51) in the
corresponding classical equation (119). This leads to a decoupling of 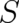 and
and 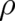 in (119); the identity
of the classical object described by
in (119); the identity
of the classical object described by 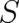 is no longer affected by statistical aspects described by
is no longer affected by statistical aspects described by
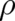 .
.
The field theory (118), (119) for the two ’not decoupled’ fields 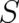 and
and 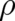 is obviously very different from
classical mechanics which is formulated in terms of trajectories. The fact that one of these equations,
namely (119), agrees with the Hamilton-Jacobi equation, does not change the situation since the presence of the
continuity equation (118) cannot be neglected. On top of that, even if it could be neglected, Eq. (119) would
still be totally different from classical mechanics: In order to construct particle trajectories from the partial
differential equation (119) for the field
is obviously very different from
classical mechanics which is formulated in terms of trajectories. The fact that one of these equations,
namely (119), agrees with the Hamilton-Jacobi equation, does not change the situation since the presence of the
continuity equation (118) cannot be neglected. On top of that, even if it could be neglected, Eq. (119) would
still be totally different from classical mechanics: In order to construct particle trajectories from the partial
differential equation (119) for the field 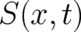 , a number of clearly defined mathematical
manipulations, which are part of the classical theory of canonical transformations, see [20], must be
performed. The crucial point is that the latter theory is not part of QT and cannot be added ’by hand’
in the limit
, a number of clearly defined mathematical
manipulations, which are part of the classical theory of canonical transformations, see [20], must be
performed. The crucial point is that the latter theory is not part of QT and cannot be added ’by hand’
in the limit 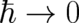 . Thus, (118), (119) is, like QT, an indeterministic theory predicting
not values of single event observables but only probabilities, which must be verified by ensemble
measurements.
. Thus, (118), (119) is, like QT, an indeterministic theory predicting
not values of single event observables but only probabilities, which must be verified by ensemble
measurements.
Given that we found a solution 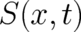 ,
, 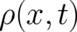 of (118), (119) for given initial values, we may ask
which experimental predictions can be made with the help of these quantities. Using the fields
of (118), (119) for given initial values, we may ask
which experimental predictions can be made with the help of these quantities. Using the fields
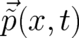 ,
, 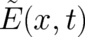 defined by Eqs. (19), (18), the Hamilton-Jacobi equation (119) takes the
form
defined by Eqs. (19), (18), the Hamilton-Jacobi equation (119) takes the
form
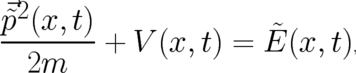 | (120) |
The l.h.s. of (120) depends on the field 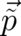 in the same way as a classical particle Hamiltonian on the
(gauge-invariant) kinetic momentum
in the same way as a classical particle Hamiltonian on the
(gauge-invariant) kinetic momentum 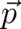 . We conclude that the field
. We conclude that the field 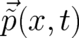 describes a mapping from
space-time points to particle momenta: If a particle (in an external electromagnetic field) is found at time
describes a mapping from
space-time points to particle momenta: If a particle (in an external electromagnetic field) is found at time 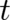 at
the point
at
the point 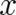 , then its kinetic momentum is given by
, then its kinetic momentum is given by 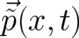 . This is not a deterministic prediction
since we can not predict if a single particle will be or will not be at time
. This is not a deterministic prediction
since we can not predict if a single particle will be or will not be at time 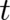 at point
at point 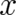 ; the
present theory gives only a probability
; the
present theory gives only a probability 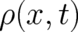 for such an event. Combining our findings
about
for such an event. Combining our findings
about 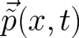 and
and 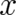 we conclude that the experimental prediction which can be made
with the help of
we conclude that the experimental prediction which can be made
with the help of 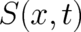 ,
, 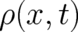 is given by the following phase space probability
density:
is given by the following phase space probability
density:
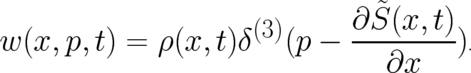 | (121) |
Eq. (121) confirms our claim that the classical limit theory is a statistical theory. The one-dimensional version of (121) has been obtained before by means of a slightly different method in I. The deterministic element [realized by the delta-function shaped probability in (121)] contained in the classical statistical theory (118), (119) is absent in QT, see I.
Eqs. (118), (119) constitute the mathematically well-defined limit 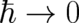 of Schrödinger’s equation.
Insofar as there is general agreement with regard to two points, namely that (i) ’non-classicality’ (whatever this
may mean precisely) is expressed by a nonzero
of Schrödinger’s equation.
Insofar as there is general agreement with regard to two points, namely that (i) ’non-classicality’ (whatever this
may mean precisely) is expressed by a nonzero 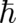 , and that (ii) Schrödinger’s equation is the most important
relation of quantum theory, one would also expect general agreement with regard to a further point, namely that
Eqs. (118), (119) present essentially (for a three-dimensional configuration space) the classical
limit of quantum mechanics. But this is, strangely enough, not the case. With a few exceptions,
see [68], [59], [7], [62], [32], most works (too many to be quoted) take it for granted that the classical limit of
quantum theory is classical mechanics. The objective of papers like [57], [69], [37], [3] devoted to “..the
classical limit of quantum mechanics..“ is very often not the problem: ”what is the classical limit
of quantum mechanics ?” but rather: “how to bridge the gap between quantum mechanics and
classical mechanics ?”. Thus, the fact that classical mechanics is the classical limit of quantum
mechanics is considered as evident and any facts not compatible with it - like Eqs. (118), (119) - are
denied.
, and that (ii) Schrödinger’s equation is the most important
relation of quantum theory, one would also expect general agreement with regard to a further point, namely that
Eqs. (118), (119) present essentially (for a three-dimensional configuration space) the classical
limit of quantum mechanics. But this is, strangely enough, not the case. With a few exceptions,
see [68], [59], [7], [62], [32], most works (too many to be quoted) take it for granted that the classical limit of
quantum theory is classical mechanics. The objective of papers like [57], [69], [37], [3] devoted to “..the
classical limit of quantum mechanics..“ is very often not the problem: ”what is the classical limit
of quantum mechanics ?” but rather: “how to bridge the gap between quantum mechanics and
classical mechanics ?”. Thus, the fact that classical mechanics is the classical limit of quantum
mechanics is considered as evident and any facts not compatible with it - like Eqs. (118), (119) - are
denied.
What, then, is the reason for this widespread denial of reality ? One of the main reasons is the principle of
reductionism which still rules the thinking of most physicists today. The reductionistic ideal is a hierarchy of
physical theories; better theories have an enlarged domain of validity and contain ’inferior’ theories as special
cases. This principle which has been extremely successful in the past dictates that classical mechanics is a special
case of quantum theory. Successful as this idea might have been during a long period of time it
is not necessarily universally true; quantum mechanics and classical mechanics describe different
domains of reality, both may be true in their own domains of validity. Many phenomena in nature
indicate that the principle of reductionism (alone) is insufficient to describe reality, see [38]. Releasing
ourselves from the metaphysical principle of reductionism, we accept that the classical limit of
quantum mechanics for a three-dimensional configuration space is the statistical theory defined by
Eqs. (118), (119). It is clear that this theory is not realized in nature (with the same physical meaning of the
variables) because 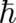 is different from zero. But this is a different question and does not affect the
conclusion.
is different from zero. But this is a different question and does not affect the
conclusion.