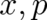 ; each case
has to be investigated separately. Thus, the breakdown of (1), as expressed by Groenewold’s theorem, is no
surprise.
; each case
has to be investigated separately. Thus, the breakdown of (1), as expressed by Groenewold’s theorem, is no
surprise.
In this paper it has been shown, continuing the work of I, that the basic differential equation of non-relativistic QT may be derived from a number of clearly defined assumptions of a statistical nature. Although this does not exclude the possibility of other derivations, we consider this success as a strong argument in favor of the statistical interpretation of QT.
This result explains also, at least partly, the success of the canonical quantization rules (1). Strictly
speaking, these rules have only be derived for a particular (though very important) special case, the
Hamiltonian. However, one can expect that (1) can be verified for all meaningful physical
observables4 .
On the other hand, it cannot be expected that the rules (1) hold for arbitrary functions of 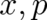 ; each case
has to be investigated separately. Thus, the breakdown of (1), as expressed by Groenewold’s theorem, is no
surprise.
; each case
has to be investigated separately. Thus, the breakdown of (1), as expressed by Groenewold’s theorem, is no
surprise.
The fundamental Ehrenfest-like relations of the present theory establish [like the formal rules (1)] a correspondence between particle mechanics and QT. Today, philosophical questions concerning, in particular, the ’reality’ of particles play an important role in the thinking of some physicists. So: ’What is this theory about.. ?’ While the present author is no expert in this field, the concept of indeterminism, as advocated by the philosopher [52], seems to provide an appropriate philosophical basis for the present work.
The present method to introduce gauge fields by means of a multi-valued dynamic variable (’phase function’) has
been invented many years ago but leads, in the context of the present statistical theory, nevertheless to several
new results. In particular, it has been shown in section 3, that only the Lorentz force can exist as fundamental
macroscopic force if the statistical assumptions of section 2 are valid. It is the only force (in the absence of spin
effects, see the remarks below) that can be incorporated in a ’standard’ differential equation for the dynamical
variables 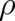 ,
, 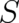 . The corresponding terms in the statistical field equations, representing the Lorentz
force, are given by the familiar gauge (minimal) coupling terms containing the potentials. The
important fact that all forces in nature follow this ’principle of minimal coupling’ is commonly
explained as a consequence of local gauge invariance. The present treatment offers an alternative
explanation.
. The corresponding terms in the statistical field equations, representing the Lorentz
force, are given by the familiar gauge (minimal) coupling terms containing the potentials. The
important fact that all forces in nature follow this ’principle of minimal coupling’ is commonly
explained as a consequence of local gauge invariance. The present treatment offers an alternative
explanation.
Let us use the following symbolic notation to represent the relation between the local force and the terms representing its action in a statistical context:
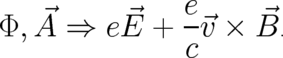 | (122) |
The fields 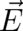 and
and 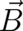 are uniquely defined in terms of the potentials
are uniquely defined in terms of the potentials 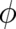 and
and 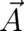 [see (23)] while the
inverse is not true. Roughly speaking, the local fields are ’derivatives’ of the potentials - and the potentials are
’integrals’ of the local field; this mathematical relation reflects the physical role of the potentials
[see (23)] while the
inverse is not true. Roughly speaking, the local fields are ’derivatives’ of the potentials - and the potentials are
’integrals’ of the local field; this mathematical relation reflects the physical role of the potentials 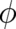 and
and 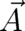 as statistical representatives of the the local fields
as statistical representatives of the the local fields 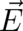 and
and 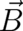 , as well as their non-uniqueness. It might
seem that the logical chain displayed in (122) is already realized in the classical treatment of a
particle-field system, where potentials have to be introduced in order to construct a Lagrangian, see
e.g. [36]. However, in this case, the form of the local force is not derived but postulated. The present
treatment ’explains’ the form of the Lagrangian - as a consequence of the basic assumptions listed in
section 2.
, as well as their non-uniqueness. It might
seem that the logical chain displayed in (122) is already realized in the classical treatment of a
particle-field system, where potentials have to be introduced in order to construct a Lagrangian, see
e.g. [36]. However, in this case, the form of the local force is not derived but postulated. The present
treatment ’explains’ the form of the Lagrangian - as a consequence of the basic assumptions listed in
section 2.
The generalization of the present theory to spin, reported in sections 6 and 7, leads to a correspondence similar to Eq. (122), namely
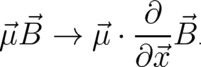 | (123) |
The term linear in 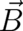 , on the l.h.s. of (123), plays the role of a ’potential’ for the local force on the r.h.s. The
points discussed after Eq. (122) apply here as well [As a matter of fact we consider
, on the l.h.s. of (123), plays the role of a ’potential’ for the local force on the r.h.s. The
points discussed after Eq. (122) apply here as well [As a matter of fact we consider 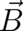 as a unique physical
quantity; it would not be unique if it would be defined in terms of the tensor on the r.h.s. of (123)]. We see here
a certain analogy between gauge and spin interaction terms. Unfortunately, the derivation of the spin force on
the r.h.s. of (123) requires - in contrast to the Lorentz force - additional assumptions (see the remarks in
sections 7, 8).
as a unique physical
quantity; it would not be unique if it would be defined in terms of the tensor on the r.h.s. of (123)]. We see here
a certain analogy between gauge and spin interaction terms. Unfortunately, the derivation of the spin force on
the r.h.s. of (123) requires - in contrast to the Lorentz force - additional assumptions (see the remarks in
sections 7, 8).
Our notation for potentials 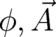 , fields
, fields 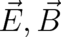 , and parameters
, and parameters 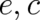 suggests that these
quantities are electrodynamical in nature. However, this is not necessarily true. By definition, the
fields
suggests that these
quantities are electrodynamical in nature. However, this is not necessarily true. By definition, the
fields 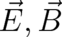 obey four equations (the homogeneous Maxwell equations), which means that
additional conditions are required in order to determine these six fields. The most familiar possibility
is, of course, the second pair of Maxwell’s equations. A second possible realization for the fields
obey four equations (the homogeneous Maxwell equations), which means that
additional conditions are required in order to determine these six fields. The most familiar possibility
is, of course, the second pair of Maxwell’s equations. A second possible realization for the fields
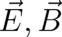 is given by the inertial forces acting on a mass
is given by the inertial forces acting on a mass 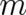 in an arbitrarily accelerated reference
frame, see [27]. The inertial gauge field may also lead to a spin response of the ensemble; such
experiments have been proposed by [45]. It is remarkable that the present theory establishes a
(admittedly somewhat vague) link between the two extremely separated physical fields of inertia and
QT.
in an arbitrarily accelerated reference
frame, see [27]. The inertial gauge field may also lead to a spin response of the ensemble; such
experiments have been proposed by [45]. It is remarkable that the present theory establishes a
(admittedly somewhat vague) link between the two extremely separated physical fields of inertia and
QT.
It is generally assumed that the electrodynamic potentials have a particular significance in QT which they do not have in classical physics. Let us analyze this statement in detail. The first part of the statement, concerning the significance of the potentials, is of course true. The second part, asserting that in classical physics all external influences can be described solely in terms of field strengths, is wrong. More precisely, it is true for classical mechanics but not for classical physics in general. A counterexample - a theory belonging to classical physics but with potentials playing an indispensable role - is provided by the classical limit (118),(119) of Schrödinger’s equation. In this field theory the potentials play an indispensable role because (in contrast to particle theories, like the canonical equations) no further derivatives of the Hamiltonian, which could restore the fields, are to be performed. This means that the significance of the potentials is not restricted to quantum theory but rather holds for the whole class of statistical theories discussed above, which contains both quantum theory and its classical limit theory as special cases. This result is in agreement with the statistical interpretation of potentials proposed in section 3.
The precise characterization of the role of the potentials is of particular importance for the interpretation of the Aharonov-Bohm effect. The ’typical quantum-mechanical features’ observed in these phase shift experiments should be identified by comparing the quantum mechanical results not with classical mechanics but with the predictions of the classical statistical theory (118), (119). The predictions of two statistical theories, both of which use potentials to describe the influence of the external field, have to be compared.
The limiting behavior of Schrödinger’s equation as 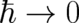 , discussed in section 10, is very important for
the proper interpretation of QT. The erronous belief (wish) that this limit can (must) be identified with classical
mechanics is closely related to the erroneous belief that QT is able to describe the dynamics of individual
particles. In this respect QT is obviously an incomplete theory, as has been pointed out many times before,
during the last eighty years, see e.g. [15], [43] , [6], [25]. Unfortunately, this erroneous opinion is historically
grown and firmly established in our thinking as shown by the ubiquitous use of phrases like ’the wave
function of the electron’. But it is clear that an erroneous identification of the domain of validity of a
physical theory will automatically create all kinds of mysteries and unsolvable problems - and this is
exactly what happens. Above, we have identified one of the (more subtle) problems of this kind,
concerning the role of potentials in QT, but many more could be found. Generalizing the above
argumentation concerning potentials, we claim that characteristic features of QT cannot be identified by
comparison with classical mechanics. Instead, quantum theory should be compared with its classical
limit, which is in the present
, discussed in section 10, is very important for
the proper interpretation of QT. The erronous belief (wish) that this limit can (must) be identified with classical
mechanics is closely related to the erroneous belief that QT is able to describe the dynamics of individual
particles. In this respect QT is obviously an incomplete theory, as has been pointed out many times before,
during the last eighty years, see e.g. [15], [43] , [6], [25]. Unfortunately, this erroneous opinion is historically
grown and firmly established in our thinking as shown by the ubiquitous use of phrases like ’the wave
function of the electron’. But it is clear that an erroneous identification of the domain of validity of a
physical theory will automatically create all kinds of mysteries and unsolvable problems - and this is
exactly what happens. Above, we have identified one of the (more subtle) problems of this kind,
concerning the role of potentials in QT, but many more could be found. Generalizing the above
argumentation concerning potentials, we claim that characteristic features of QT cannot be identified by
comparison with classical mechanics. Instead, quantum theory should be compared with its classical
limit, which is in the present 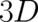 -case given by (118), (119) - we note in this context that
several ’typical’ quantum phenomena have been explained by [30] in terms of classical probability
theory. One has to compare the solutions of the classical, nonlinear equations (118), (119) with
those of the quantum mechanical, linear equations, (50), (51), in order to find out which ’typical
quantum-mechanical features’ are already given by statistical (nonlocal) correlations of the classical limit
theory and which features are really quantum-theoretical in nature - related to the nonzero value of
-case given by (118), (119) - we note in this context that
several ’typical’ quantum phenomena have been explained by [30] in terms of classical probability
theory. One has to compare the solutions of the classical, nonlinear equations (118), (119) with
those of the quantum mechanical, linear equations, (50), (51), in order to find out which ’typical
quantum-mechanical features’ are already given by statistical (nonlocal) correlations of the classical limit
theory and which features are really quantum-theoretical in nature - related to the nonzero value of
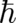 .
.