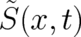 in the present theory. We assume that
in the present theory. We assume that 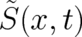 may be written as a sum of a single-valued part
may be written as a sum of a single-valued part
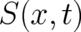 and a multi-valued part
and a multi-valued part  . Then, given that (5) holds, the derivatives of
. Then, given that (5) holds, the derivatives of 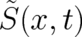 may
be written in the form
may
be written in the form
In this section we study the consequences of the multi-valuedness [[42], [70], [13]] of the quantity 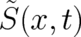 in the present theory. We assume that
in the present theory. We assume that 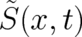 may be written as a sum of a single-valued part
may be written as a sum of a single-valued part
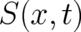 and a multi-valued part
and a multi-valued part 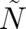 . Then, given that (5) holds, the derivatives of
. Then, given that (5) holds, the derivatives of 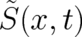 may
be written in the form
may
be written in the form
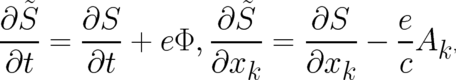 | (16) |
where the four functions 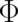 and
and 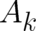 are proportional to the derivatives of
are proportional to the derivatives of 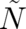 with respect to
with respect to 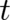 and
and
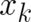 respectively (Note the change in sign of
respectively (Note the change in sign of 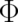 and
and 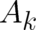 in comparison to [32]; this is
due to the fact that the multi-valued phase is now denoted by
in comparison to [32]; this is
due to the fact that the multi-valued phase is now denoted by 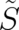 ). The physical motivations for
introducing the pre-factors
). The physical motivations for
introducing the pre-factors 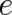 and
and  in Eq. (16) have been extensively discussed elsewhere, see
[28], [32], in an electrodynamical context. In agreement with Eq. (16),
in Eq. (16) have been extensively discussed elsewhere, see
[28], [32], in an electrodynamical context. In agreement with Eq. (16), 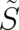 may be written in the form
[[28], [32]]
may be written in the form
[[28], [32]]
![∫
e x,t [ ]
˜ -- ′ ′ ′ ′ ′ ′
S (x, t; C ) = S (x, t )- dx kAk (x , t ) - cdt ϕ (x , t ) ,
c x0,t0;C](stader98x.png) | (17) |
as a path-integral performed along an arbitrary path 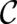 in four-dimensional space; the multi-valuedness of
in four-dimensional space; the multi-valuedness of
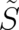 simply means that it depends not only on
simply means that it depends not only on 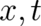 but also on the path
but also on the path 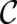 connecting the points
connecting the points
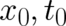 and
and 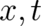 .
.
The quantity 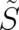 cannot be a physical observable because of its multi-valuedness. The fundamental physical
quantities to be determined by our (future) theory are the four derivatives of
cannot be a physical observable because of its multi-valuedness. The fundamental physical
quantities to be determined by our (future) theory are the four derivatives of 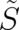 which will be rewritten here
as two observable fields
which will be rewritten here
as two observable fields 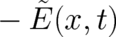 ,
, 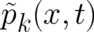 ,
,
We encounter a somewhat unusual situation in Eqs. (18), (19): On the one hand the left hand
sides are observables of our theory, on the other hand we cannot solve our (future) differential
equations for these quantities because of the peculiar multi-valued structure of 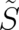 . We have to use
instead the decompositions as given by the right hand sides of (18) and (19). The latter eight
terms (the four derivatives of
. We have to use
instead the decompositions as given by the right hand sides of (18) and (19). The latter eight
terms (the four derivatives of 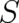 and the four scalar functions
and the four scalar functions 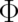 and
and 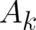 ) are single-valued
(in the mathematical sense) but need not be unique because only the left hand sides are uniquely
determined by the physical situation. We tentatively assume that the fields
) are single-valued
(in the mathematical sense) but need not be unique because only the left hand sides are uniquely
determined by the physical situation. We tentatively assume that the fields 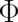 and
and 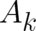 are ’given’
quantities in the sense that they represent an external influence (of ’external forces’) on the considered
statistical situation. An actual calculation has to be performed in such a way that fixed fields
are ’given’
quantities in the sense that they represent an external influence (of ’external forces’) on the considered
statistical situation. An actual calculation has to be performed in such a way that fixed fields  and
and
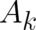 are chosen and then the differential equations are solved for
are chosen and then the differential equations are solved for 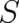 (and
(and 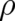 ). However,
as mentioned already, what is actually uniquely determined by the physical situation is the sum
of the two terms on the right hand sides of (18) and (19). Consequently, a different set of fixed
fields
). However,
as mentioned already, what is actually uniquely determined by the physical situation is the sum
of the two terms on the right hand sides of (18) and (19). Consequently, a different set of fixed
fields 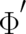 and
and 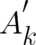 may lead to a physically equivalent, but mathematically different, solution
may lead to a physically equivalent, but mathematically different, solution
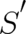 in such a way that the sum of the new terms [on the right hand sides of (18) and (19)] is the
same as the sum of the old terms. We assume here, that the formalism restores the values of the
physically relevant terms. This implies that the relation between the old and new terms is given by
in such a way that the sum of the new terms [on the right hand sides of (18) and (19)] is the
same as the sum of the old terms. We assume here, that the formalism restores the values of the
physically relevant terms. This implies that the relation between the old and new terms is given by
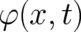 is an arbitrary, single-valued function of
is an arbitrary, single-valued function of 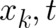 . Consequently, all ’theories’ (differential
equations for
. Consequently, all ’theories’ (differential
equations for 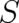 and
and 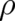 defined by the assumptions listed in section 2) should be form-invariant under the
transformations (20)-(22). These invariance transformations, predicted here from general considerations, are
(using an arbitrary function
defined by the assumptions listed in section 2) should be form-invariant under the
transformations (20)-(22). These invariance transformations, predicted here from general considerations, are
(using an arbitrary function 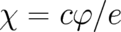 instead of
instead of 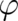 ) denoted as ’gauge transformations of the
second kind’.
) denoted as ’gauge transformations of the
second kind’.
The fields 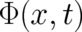 and
and 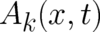 describe an external influence but their numerical value is
undefined; their value at
describe an external influence but their numerical value is
undefined; their value at 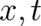 may be changed according to (21) and (22) without changing their physical
effect. Thus, these fields cannot play a local role in space and time like forces and fields in classical mechanics
and electrodynamics. What, then, is the physical meaning of these fields ? An explanation which seems obvious
in the present context is the following: They describe the statistical effect of an external influence on the
considered system (ensemble of identically prepared individual particles). The statistical effect of a force field on
an ensemble may obviously differ from the local effect of the same force field on individual particles;
thus the very existence of fields
may be changed according to (21) and (22) without changing their physical
effect. Thus, these fields cannot play a local role in space and time like forces and fields in classical mechanics
and electrodynamics. What, then, is the physical meaning of these fields ? An explanation which seems obvious
in the present context is the following: They describe the statistical effect of an external influence on the
considered system (ensemble of identically prepared individual particles). The statistical effect of a force field on
an ensemble may obviously differ from the local effect of the same force field on individual particles;
thus the very existence of fields 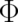 and
and 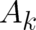 different from
different from 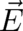 and
and 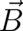 is no surprise.
The second common problem with the interpretation of the ’potentials’
is no surprise.
The second common problem with the interpretation of the ’potentials’ 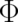 and
and 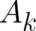 is their
non-uniqueness. It is hard to understand that a quantity ruling the behavior of individual particles
should not be uniquely defined. In contrast, this non-uniqueness is much easier to accept if
is their
non-uniqueness. It is hard to understand that a quantity ruling the behavior of individual particles
should not be uniquely defined. In contrast, this non-uniqueness is much easier to accept if 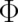 and
and
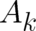 rule the behavior of ensembles instead of individual particles. We have no problem to accept
the fact that a function that represents a global (integral) effect may have many different local
realizations.
rule the behavior of ensembles instead of individual particles. We have no problem to accept
the fact that a function that represents a global (integral) effect may have many different local
realizations.
It seems that this interpretation of the potentials 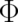 and
and 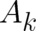 is highly relevant for the interpretation of the
effect found by [1]. If QT is interpreted as a theory about individual particles, the Aharonov-Bohm effects imply
that a charged particle may be influenced in a nonlocal way by electromagnetic fields in inaccessible regions.
This paradoxical prediction, which is however in strict agreement with QT, led even to a discussion about the
reality of these effects, see [11], [58], [31], [50]. A statistical interpretation of the potentials has apparently
never been suggested, neither in the vast literature about the Aharonov-Bohm effect nor in papers promoting the
statistical interpretation of QT; most physicists discuss this nonlocal ’paradox’ from the point of
view of ’the wave function of a single electron’. Further comments on this point may be found in
section 11.
is highly relevant for the interpretation of the
effect found by [1]. If QT is interpreted as a theory about individual particles, the Aharonov-Bohm effects imply
that a charged particle may be influenced in a nonlocal way by electromagnetic fields in inaccessible regions.
This paradoxical prediction, which is however in strict agreement with QT, led even to a discussion about the
reality of these effects, see [11], [58], [31], [50]. A statistical interpretation of the potentials has apparently
never been suggested, neither in the vast literature about the Aharonov-Bohm effect nor in papers promoting the
statistical interpretation of QT; most physicists discuss this nonlocal ’paradox’ from the point of
view of ’the wave function of a single electron’. Further comments on this point may be found in
section 11.
The expectation value 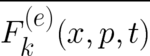 on the right hand side of (14) is to be calculated using local,
macroscopic forces whose functional form is still unknown. Both the potentials and these local forces
represent an external influence, and it is reasonable to assume that the (nonlocal) potentials are
the statistical representatives of the local forces on the r.h.s. of Eq. (14). The latter have to be
determined by the potentials but must be uniquely defined at each space-time point. The gauge-invariant
fields
on the right hand side of (14) is to be calculated using local,
macroscopic forces whose functional form is still unknown. Both the potentials and these local forces
represent an external influence, and it is reasonable to assume that the (nonlocal) potentials are
the statistical representatives of the local forces on the r.h.s. of Eq. (14). The latter have to be
determined by the potentials but must be uniquely defined at each space-time point. The gauge-invariant
fields
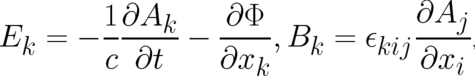 | (23) |
fulfill these requirements. As a consequence of the defining relations (23) they obey automatically the homogeneous Maxwell equations.
In a next step we rewrite the second term on the l.h.s. of Eq. (14). The commutator terms (6) take the form
![( ) ( )
1 ∂ A ∂ Φ e ∂ A ∂ A
˜ -------k-- ------- ˜ -- -----j- -----k--
S [0,k ] = - e + , S [j,k ] = - .
c ∂ t ∂ xk c ∂ xk ∂ xj](stader145x.png) | (24) |
As a consequence, they may be expressed in terms of the local fields (23), which have been introduced above for reasons of gauge-invariance. Using (24), (23) and the relation (19) for the momentum field, Eq. (14) takes the form
![⌊ ⌋
∫ ( )2
∞ ˜ ∑ ˜
3 -∂-ρ---⌈ ∂-S-- -1---- -∂-S--- ⌉
- d x + + V
- ∞ ∂ xk ∂ t 2m ∂ xj
j ,
∫ ∞ [ ] -------------------
3 e (e )
+ d x ρ --ϵ ˜viBj + eE = F (x, p, t)
c kij k k
- ∞](stader146x.png) | (25) |
with a velocity field defined by 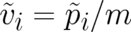 . Thus, the new terms on the l.h.s. of (25) - stemming from
the multi-valuedness of
. Thus, the new terms on the l.h.s. of (25) - stemming from
the multi-valuedness of  - take the form of an expectation value (with
- take the form of an expectation value (with  as sample space) of the
Lorentz force field
as sample space) of the
Lorentz force field
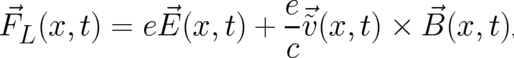 | (26) |
if the particle velocity is identified with the velocity field 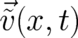 .
.
The above steps imply a relation between potentials and local fields. From the present statistical (nonlocal) point of view the potentials are more fundamental than the local fields. In contrast, considered from the point of view of macroscopic physics, the local fields are the physical quantities of primary importance and the potentials may (or may not) be introduced for mathematical convenience.