6 Spin as a statistical degree of freedom
Spin is generally believed to be a phenomenon of quantum-theoretic origin. For a long period of time,
following Dirac’s derivation of his relativistic equation, it was also believed to be essentially of
relativistic origin. This has changed since the work of [60], [41], [5], [19], [54] and others, who
showed that spin may be derived entirely in the framework of non-relativistic QT without using
any relativistic concepts. Thus, a new derivation of non-relativistic QT like the present one should
also include a derivation of the phenomenon of spin. This will be done in this and the next two
sections.
A simple idea to extend the present theory is to assume that sometimes - under certain external conditions to be
identified later - a situation occurs where the behavior of our statistical ensemble of particles cannot longer be
described by 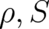 alone but requires, e.g., the double number of field variables; let us denote these by
alone but requires, e.g., the double number of field variables; let us denote these by
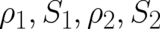 (we restrict ourselves here to spin one-half). The relations defining this
generalized theory should be formulated in such a way that the previous relations are obtained in the
appropriate limits. One could say that we undertake an attempt to introduce a new (discrete) degree of
freedom for the ensemble. If we are able to derive a non-trivial set of differential equations - with
coupling between
(we restrict ourselves here to spin one-half). The relations defining this
generalized theory should be formulated in such a way that the previous relations are obtained in the
appropriate limits. One could say that we undertake an attempt to introduce a new (discrete) degree of
freedom for the ensemble. If we are able to derive a non-trivial set of differential equations - with
coupling between 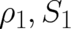 and
and 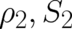 - then such a degree of freedom could exist in
nature.
- then such a degree of freedom could exist in
nature.
Using these guidelines, the basic equations of the generalized theory can be easily formulated. The probability
density and probability current take the form 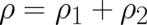 and
and 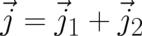 , with
, with
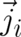 (
(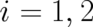 ) defined in terms of
) defined in terms of 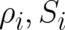 exactly as before (see section 2). Then, the continuity
equation is given by
exactly as before (see section 2). Then, the continuity
equation is given by
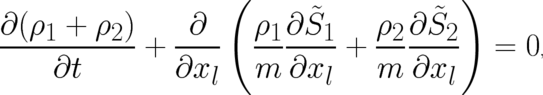 | (56) |
where we took the possibility of multi-valuedness of the “phases“ already into account, as indicated by the
notation 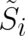 . The statistical conditions are given by the two relations
. The statistical conditions are given by the two relations
which are similar to the relations used previously (in section 2 and in I), and by an additional
equation
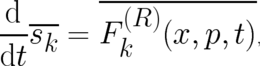 | (59) |
which is required as a consequence of our larger number of dynamic variables. Eq. (59) is best explained later; it
is written down here for completeness. The forces 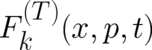 and
and 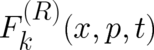 on the
r.h.s. of (58) and (59) are again subject to the “statistical constraint“, which has been defined in section 3. The
expectation values are defined as in (9)-(11).
on the
r.h.s. of (58) and (59) are again subject to the “statistical constraint“, which has been defined in section 3. The
expectation values are defined as in (9)-(11).
Performing mathematical manipulations similar to the ones reported in section 2, the l.h.s. of Eq. (58) takes the
form
![∫
˜ ˜
-d------ 3 ∂--ρ1- ∂-S1--- ∂-ρ2--∂--S2--
pk = d x [ +
dt ∂ t ∂ xk ∂ t ∂ xk
∂ ρ ∂ ˜S ∂ ρ ∂ S˜
- ----1------1- - ----2------2--+ ρ S˜ (1 ) + ρ ˜S (2 ) ],
1 [j,k ] 2 [j,k ]
∂ xk ∂ t ∂ xk ∂ t](stader277x.png) | (60) |
where the quantities ![˜ (i )
S , i = 1, 2
[j,k ]](stader278x.png) are defined as above [see Eq. (6)] but with
are defined as above [see Eq. (6)] but with 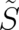 replaced by
replaced by
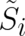 .
.
Let us write now 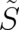 in analogy to section 2 in the form
in analogy to section 2 in the form 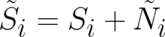 , as a sum of a
single-valued part
, as a sum of a
single-valued part 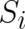 and a multi-valued part
and a multi-valued part 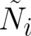 . If
. If 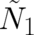 and
and 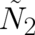 are to represent an external
influence, they must be identical and a single multi-valued part
are to represent an external
influence, they must be identical and a single multi-valued part 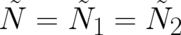 may be used
instead. The derivatives of
may be used
instead. The derivatives of 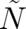 with respect to
with respect to 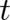 and
and 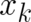 must be single-valued and we may
write
must be single-valued and we may
write
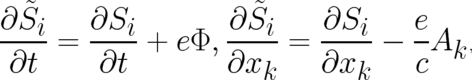 | (61) |
using the same familiar electrodynamic notation as in section 2. In this way we arrive at eight single-valued
functions to describe the external conditions and the dynamical state of our system, namely 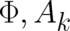 and
and
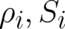 .
.
In a next step we replace 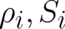 by new dynamic variables
by new dynamic variables 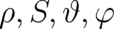 defined by
defined by
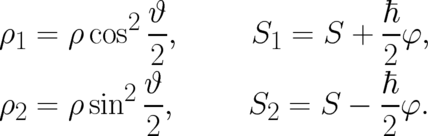 | (62) |
A transformation similar to Eq. (62) has been introduced by [65] in his reformulation of Pauli’s equation.
Obviously, the variables 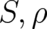 describe ’center of mass’ properties (which are common to both states
describe ’center of mass’ properties (which are common to both states 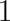 and
and
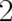 ) while
) while 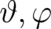 describe relative (internal) properties of the system.
describe relative (internal) properties of the system.
The dynamical variables 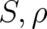 and
and 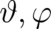 are not decoupled from each other. It turns out (see below)
that the influence of
are not decoupled from each other. It turns out (see below)
that the influence of 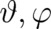 on
on 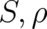 can be described in a (formally) similar way as the influence of an
external electromagnetic field if a ’vector potential’
can be described in a (formally) similar way as the influence of an
external electromagnetic field if a ’vector potential’ 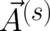 and a ’scalar potential’
and a ’scalar potential’ 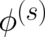 , defined
by
, defined
by
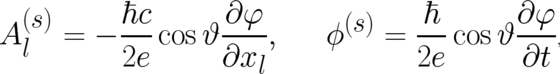 | (63) |
are introduced. Denoting these fields as ’potentials’, we should bear in mind that they are not externally
controlled but defined in terms of the internal dynamical variables. Using the abbreviations
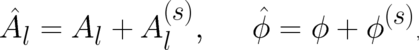 | (64) |
the second statistical condition (58) can be written in the following compact form
![∫ ∑
3 ∂ ρ ∂ S 1 ∂ S e 2
- d x -----[( ----- + e ˆϕ ) + ------ (-------- --Aˆj ) ]
∂ x ∂ t 2m ∂ x c
l j j
∫ ˆ ˆ ˆ ˆ
3 e- ∂--Al-- ∂-Aj--- e- ∂-Al--- -∂-ϕ--
+ d x ρ [ - vj ( - ) - - e ]
c ∂ xj ∂ x c ∂ t ∂ x
-------------------- ∫ l l
= F (T )(x, p, t) = d3x ρF (T )(x, p, t ),
l l](stader309x.png) | (65) |
which shows a formal similarity to the spinless case [see (14) and (24)]. The components of the velocity field
in (65) are given by
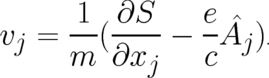 | (66) |
If now fields 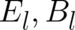 and
and 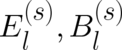 are introduced by relations analogous to (23), the second
line of (65) may be written in the form
are introduced by relations analogous to (23), the second
line of (65) may be written in the form
![∫
e e
d3x ρ [(e E⃗ + --⃗v × B⃗ ) + (e E ⃗(s) + --⃗v × B ⃗(s )) ],
l l
c c](stader313x.png) | (67) |
which shows that both types of fields, the external fields as well as the internal fields due to 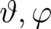 , enter the
theory in the same way, namely in the form of a Lorentz force.
, enter the
theory in the same way, namely in the form of a Lorentz force.
The first, externally controlled Lorentz force in (67) may be eliminated in exactly the same manner as in
section 3 by writing
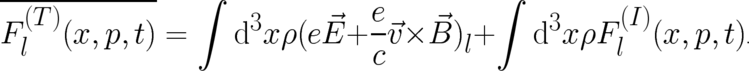 | (68) |
This means that one of the forces acting on the system as a whole is again given by a Lorentz force; there
may be other nontrivial forces  which are still to be determined. The second ’internal’
Lorentz force in (67) can, of course, not be eliminated in this way. In order to proceed, the third
statistical condition (59) must be implemented. To do that it is useful to rewrite Eq. (65) in the
form
which are still to be determined. The second ’internal’
Lorentz force in (67) can, of course, not be eliminated in this way. In order to proceed, the third
statistical condition (59) must be implemented. To do that it is useful to rewrite Eq. (65) in the
form
![∫
∂ ρ ∂ S 1 ∑ ∂ S e
3 ------ ----- ˆ ------ ------- -- ˆ 2
- d x [( + e ϕ ) + ( - Aj ) ]
∂ xl ∂ t 2m ∂ xj c
j
∫
3 ℏ-- -∂-ϑ-- ∂-φ-- -∂-φ--- ∂-φ--- ∂-ϑ-- -∂-ϑ---
+ d x ρ sin ϑ ( [ + vj ] - [ + vj ])
2 ∂ xl ∂ t ∂ xj ∂ xl ∂ t ∂ xj
------------------- ∫
(I ) (I )
= F (x, p, t) = d3x ρF (x, p, t ),
l l](stader317x.png) | (69) |
using (67), (68) and the definition (63) of the fields 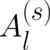 and
and 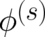 .
.
We interpret the fields 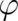 and
and 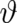 as angles (with
as angles (with 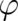 measured from the
measured from the 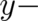 axis of our coordinate
system) determining the direction of a vector
axis of our coordinate
system) determining the direction of a vector
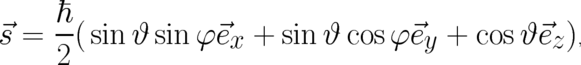 | (70) |
of constant length 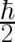 . As a consequence,
. As a consequence, 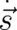 and
and 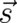 are perpendicular to each other and the classical force
are perpendicular to each other and the classical force
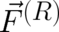 in Eq. (59) should be of the form
in Eq. (59) should be of the form  , where
, where 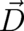 is an unknown field. In
contrast to the ’external force’, we are unable to determine the complete form of this ’internal’
force from the statistical constraint [an alternative treatment will be reported in section 8] and
set
is an unknown field. In
contrast to the ’external force’, we are unable to determine the complete form of this ’internal’
force from the statistical constraint [an alternative treatment will be reported in section 8] and
set
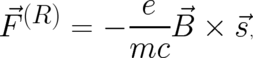 | (71) |
where 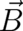 is the external ’magnetic field’, as defined by Eq. (23), and the factor in front of
is the external ’magnetic field’, as defined by Eq. (23), and the factor in front of 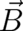 has been
chosen to yield the correct
has been
chosen to yield the correct  factor of the electron.
factor of the electron.
The differential equation
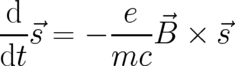 | (72) |
for particle variables 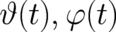 describes the rotational state of a classical magnetic dipole in a
magnetic field, see [60]. Recall that we do not require that (72) is fulfilled in the present theory. The present
variables are the fields
describes the rotational state of a classical magnetic dipole in a
magnetic field, see [60]. Recall that we do not require that (72) is fulfilled in the present theory. The present
variables are the fields 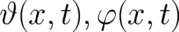 which may be thought of as describing a kind of
’rotational state’ of the statistical ensemble as a whole, and have to fulfill the ’averaged version’ (59)
of (72).
which may be thought of as describing a kind of
’rotational state’ of the statistical ensemble as a whole, and have to fulfill the ’averaged version’ (59)
of (72).
Performing steps similar to the ones described in I (see also section 2), the third statistical condition (59)
implies the following differential relations,
for the dynamic variables 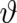 and
and 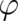 . These equations contain three fields
. These equations contain three fields 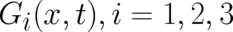 which have to obey the conditions
which have to obey the conditions
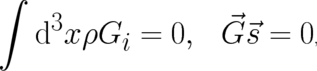 | (75) |
and are otherwise arbitrary. The ’total derivatives’ of  and
and  in (69) may now be eliminated with the
help of (73),(74) and the second line of Eq. (69) takes the form
in (69) may now be eliminated with the
help of (73),(74) and the second line of Eq. (69) takes the form
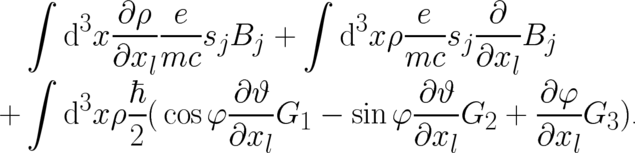 | (76) |
The second term in (76) presents an external macroscopic force. It may be eliminated from (69) by
writing
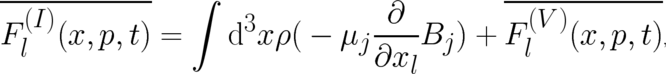 | (77) |
where the magnetic moment of the electron 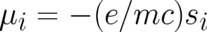 has been introduced. The
first term on the r.h.s. of (77) is the expectation value of the well-known electrodynamical force
exerted by an inhomogeneous magnetic field on the translational motion of a magnetic dipole; this
classical force plays an important role in the standard interpretation of the quantum-mechanical
Stern-Gerlach effect. It is satisfying that both translational forces, the Lorentz force as well as this dipole
force, can be derived in the present approach. The remaining unknown force
has been introduced. The
first term on the r.h.s. of (77) is the expectation value of the well-known electrodynamical force
exerted by an inhomogeneous magnetic field on the translational motion of a magnetic dipole; this
classical force plays an important role in the standard interpretation of the quantum-mechanical
Stern-Gerlach effect. It is satisfying that both translational forces, the Lorentz force as well as this dipole
force, can be derived in the present approach. The remaining unknown force 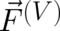 in (77)
leads (in the same way as in section 3) to a mechanical potential
in (77)
leads (in the same way as in section 3) to a mechanical potential 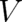 , which will be omitted for
brevity.
, which will be omitted for
brevity.
The integrand of the first term in (76) is linear in the derivative of 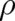 with respect to
with respect to 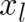 . It may
consequently be added to the first line of (69) which has the same structure. Therefore, it represents (see below)
a contribution to the generalized Hamilton-Jacobi differential equation. The third term in (76) has the
mathematical structure of a force term, but does not contain any externally controlled fields. Thus, it must also
represent a contribution to the generalized Hamilton-Jacobi equation. This implies that this third term can be
written as
. It may
consequently be added to the first line of (69) which has the same structure. Therefore, it represents (see below)
a contribution to the generalized Hamilton-Jacobi differential equation. The third term in (76) has the
mathematical structure of a force term, but does not contain any externally controlled fields. Thus, it must also
represent a contribution to the generalized Hamilton-Jacobi equation. This implies that this third term can be
written as
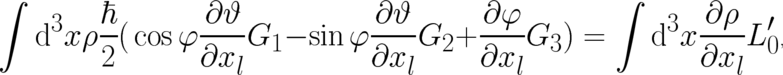 | (78) |
where 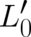 is an unknown field depending on
is an unknown field depending on 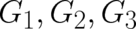 .
.
Collecting terms and restricting ourselves, as in section 5, to an isotropic law, the statistical condition (69)
takes the form of a generalized Hamilton-Jacobi equation:
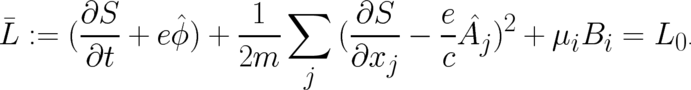 | (79) |
The unknown function 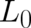 must contain
must contain 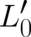 but may also contain other terms, let us write
but may also contain other terms, let us write
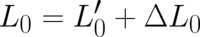 .
.
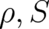 alone but requires, e.g., the double number of field variables; let us denote these by
alone but requires, e.g., the double number of field variables; let us denote these by
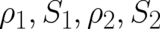 (we restrict ourselves here to spin one-half). The relations defining this
generalized theory should be formulated in such a way that the previous relations are obtained in the
appropriate limits. One could say that we undertake an attempt to introduce a new (discrete) degree of
freedom for the ensemble. If we are able to derive a non-trivial set of differential equations - with
coupling between
(we restrict ourselves here to spin one-half). The relations defining this
generalized theory should be formulated in such a way that the previous relations are obtained in the
appropriate limits. One could say that we undertake an attempt to introduce a new (discrete) degree of
freedom for the ensemble. If we are able to derive a non-trivial set of differential equations - with
coupling between 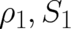 and
and 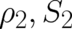 - then such a degree of freedom could exist in
nature.
- then such a degree of freedom could exist in
nature.
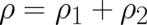 and
and 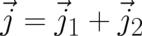 , with
, with
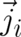 (
( ) defined in terms of
) defined in terms of 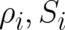 exactly as before (see section
exactly as before (see section 
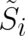 . The statistical conditions are given by the two relations
. The statistical conditions are given by the two relations 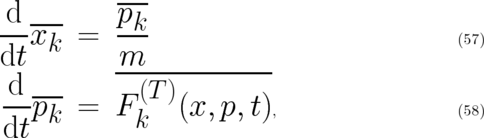
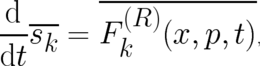
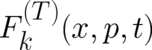 and
and 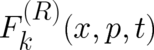 on the
r.h.s. of (
on the
r.h.s. of (![∫
˜ ˜
-d------ 3 ∂--ρ1- ∂-S1--- ∂-ρ2--∂--S2--
pk = d x [ +
dt ∂ t ∂ xk ∂ t ∂ xk
∂ ρ ∂ ˜S ∂ ρ ∂ S˜
- ----1------1- - ----2------2--+ ρ S˜ (1 ) + ρ ˜S (2 ) ],
1 [j,k ] 2 [j,k ]
∂ xk ∂ t ∂ xk ∂ t](stader277x.png)
![˜ (i )
S , i = 1, 2
[j,k ]](stader278x.png) are defined as above [see Eq. (
are defined as above [see Eq. (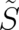 replaced by
replaced by
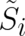 .
.
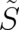 in analogy to section
in analogy to section 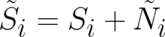 , as a sum of a
single-valued part
, as a sum of a
single-valued part 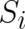 and a multi-valued part
and a multi-valued part 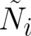 . If
. If 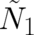 and
and 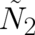 are to represent an external
influence, they must be identical and a single multi-valued part
are to represent an external
influence, they must be identical and a single multi-valued part 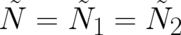 may be used
instead. The derivatives of
may be used
instead. The derivatives of 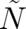 with respect to
with respect to 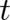 and
and 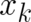 must be single-valued and we may
write
must be single-valued and we may
write
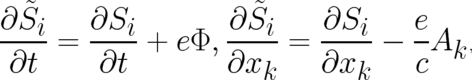
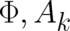 and
and
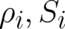 .
.
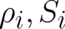 by new dynamic variables
by new dynamic variables 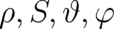 defined by
defined by
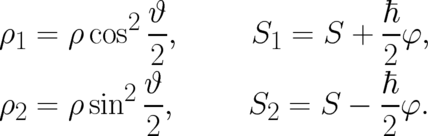
 describe ’center of mass’ properties (which are common to both states
describe ’center of mass’ properties (which are common to both states  and
and
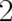 ) while
) while 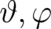 describe relative (internal) properties of the system.
describe relative (internal) properties of the system.
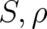 and
and 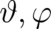 are not decoupled from each other. It turns out (see below)
that the influence of
are not decoupled from each other. It turns out (see below)
that the influence of 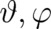 on
on 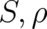 can be described in a (formally) similar way as the influence of an
external electromagnetic field if a ’vector potential’
can be described in a (formally) similar way as the influence of an
external electromagnetic field if a ’vector potential’ 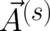 and a ’scalar potential’
and a ’scalar potential’ 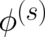 , defined
by
, defined
by
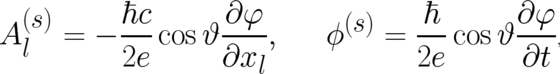
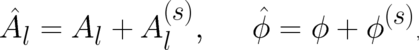
![∫ ∑
3 ∂ ρ ∂ S 1 ∂ S e 2
- d x -----[( ----- + e ˆϕ ) + ------ (-------- --Aˆj ) ]
∂ x ∂ t 2m ∂ x c
l j j
∫ ˆ ˆ ˆ ˆ
3 e- ∂--Al-- ∂-Aj--- e- ∂-Al--- -∂-ϕ--
+ d x ρ [ - vj ( - ) - - e ]
c ∂ xj ∂ x c ∂ t ∂ x
-------------------- ∫ l l
= F (T )(x, p, t) = d3x ρF (T )(x, p, t ),
l l](stader309x.png)
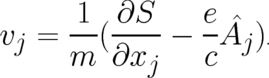
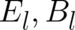 and
and 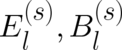 are introduced by relations analogous to (
are introduced by relations analogous to (![∫
e e
d3x ρ [(e E⃗ + --⃗v × B⃗ ) + (e E ⃗(s) + --⃗v × B ⃗(s )) ],
l l
c c](stader313x.png)
 , enter the
theory in the same way, namely in the form of a Lorentz force.
, enter the
theory in the same way, namely in the form of a Lorentz force.
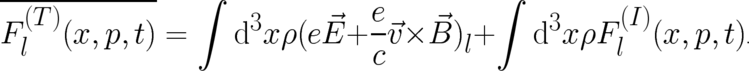
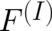 which are still to be determined. The second ’internal’
Lorentz force in (
which are still to be determined. The second ’internal’
Lorentz force in (![∫
∂ ρ ∂ S 1 ∑ ∂ S e
3 ------ ----- ˆ ------ ------- -- ˆ 2
- d x [( + e ϕ ) + ( - Aj ) ]
∂ xl ∂ t 2m ∂ xj c
j
∫
3 ℏ-- -∂-ϑ-- ∂-φ-- -∂-φ--- ∂-φ--- ∂-ϑ-- -∂-ϑ---
+ d x ρ sin ϑ ( [ + vj ] - [ + vj ])
2 ∂ xl ∂ t ∂ xj ∂ xl ∂ t ∂ xj
------------------- ∫
(I ) (I )
= F (x, p, t) = d3x ρF (x, p, t ),
l l](stader317x.png)
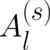 and
and 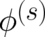 .
.
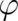 and
and 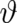 as angles (with
as angles (with 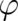 measured from the
measured from the 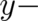 axis of our coordinate
system) determining the direction of a vector
axis of our coordinate
system) determining the direction of a vector
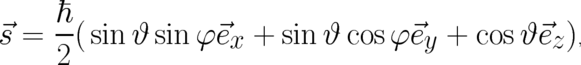
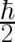 . As a consequence,
. As a consequence, 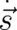 and
and 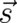 are perpendicular to each other and the classical force
are perpendicular to each other and the classical force
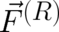 in Eq. (
in Eq. ( , where
, where 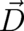 is an unknown field. In
contrast to the ’external force’, we are unable to determine the complete form of this ’internal’
force from the statistical constraint [an alternative treatment will be reported in section
is an unknown field. In
contrast to the ’external force’, we are unable to determine the complete form of this ’internal’
force from the statistical constraint [an alternative treatment will be reported in section 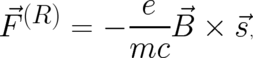
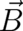 is the external ’magnetic field’, as defined by Eq. (
is the external ’magnetic field’, as defined by Eq. (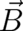 has been
chosen to yield the correct
has been
chosen to yield the correct 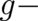 factor of the electron.
factor of the electron.
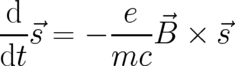
 describes the rotational state of a classical magnetic dipole in a
magnetic field, see
describes the rotational state of a classical magnetic dipole in a
magnetic field, see  which may be thought of as describing a kind of
’rotational state’ of the statistical ensemble as a whole, and have to fulfill the ’averaged version’ (
which may be thought of as describing a kind of
’rotational state’ of the statistical ensemble as a whole, and have to fulfill the ’averaged version’ (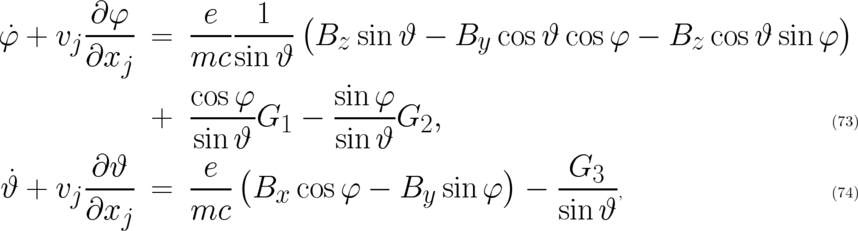
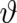 and
and 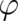 . These equations contain three fields
. These equations contain three fields 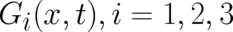 which have to obey the conditions
which have to obey the conditions
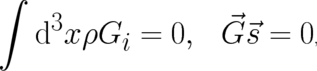
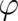 and
and 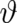 in (
in (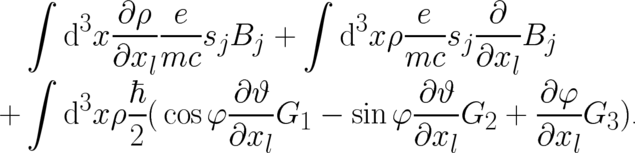
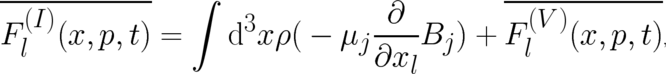
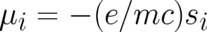 has been introduced. The
first term on the r.h.s. of (
has been introduced. The
first term on the r.h.s. of ( in (
in ( , which will be omitted for
brevity.
, which will be omitted for
brevity.
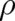 with respect to
with respect to 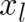 . It may
consequently be added to the first line of (
. It may
consequently be added to the first line of (
 is an unknown field depending on
is an unknown field depending on 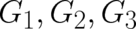 .
.
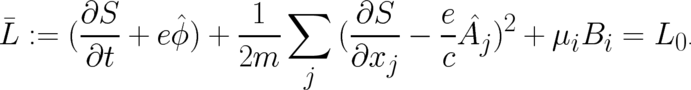
 must contain
must contain 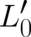 but may also contain other terms, let us write
but may also contain other terms, let us write
 .
.