[1]   O. Alter and Y. Yamamoto. Quantum Measurement of a Single System. Wiley, New York, 2001.

[2]   L. E. Ballentine. The statistical interpretation of quantum mechanics. Reviews of Modern Physics, 42:358–381, 1970.

[3]   J. A. Barrett. The Quantum Mechanics of Minds and Worlds. Oxford University Press, Oxford, 1999.

[4]   A. O. Barut. Combining Relativity and Quantum Mechanics: Schrödinger’s Interpretation of 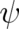. Foundations of Physics, 18:95–105, 1988.

[5]   Arieh Ben-Naim. Statistical Thermodynamics Based on Information. World Scientific Publishing, Singapore, 2008.

[6]   A. Caticha. Relative entropy and inductive inference. In G. Erickson and Y. Zhai, editors, Bayesian Inference and Maximum Entropy Methods in Science and Engineering, AIP Conference Proceedings vol. 707, page 75, 2004. See also http://www.arXiv.org e-Print archive, E-print No. physics/0311093v1.

[7]   A. C. de la Torre. On randomness in quantum mechanics. Eur. J. Phys., 29:567–575, 2008.

[8]   T. E. Faber. Fluid Dynamics for Physicists. Cambridge University Press, Cambridge, 1995.

[9]   R. A. Fisher. Statistical Methods and Scientific Inference. Oliver and Boyd, Edinburgh, 1956.

[10]   B. Roy Frieden. Fisher information as the basis for the Schrödinger wave equation. Am. J. Phys., 57(11):1004–1008, 1989.

[11]   B. Roy Frieden. Science from Fisher Information, a Unification. Cambridge University Press, Cambridge, 2004.

[12]   B. Roy Frieden and B. Soffer. Lagrangians of physics and the game of Fisher-information transfer. Phys. Rev. E, 52:2274, 1995.

[13]   M. Giaquinta and S. Hildebrandt. Calculus of Variations I. Springer, Berlin, 2004.

[14]   M. J. Hall and M. Reginatto. Quantum mechanics from a Heisenberg-type equality. Fortschr. Phys., 50:5–7, 2002.

[15]   M. J. Hall and M. Reginatto. Schrödinger equation from an exact uncertainty principle. J. Phys. A, 35:3289–3303, 2002.

[16]   Michael J. Hall. Quantum properties of classical Fisher information. Phys. Rev. A, 62:012107–1–012107–6, 2000.

[17]   D. Home and M. A. B. Whitaker. Ensemble interpretations of quantum mechanics. a modern perspective. Physics Reports, 210(4):223–317, May 1992.

[18]   E. T. Jaynes. Probability Theory: The Logic of Science. Cambridge University Press, London, 2003. p. 375.

[19]   T. F. Jordan. Why 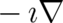is the momentum. Am. J. Phys., 43:1089, 1975.

[20]   T. F. Jordan. How relativity determines the hamiltonian description of an object in classical mechanics. Phys. Lett., A 310:123–130, 2003.

[21]   G. Kaniadakis. Statistical origin of quantum mechanics. Physica A, 307(1):172–184, 2002.

[22]   A. V. Khinchin. Mathematical Foundations of Information Theory. Dover, New York, 1957.

[23]   A. Khrennikov. Interference of probabilities and number field structure of quantum models. Ann. Phys. (Leipzig), 12(10):575–585, 2003.

[24]   U. Klein. to be published.

[25]   U. Klein. Lecture notes on superconductivity. unpublished.

[26]   U. Klein. Schrödinger’s equation with gauge coupling derived from a continuity equation. Foundations of physics, 39:964, 2009.

[27]   A. Kovner and B. Rosenstein. On quantisation ambiguity. J. Phys. A, pages 2709–2719, 1987.

[28]   S. Kullback. Information Theory and Statistics. Wiley, New-York, 1959.

[29]   Y. C. Lee and W. Zhu. The principle of minimal quantum fluctuations for the time-dependent Schrödinger equation. J. Phys. A, 32:3127–3131, 1999.

[30]   A. Messiah. Quantum Mechanics, volume I. North-Holland, Amsterdam, 1961.

[31]   L. Motz. Quantization and the classical Hamilton-Jacobi equation. Phys. Rev., 126:378–382, 1962.

[32]   J. E. Moyal. Quantum mechanics as a statistical theory. Proc. Cambridge Phil. Soc., 45:99, 1949.

[33]   E. Nelson. Quantum Fluctuations. Princeton University Press, Princeton, 1985. page 65.

[34]   H. Nikolic. Classical mechanics without determinism. Found. Phys. Lett., 19:553–566, 2006.

[35]   Asher Peres. Quantum Theory : Concepts and Methods (Fundamental Theories of Physics, Vol 57). Kluwer Academic Publishers, 1995.

[36]   M. Reginatto. Derivation of the equations of nonrelativistic quantum mechanics using the principle of minimum Fisher information. Phys. Rev. A, 58:1775–1778, 1998.

[37]   N. Rosen. The relation between classical and quantum mechanics. Am. J. Phys., 32:597–600, 1964.

[38]   R. Schiller. Quasi-classical theory of the nonspinning electron. Phys. Rev., 125(3):1100–1108, February 1962.

[39]   Erwin Schrödinger. Quantisierung als Eigenwertproblem, Erste Mitteilung. Annalen der Physik, 79:361, 1926.

[40]   D. Sen, S. K. Das, A. N. Basu, and S. Sengupta. Significance of Ehrenfest theorem in quantum-classical relationship. Current Science, 80:536–541, 2001.

[41]   C. E. Shannon and W. Weaver. The Mathematical Theory of Communication. University of Illinois Press, Urbana, Illinois, 1949.

[42]   J. R. Shewell. On the formation of quantum-mechanical operators. Am. J. Phys., 27:16–21, 1959.

[43]   T. T. Soong. Probability and Statistics for Engineers. Wiley, The Atrium, Southern Gate, Chichester, 2005.

[44]   E. C. G. Sudarshan and N. Mukunda. Classsical Dynamics: A Modern Perspective. Wiley, New York, 1974.

[45]   J. L. Synge. Classical Dynamics, in Encyclopedia of Physics: Principles of Classical Mechanics and Field theory, pages 1–223. Springer, Berlin, 1960.

[46]   J. Syska. Fisher information and quantum-classical field theory: classical statistics similarity. phys. stat. sol.(b), 244:2531–2537, 2007.

[47]   A. Tonomura, J. Endo, T. Matsuda, and T. Kawasaki. Demonstration of single-electron buildup of an interference pattern. Am. J. Phys., 57(2):117–120, 1989. see also: http://www.hqrd.hitachi.co.jp/rd/moviee/doubleslite-n.wmv.

[48]   P. Van. Unique additive information measures-Boltzmann-Gibbs-Shannon, Fisher and beyond. Physica, A 365:28–33, 2006.

[49]   Bruce van Brunt. The Calculus of Variations. Springer, New York, 2004.