12 Concluding remarks
The present derivation was based on the assumption that dynamical predictions are only possible for statistical
averages and not for single events - leaving completely open the question why predictions on single events are
impossible. This deep question remains unanswered; some speculative remarks on a possible source of the
indeterminacy have been given elsewhere [26].
Throughout this work it has been assumed that 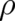 is not a (in single events) observable quantity but plays
the role of a probability density. There are of course other possibilities, besides this ’probabilistic’ (or
’immaterial’) interpretation of
is not a (in single events) observable quantity but plays
the role of a probability density. There are of course other possibilities, besides this ’probabilistic’ (or
’immaterial’) interpretation of 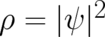 . According to the original point of view of Schrödinger and de
Broglie,
. According to the original point of view of Schrödinger and de
Broglie, 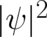 was an observable field measuring something like the density distribution of an
’extended particle’. More recently, this interpretation has been reconsidered in an interesting paper
by Barut [4]. But the results of modern high-precision measurements [47] strongly support the
probabilistic interpretation and exclude, in our opinion, the original ’material’ view of Schrödinger and de
Broglie.
was an observable field measuring something like the density distribution of an
’extended particle’. More recently, this interpretation has been reconsidered in an interesting paper
by Barut [4]. But the results of modern high-precision measurements [47] strongly support the
probabilistic interpretation and exclude, in our opinion, the original ’material’ view of Schrödinger and de
Broglie.
A third interpretation for 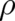 is possible. It could play the role of a density of a stream of
particles in the framework of an approximate continuum theory. This
is possible. It could play the role of a density of a stream of
particles in the framework of an approximate continuum theory. This 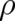 would also be an observable
quantity. An interesting problem for future research is the question if the present derivation can
be adapted in such a way that this interpretation of
would also be an observable
quantity. An interesting problem for future research is the question if the present derivation can
be adapted in such a way that this interpretation of 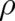 makes sense. The resulting Schrödinger
equation (32) would be a classical field equation despite the fact that it contains an adjustable parameter
makes sense. The resulting Schrödinger
equation (32) would be a classical field equation despite the fact that it contains an adjustable parameter
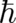 . However, it would be only approximately true (what is actually observed are particles and
not fields) and could, therefore, play a role as a starting point for a procedure known as second
quantization.
. However, it would be only approximately true (what is actually observed are particles and
not fields) and could, therefore, play a role as a starting point for a procedure known as second
quantization.
’Interaction between individual objects’ and the corresponding notion of force are macroscopic concepts. In
the microscopic domain, where according to the present point of view only statistical laws are valid, the concept
of force looses its meaning. In fact, in the quantum-mechanical formalism ’interaction’ is not described in terms
of forces but in terms of potentials (as is well known, this leads to a number of subtle questions concerning the
role of the vector potential in quantum mechanics). The relation between these two concepts is still not
completely understood; it seems that the present statistical approach offers a new point of view to study this
problem [24].
In a previous work [26] of the present author, Schrödinger’s equation has been derived from a different set of
assumptions including the postulate that the dynamic equation of state may be formulated by
means of a complex-valued state variable 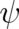 . The physical meaning of this assumption is unclear
even if it sounds plausible from a mathematical point of view. The present paper may be seen as a
continuation and completion of this previous work, insofar as this purely mathematical assumption
has been replaced now by other requirements which may be interpreted more easily in physical
terms. Finally, we mention that there are, besides the points mentioned already, several other open
problems for future research, extending the range of validity of the present approach. These include the
consideration of gauge fields [24], a generalization of the present formalism to internal degrees of
freedom (spin) and higher-dimensional configuration space (several particles), as well as a relativistic
formulation.
. The physical meaning of this assumption is unclear
even if it sounds plausible from a mathematical point of view. The present paper may be seen as a
continuation and completion of this previous work, insofar as this purely mathematical assumption
has been replaced now by other requirements which may be interpreted more easily in physical
terms. Finally, we mention that there are, besides the points mentioned already, several other open
problems for future research, extending the range of validity of the present approach. These include the
consideration of gauge fields [24], a generalization of the present formalism to internal degrees of
freedom (spin) and higher-dimensional configuration space (several particles), as well as a relativistic
formulation.
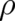 is not a (in single events) observable quantity but plays
the role of a probability density. There are of course other possibilities, besides this ’probabilistic’ (or
’immaterial’) interpretation of
is not a (in single events) observable quantity but plays
the role of a probability density. There are of course other possibilities, besides this ’probabilistic’ (or
’immaterial’) interpretation of 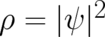 . According to the original point of view of Schrödinger and de
Broglie,
. According to the original point of view of Schrödinger and de
Broglie, 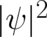 was an observable field measuring something like the density distribution of an
’extended particle’. More recently, this interpretation has been reconsidered in an interesting paper
by Barut [4]. But the results of modern high-precision measurements [47] strongly support the
probabilistic interpretation and exclude, in our opinion, the original ’material’ view of Schrödinger and de
Broglie.
was an observable field measuring something like the density distribution of an
’extended particle’. More recently, this interpretation has been reconsidered in an interesting paper
by Barut [4]. But the results of modern high-precision measurements [47] strongly support the
probabilistic interpretation and exclude, in our opinion, the original ’material’ view of Schrödinger and de
Broglie.
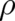 is possible. It could play the role of a density of a stream of
particles in the framework of an
is possible. It could play the role of a density of a stream of
particles in the framework of an 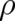 would also be an observable
quantity. An interesting problem for future research is the question if the present derivation can
be adapted in such a way that this interpretation of
would also be an observable
quantity. An interesting problem for future research is the question if the present derivation can
be adapted in such a way that this interpretation of 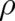 makes sense. The resulting Schrödinger
equation (
makes sense. The resulting Schrödinger
equation (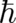 . However, it would be only approximately true (what is actually observed are particles and
not fields) and could, therefore, play a role as a starting point for a procedure known as second
quantization.
. However, it would be only approximately true (what is actually observed are particles and
not fields) and could, therefore, play a role as a starting point for a procedure known as second
quantization.
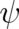 . The physical meaning of this assumption is unclear
even if it sounds plausible from a mathematical point of view. The present paper may be seen as a
continuation and completion of this previous work, insofar as this purely mathematical assumption
has been replaced now by other requirements which may be interpreted more easily in physical
terms. Finally, we mention that there are, besides the points mentioned already, several other open
problems for future research, extending the range of validity of the present approach. These include the
consideration of gauge fields
. The physical meaning of this assumption is unclear
even if it sounds plausible from a mathematical point of view. The present paper may be seen as a
continuation and completion of this previous work, insofar as this purely mathematical assumption
has been replaced now by other requirements which may be interpreted more easily in physical
terms. Finally, we mention that there are, besides the points mentioned already, several other open
problems for future research, extending the range of validity of the present approach. These include the
consideration of gauge fields