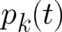 plays the role of a second dynamic variable besides the spatial
coordinate
plays the role of a second dynamic variable besides the spatial
coordinate 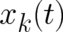 :
:
In I three different types of theories have been defined which differ from each other with regard to the role of
probability. The dogma underlying theories of type 1 is determinism with regard to single events; probability
does not play any role. If nature behaves according to this dogma, then measurements on identically prepared
individual systems yield identical results. Classical mechanics is obviously such a deterministic type 1 theory. We
shall use below (as a ’template’ for the dynamics of our statistical theories) the following version of Newton’s
law, where the particle momentum 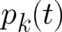 plays the role of a second dynamic variable besides the spatial
coordinate
plays the role of a second dynamic variable besides the spatial
coordinate 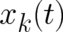 :
:
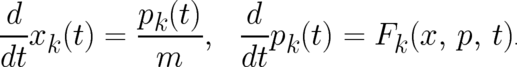 | (1) |
In classical mechanics there is no restriction as regards the admissible forces. Thus, 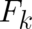 is an
arbitrary function of
is an
arbitrary function of 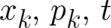 ; it is, in particular, not required that it be derivable from a
potential.
; it is, in particular, not required that it be derivable from a
potential.
Experimental data from atomic systems indicate that nature does not behave according to this single-event deterministic dogma. A simple but somewhat unfamiliar idea is, to construct a theory which is deterministic only in a statistical sense. This means that measurements on identically prepared individual systems do not yield identical results (no determinism with regard to single events) but repeated measurements on ensembles [consisting each time of a large (infinite) number of measurements on individual systems] yield identical results. In this case we have determinism with regard to ensembles (expectation values, or probabilities).
Note that such a theory is still far from chaotic even if our macroscopic anticipation of (single-event)
determinism is not satisfied. Note also that there is no reason to assume that such a statistical theory for
microscopic events is incompatible with macroscopic determinism. It is a frequently observed (but not
completely understood) phenomenon in nature that systems with many (microscopic) degrees of freedom can be
described by a much smaller number of variables. During this process of elimination of variables the
details of the corresponding microscopic theory for the individual constituents are generally lost. In
other words, there is no reason to assume that a fundamental statistical law for individual atoms
and a deterministic law for a piece of matter consisting of, say, 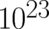 atoms should not be
compatible with each other. This way of characterizing a relation between two different physical theories
differs from the conventional reductionistic point of view but similar positions may be found in the
literature [3],[23].
atoms should not be
compatible with each other. This way of characterizing a relation between two different physical theories
differs from the conventional reductionistic point of view but similar positions may be found in the
literature [3],[23].
As discussed in I two types (referred to as type 2 and type 3) of indeterministic theories may be identified. In type 2 theories laws for individual particles exist (roughly speaking the individuality of particles remains intact) but the initial values are unknown and are described by probabilities only. An example for such a (classical-statistical) type 2 theory is statistical thermodynamics. On the other hand, in type 3 theories the amount of uncertainty is still greater, insofar as no dynamic laws for individual particles exist any more. A possible candidate for this ’extreme’ type of indeterministic theory is quantum mechanics. The method used in I to construct statistical theories is based on three assumptions listed in the last section. The first and second of these cover type 2 as well as type 3 theories, while the third - the requirement of maximal disorder - does only hold for a single type 3 theory, namely quantum mechanics. In this sense quantum mechanics may be considered as the most reasonable theory among all statistical theories defined by the first two assumptions. There is obviously an analogy between quantum mechanics and the principle of minimal Fisher information on the one hand and classical statistical mechanics and the principle of maximal entropy on the other hand; both theories are realizations of the principle of maximal disorder.
The basic equations of I (see section 3 of I) are generalized with respect to the number of spatial dimensions
and with respect to the structure of the function 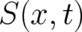 . In I
. In I 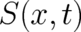 was an ’ordinary’ - i.e.
single-valued - function. Now, we allow for multi-valued functions
was an ’ordinary’ - i.e.
single-valued - function. Now, we allow for multi-valued functions 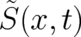 . This is possible because
. This is possible because
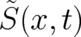 itself does not appear in any physical law (see below) of the present theory. It will be shown
that this ’degree of freedom’ is intimately related to the existence of gauge fields. A multi-valued
itself does not appear in any physical law (see below) of the present theory. It will be shown
that this ’degree of freedom’ is intimately related to the existence of gauge fields. A multi-valued
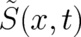 cannot be an observable quantity. However, all quantities derived from
cannot be an observable quantity. However, all quantities derived from 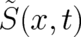 , which
occur in physical laws must be observables and must be single valued. Of particular importance
are the first derivatives with respect to
, which
occur in physical laws must be observables and must be single valued. Of particular importance
are the first derivatives with respect to 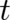 and
and 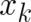 . We assume that
. We assume that 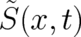 may be
written as a sum of a single-valued part
may be
written as a sum of a single-valued part 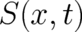 and a multi-valued part
and a multi-valued part  . Then, given
that
. Then, given
that
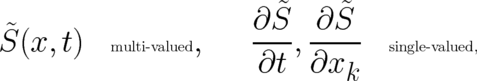 | (2) |
the derivatives of 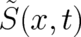 may be written in the form
may be written in the form
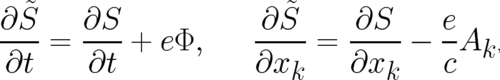 | (3) |
where the four functions 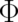 and
and 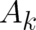 are proportional to the derivatives of the multi-valued part
are proportional to the derivatives of the multi-valued part 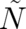 with respect to
with respect to 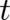 and
and 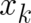 respectively (Note the change in sign of
respectively (Note the change in sign of 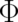 and
and 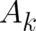 in comparison to [19];
this is due to the fact that the multi-valued phase is now denoted by
in comparison to [19];
this is due to the fact that the multi-valued phase is now denoted by 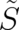 ). The physical motivations for
introducing the pre-factors
). The physical motivations for
introducing the pre-factors 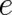 and
and  in Eq. (3) have been extensively discussed elsewhere [17],[19] in an
electrodynamical context.
in Eq. (3) have been extensively discussed elsewhere [17],[19] in an
electrodynamical context.
The necessary and sufficient condition for single-valuedness of a function 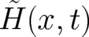 (in a subspace
(in a subspace
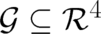 ) is that all second order derivatives of
) is that all second order derivatives of 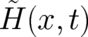 with respect to
with respect to 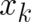 and
and 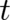 commute
with each other (in
commute
with each other (in 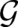 ). In this sense
). In this sense 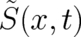 is multi-valued while the four derivatives of
is multi-valued while the four derivatives of
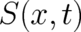 with respect to
with respect to 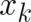 and
and 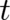 and the four functions
and the four functions 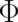 and
and 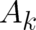 are single-valued. On the
other hand this does not mean that the latter eight quantities must be unique. Actually it will turn out that
they are not; according to the present construction only the four derivatives of
are single-valued. On the
other hand this does not mean that the latter eight quantities must be unique. Actually it will turn out that
they are not; according to the present construction only the four derivatives of 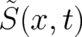 with respect to
with respect to
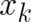 and
and 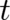 are uniquely determined by the physical situation. These derivatives define four
fields
are uniquely determined by the physical situation. These derivatives define four
fields
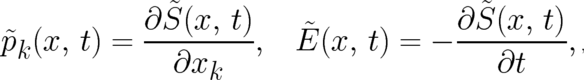 | (4) |
with dimensions of momentum and energy respectively (a quantity denoted 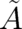 is not necessarily
multi-valued; this notation is used here to indicate that it is defined with the help of a multi-valued
is not necessarily
multi-valued; this notation is used here to indicate that it is defined with the help of a multi-valued
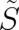 ).
).
In contrast to 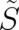 , our second fundamental dynamic variable
, our second fundamental dynamic variable 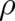 is a physical observable (in the statistical
sense) and is treated as a single-valued function. The fields
is a physical observable (in the statistical
sense) and is treated as a single-valued function. The fields 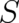 and
and 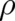 (we use the summation convention)
obey the continuity equation
(we use the summation convention)
obey the continuity equation
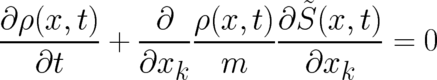 | (5) |
The statistical conditions associated with the type 1 theory (1), are obtained in the same way as in I by
replacing the observables 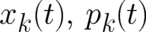 and the force field
and the force field 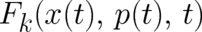 by
averages
by
averages 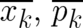 and
and 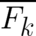 . This leads to the relations
. This leads to the relations
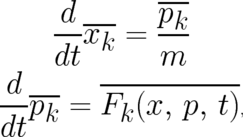 | (6) (7) |
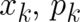 [which
should be distinguished from the observables
[which
should be distinguished from the observables 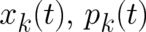 ]:
]: 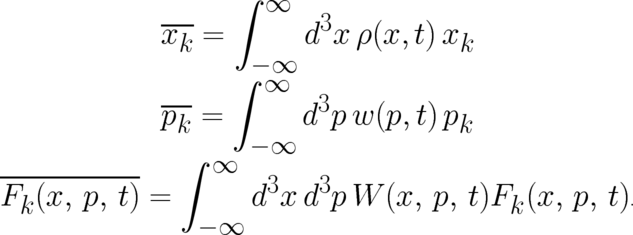 | (8) (9) (10) |
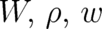 are positive semidefinite and normalized to
unity, i.e. they fulfill the conditions
are positive semidefinite and normalized to
unity, i.e. they fulfill the conditions
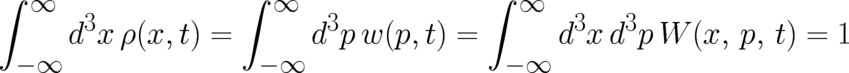 | (11) |
The densities 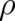 and
and 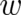 may be derived from the fundamental probability density
may be derived from the fundamental probability density 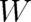 by means of the
relations
by means of the
relations
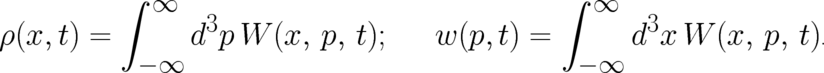 | (12) |
The present construction of the statistical conditions (6) and (7) from the type 1 theory (1) is very similar to
the treatment in I. There are, however, two differences. The first is that we allow now for a 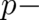 dependent
external force. This leads to a more complicated probability density
dependent
external force. This leads to a more complicated probability density 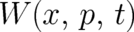 as compared to the
two decoupled densities
as compared to the
two decoupled densities 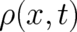 and
and 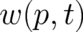 of I. The second difference, which is in fact related to
the first, is the use of a multi-valued
of I. The second difference, which is in fact related to
the first, is the use of a multi-valued 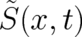 .
.