2 On probability
With regard to the role of probability, three types of physical theories may be distinguished.
- Theories of type 1 are deterministic. Single events are completely described by their known initial
values and deterministic laws (differential equations). Classical mechanics is obviously such a theory.
We include this type of theory, where probability does not play any role, in our classification scheme
because it provides a basis for the following two types of theories.
- Theories of type 2 have deterministic laws but the initial values are unknown. Therefore, no
predictions on individual events are possible, despite the fact that deterministic laws describing
individual events are valid. In order to verify a prediction of a type 2 theory a large number of
identically prepared experiments must be performed. We have no problems to understand or to
interpret such a theory because we know its just our lack of knowledge which causes the uncertainty.
An example is given by classical statistical mechanics. Of course, in order to construct a type 2
theory one needs a type 1 theory providing the deterministic laws.
- It is possible to go one step further in this direction increasing the relative importance of probability
even more. We may not only work with unknown initial values but with unknown laws as well. In
these type 3 theories there are no deterministic laws describing individual events, only probabilities
can be assigned. There is no need to mention initial values for particle trajectories any more (initial
values for probabilistic dynamical variables are still required).
Type 2 theories could also be referred to as classical (statistical) theories. Type 3 theories are most interesting
because we recognize here characteristic features of quantum mechanics. In what follows we shall try to make
this last statement more definite.
Comparing type 2 and type 3 theories, one finds two remarkable aspects. The first is a subtle kind of
“inconsistency” of type 2 theories: If we are unable to know the initial values of our observables (at a particular
time), why should we be able to know these values during the following time interval (given we know them at a
fixed time). In other words, in type 2 theories the two factors determining the final outcome of a
theoretical prediction - namely initial values and laws - are not placed on the same (realistic) footing.
This hybrid situation has been recognized before; the term ’crypto-deterministic’ has been used by
Moyal [32] to characterize classical statistical mechanics (note that the same term is also used in a very
different sense to characterize hidden variable theories [35]). Type 3 theories do not show this kind of
inconsistency.
The second observation is simply that type 2 and type 3 theories have a number of important properties in
common. Both are unable to predict the outcome of single events with certainty; only probabilities are provided
in both cases. In both theories the quantities which may be actually observed - whose time dependence may be
formulated in terms of a differential equation - are averaged observables, obtained with the help of a large
number of single experiments. These common features lead us to suspect that a general structure might exist
which comprises both types of theories.
Such a general structure should consist of a set of (statistical) conditions, which have to be obeyed by any
statistical theory. In theories of this kind observables in the conventional sense do not exist. Their role is taken
over by random variables. Likewise, conventional physical laws - differential equations for time-dependent
observables - do not exist. They are replaced by differential equations for statistical averages. These averages of
the (former) observables become the new observables, with the time 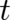 playing again the role of the
independent variable. In order to construct such general conditions one needs again (as with type 2 theories) a
deterministic (type I) theory as a “parent” theory. Given such a type 1 theory, we realize that a simple recipe to
construct a reasonable set of statistical conditions is the following: Replace all observables (of the type 1
theory) by averaged values using appropriate probability densities. In this way the dynamics of the
problem is completely transferred from the observables to the probability distributions. This program
will be carried through in the next sections, using a model system of classical mechanics as parent
theory.
playing again the role of the
independent variable. In order to construct such general conditions one needs again (as with type 2 theories) a
deterministic (type I) theory as a “parent” theory. Given such a type 1 theory, we realize that a simple recipe to
construct a reasonable set of statistical conditions is the following: Replace all observables (of the type 1
theory) by averaged values using appropriate probability densities. In this way the dynamics of the
problem is completely transferred from the observables to the probability distributions. This program
will be carried through in the next sections, using a model system of classical mechanics as parent
theory.
The above construction principle describes an unusual situation, because we are used to considering
determinism (concerning single events) as a very condition for doing science. Nevertheless, the physical
context, which is referred to is quite simple and clear, namely that nature forbids for some reason
deterministic description of single events but allows it at least “on the average”. It is certainly
true that we are not accustomed to such a kind of thinking. But to believe or not to believe in
such mechanisms of nature is basically a matter of intellectual habit. Also, the fact that quantum
mechanics is incomplete does not necessarily imply that a complete theory exists; the opposite
possibility, that no deterministic description of nature will ever be found, should also be taken into
account.
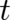 playing again the role of the
independent variable. In order to construct such general conditions one needs again (as with type 2 theories) a
deterministic (type I) theory as a “parent” theory. Given such a type 1 theory, we realize that a simple recipe to
construct a reasonable set of statistical conditions is the following: Replace all observables (of the type 1
theory) by averaged values using appropriate probability densities. In this way the dynamics of the
problem is completely transferred from the observables to the probability distributions. This program
will be carried through in the next sections, using a model system of classical mechanics as parent
theory.
playing again the role of the
independent variable. In order to construct such general conditions one needs again (as with type 2 theories) a
deterministic (type I) theory as a “parent” theory. Given such a type 1 theory, we realize that a simple recipe to
construct a reasonable set of statistical conditions is the following: Replace all observables (of the type 1
theory) by averaged values using appropriate probability densities. In this way the dynamics of the
problem is completely transferred from the observables to the probability distributions. This program
will be carried through in the next sections, using a model system of classical mechanics as parent
theory.