3 Statistical conditions
We study a simple system, a particle in an externally controlled time-independent potential 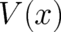 , whose
motion is restricted to a single spatial dimension (coordinate
, whose
motion is restricted to a single spatial dimension (coordinate 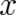 ). We use the canonical formalism of classical
mechanics to describe this system. Thus, the fundamental observables of our theory are
). We use the canonical formalism of classical
mechanics to describe this system. Thus, the fundamental observables of our theory are 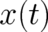 and
and 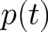 and they obey the differential equations
and they obey the differential equations
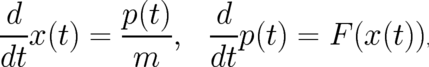 | (1) |
where 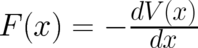 . We now create statistical conditions, associated with the
type 1 theory (1), according to the method outlined in the last section. We replace the observables
. We now create statistical conditions, associated with the
type 1 theory (1), according to the method outlined in the last section. We replace the observables
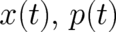 and the force field
and the force field 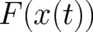 by averages
by averages 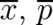 and
and 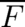 , and obtain
, and obtain
The averages in (2),(3) are mean values of the random variables 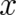 or
or 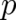 ; there is no danger of confusion
here, because the symbols
; there is no danger of confusion
here, because the symbols 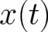 and
and 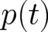 will not be used any more. In (1) only terms
occur, which depend either on the coordinate or the momentum, but not on both. Thus, to form the
averages we need two probability densities
will not be used any more. In (1) only terms
occur, which depend either on the coordinate or the momentum, but not on both. Thus, to form the
averages we need two probability densities 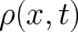 and
and 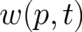 , depending on the spatial
coordinate
, depending on the spatial
coordinate 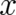 and the momentum
and the momentum 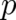 separately. Then, the averages occurring in (2),(3) are given by
Note that
separately. Then, the averages occurring in (2),(3) are given by
Note that 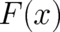 has to be replaced by
has to be replaced by 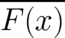 and not by
and not by 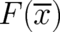 . The probability densities
. The probability densities 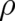 and
and 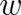 are positive semidefinite and normalized to unity. They are time-dependent because they describe the
dynamic behavior of this theory.
are positive semidefinite and normalized to unity. They are time-dependent because they describe the
dynamic behavior of this theory.
Relations (2),(3), with the definitions (4)-(6) are, to the best of my knowledge, new. They will be referred to
as “statistical conditions”. There is obviously a formal similarity of (2),(3) with Ehrenfest’s relations of quantum
mechanics, but the differential equations to be fulfilled by 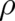 and
and 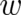 are still unknown and may well differ
from those of quantum theory. Relations (2)-(6) represent general conditions for theories which are deterministic
only with respect to statistical averages of observables and not with respect to single events. They cannot be
associated to either the classical or the quantum mechanical domain of physics. Many concrete statistical
theories (differential equations for the probability distributions) obeying these conditions may exist (see the next
section).
are still unknown and may well differ
from those of quantum theory. Relations (2)-(6) represent general conditions for theories which are deterministic
only with respect to statistical averages of observables and not with respect to single events. They cannot be
associated to either the classical or the quantum mechanical domain of physics. Many concrete statistical
theories (differential equations for the probability distributions) obeying these conditions may exist (see the next
section).
These conditions should be supplemented by a local conservation law of probability. Assuming that the
probability current is proportional to the gradient of a function 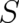 (this is the simplest possible choice and the
one realized in Hamilton-Jacobi theory, see also section 11) this conservation law is for our one-dimensional
situation given by the continuity equation
(this is the simplest possible choice and the
one realized in Hamilton-Jacobi theory, see also section 11) this conservation law is for our one-dimensional
situation given by the continuity equation
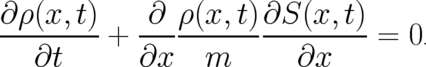 | (7) |
The derivative of 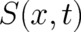 defines a field with dimension of a momentum,
defines a field with dimension of a momentum,
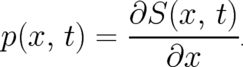 | (8) |
Eq. (8) defines a unique number 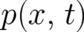 for each value of the random variable
for each value of the random variable 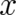 . In the next
section we will discuss the following question: Are we allowed to identify the possible values of the
random variable
. In the next
section we will discuss the following question: Are we allowed to identify the possible values of the
random variable 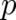 occurring in Eq. (5) with the values of the momentum field
occurring in Eq. (5) with the values of the momentum field 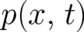 ?
?
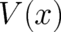 , whose
motion is restricted to a single spatial dimension (coordinate
, whose
motion is restricted to a single spatial dimension (coordinate 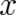 ). We use the canonical formalism of classical
mechanics to describe this system. Thus, the fundamental observables of our theory are
). We use the canonical formalism of classical
mechanics to describe this system. Thus, the fundamental observables of our theory are 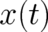 and
and 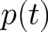 and they obey the differential equations
and they obey the differential equations
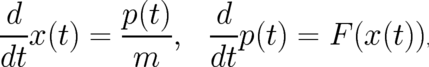
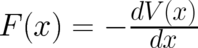 . We now create statistical conditions, associated with the
type 1 theory (
. We now create statistical conditions, associated with the
type 1 theory (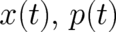 and the force field
and the force field 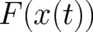 by averages
by averages 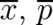 and
and 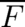 , and obtain
, and obtain
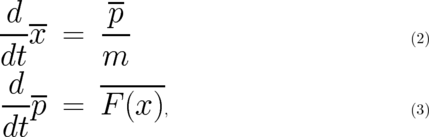
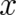 or
or 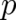 ; there is no danger of confusion
here, because the symbols
; there is no danger of confusion
here, because the symbols 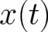 and
and 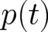 will not be used any more. In (1) only terms
occur, which depend either on the coordinate or the momentum, but not on both. Thus, to form the
averages we need two probability densities
will not be used any more. In (1) only terms
occur, which depend either on the coordinate or the momentum, but not on both. Thus, to form the
averages we need two probability densities 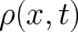 and
and 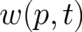 , depending on the spatial
coordinate
, depending on the spatial
coordinate 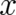 and the momentum
and the momentum 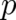 separately. Then, the averages occurring in (2),(3) are given by
separately. Then, the averages occurring in (2),(3) are given by
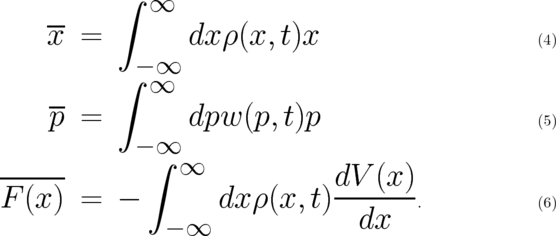
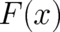 has to be replaced by
has to be replaced by 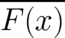 and not by
and not by 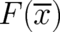 . The probability densities
. The probability densities 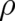 and
and 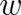 are positive semidefinite and normalized to unity. They are time-dependent because they describe the
dynamic behavior of this theory.
are positive semidefinite and normalized to unity. They are time-dependent because they describe the
dynamic behavior of this theory.
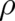 and
and 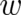 are still unknown and may well differ
from those of quantum theory. Relations (
are still unknown and may well differ
from those of quantum theory. Relations (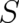 (this is the simplest possible choice and the
one realized in Hamilton-Jacobi theory, see also section
(this is the simplest possible choice and the
one realized in Hamilton-Jacobi theory, see also section 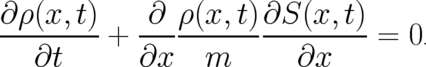
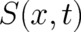 defines a field with dimension of a momentum,
defines a field with dimension of a momentum,
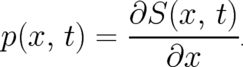
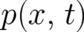 for each value of the random variable
for each value of the random variable 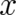 . In the next
section we will discuss the following question: Are we allowed to identify the possible values of the
random variable
. In the next
section we will discuss the following question: Are we allowed to identify the possible values of the
random variable 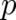 occurring in Eq. (
occurring in Eq. (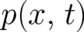 ?
?