2 Two examples for limit relations in classical physics
As our first example we consider the relation between relativistic mechanics and NM. As is well-known, in
relativistic mechanics a new fundamental constant, the speed of light  , appears, which is absent (infinitely
large) in NM. Otherwise, the mathematical structures of both theories are similar. The basic equations of
relativistic mechanics differ from (2) only by factors
, appears, which is absent (infinitely
large) in NM. Otherwise, the mathematical structures of both theories are similar. The basic equations of
relativistic mechanics differ from (2) only by factors 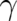 , which depend on
, which depend on 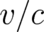 and disappear (reduce to
and disappear (reduce to
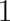 ) if
) if  becomes large,
becomes large,
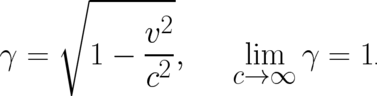 | (3) |
The relation between relativistic mechanics and NM may be summarized as follows:
- Both theories have the same mathematical structure: ordinary differential equations for trajectories.
A new fundamental constant
 appears in relativistic mechanics.
appears in relativistic mechanics.
- The limit
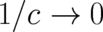 transforms the basic equations of relativistic mechanics in the basic
equations of NM; the same is true for the solutions of relativistic mechanics and NM respectively.
transforms the basic equations of relativistic mechanics in the basic
equations of NM; the same is true for the solutions of relativistic mechanics and NM respectively.
We see that relativistic mechanics and NM provide a perfect realization of a limit relation (NM
is the limit theory of relativistic mechanics) or a covering relation (relativistic mechanics is the
covering theory of NM), respectively. The significant feature is the appearance of a new fundamental
constant which allows for a transition between two different theories of the same mathematical
type. We will refer to the type of limit relation encountered in this first example as ’standard limit’
relation.
Our second example concerns the relation between NM and a probabilistic version of NM, which can be
constructed according to the following well-known recipe. We consider a phase space probability density
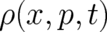 and assume that the total differential of
and assume that the total differential of 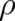 vanishes,
vanishes,
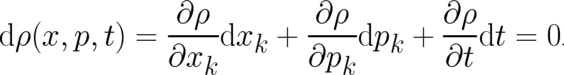 | (4) |
This means that 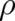 is assumed to be constant along arbitrary infinitesimal changes of
is assumed to be constant along arbitrary infinitesimal changes of 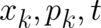 .
Next we postulate that the movement in phase space follows classical mechanics, i.e. we set
.
Next we postulate that the movement in phase space follows classical mechanics, i.e. we set
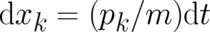 and
and 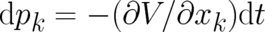 . This leads to the partial
differential equation (Liouville equation)
. This leads to the partial
differential equation (Liouville equation)
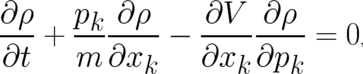 | (5) |
which has to be solved by choosing initial values 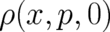 for the new dynamical variable
for the new dynamical variable
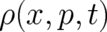 . The relation between the probabilistic version (of NM) and NM may be summarized as
follows:
. The relation between the probabilistic version (of NM) and NM may be summarized as
follows:
- The probabilistic version and NM have a different mathematical structure; the probabilistic version
is ruled by a partial differential equation, NM by an ordinary differential equation. No new constant
appears in the probabilistic version.
- The probabilistic version and NM belong to fundamentally different epistemological categories.
NM is a deterministic theory. The probabilistic version is a probabilistic (indeterministic) theory;
predictions about individual events cannot be made because the initial values for individual particles
are unknown.
The absence of a new fundamental constant prevents a simple transition between the two theories as found in
our first example. Nevertheless, a kind of limit relation can be established by means of appropriate (singular)
initial values. A probability density which is sharply peaked at 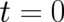 retains its shape at later times.
Inserting the Ansatz
retains its shape at later times.
Inserting the Ansatz
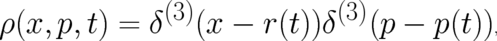 | (6) |
into Eq. (5), it is easily shown that admissible particle trajectories 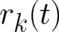 ,
, 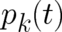 are just given by the
solutions of Newton’s equations (2). Thus, NM can be considered as a limit theory of the probabilistic version in
the sense that the manifold of solutions of a properly (with regard to singular initial values) generalized version
of the probabilistic version leads to NM. This limit relation is ’weaker’ than the one encountered in
our first example, because there is no mapping of individual solutions. By allowing for singular
solutions we have essentially constructed the union of the deterministic theory NM and the original
probabilistic version of NM; it is then no surprise that the generalized probabilistic version theory
contains NM as a special case. Considered from a formal point of view, however, the (generalized)
probabilistic version is a perfect covering theory since its manifold of solutions is larger than that of NM.
We shall refer to the kind of limit relation found in this second example as a ’deterministic’ limit
relation.
are just given by the
solutions of Newton’s equations (2). Thus, NM can be considered as a limit theory of the probabilistic version in
the sense that the manifold of solutions of a properly (with regard to singular initial values) generalized version
of the probabilistic version leads to NM. This limit relation is ’weaker’ than the one encountered in
our first example, because there is no mapping of individual solutions. By allowing for singular
solutions we have essentially constructed the union of the deterministic theory NM and the original
probabilistic version of NM; it is then no surprise that the generalized probabilistic version theory
contains NM as a special case. Considered from a formal point of view, however, the (generalized)
probabilistic version is a perfect covering theory since its manifold of solutions is larger than that of NM.
We shall refer to the kind of limit relation found in this second example as a ’deterministic’ limit
relation.
 , appears, which is absent (infinitely
large) in NM. Otherwise, the mathematical structures of both theories are similar. The basic equations of
relativistic mechanics differ from (2) only by factors
, appears, which is absent (infinitely
large) in NM. Otherwise, the mathematical structures of both theories are similar. The basic equations of
relativistic mechanics differ from (2) only by factors 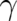 , which depend on
, which depend on 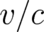 and disappear (reduce to
and disappear (reduce to
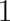 ) if
) if  becomes large,
becomes large,
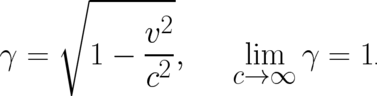
 appears in relativistic mechanics.
appears in relativistic mechanics.
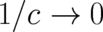 transforms the basic equations of relativistic mechanics in the basic
equations of NM; the same is true for the solutions of relativistic mechanics and NM respectively.
transforms the basic equations of relativistic mechanics in the basic
equations of NM; the same is true for the solutions of relativistic mechanics and NM respectively.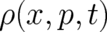 and assume that the total differential of
and assume that the total differential of 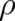 vanishes,
vanishes,
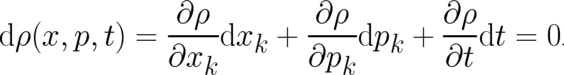
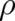 is assumed to be constant along arbitrary infinitesimal changes of
is assumed to be constant along arbitrary infinitesimal changes of 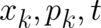 .
Next we postulate that the movement in phase space follows classical mechanics, i.e. we set
.
Next we postulate that the movement in phase space follows classical mechanics, i.e. we set
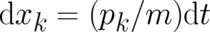 and
and 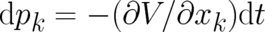 . This leads to the partial
differential equation (Liouville equation)
. This leads to the partial
differential equation (Liouville equation)
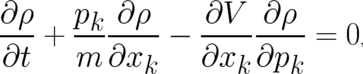
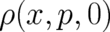 for the new dynamical variable
for the new dynamical variable
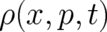 . The relation between the probabilistic version (of NM) and NM may be summarized as
follows:
. The relation between the probabilistic version (of NM) and NM may be summarized as
follows:
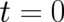 retains its shape at later times.
Inserting the Ansatz
retains its shape at later times.
Inserting the Ansatz
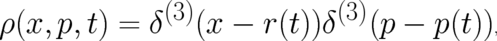
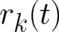 ,
, 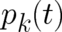 are just given by the
solutions of Newton’s equations (
are just given by the
solutions of Newton’s equations (