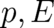 by new quantities, according to
by new quantities, according to
Both the formal transition from classical physics to quantum mechanics (quantization procedure) and the interpretation of the resulting mathematical formalism is presently dominated by the particle picture.
To begin with the interpretation, Schrödinger’s equation is used to describe, e.g., the behavior of individual electrons. At the same time the statistical nature of quantum mechanics is obvious and cannot be denied. To avoid this fundamental conflict, various complicated intellectual constructions, which I do not want to discuss here, have been - and are being- designed. But the experimental data from the micro-world (as interpreted in the particle picture) remain mysterious, no matter which one of these constructions is used.
Let us now consider the quantization process. The canonical quantization procedure consists of a set of
formal rules, which include, in particular, the replacement of classical momentum and energy observables
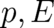 by new quantities, according to
by new quantities, according to
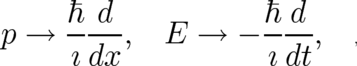 | (74) |
which then act on states of a Hilbert state, etc. By means of this well-known set of rules one obtains immediately Schrödinger’s equation (32) from the classical Hamiltonian of a single particle. While we are accustomed to ’well-established’ rules like (74), it is completely unclear why they work. It does not help if more sophisticated versions of the canonical quantization procedure are used. If for example, the structural similarity between quantum mechanical commutators and classical Poisson brackets [44] is used as a starting point, this does not at all change the mysterious nature of the jump into Hilbert space given by (74); this structural similarity is just a consequence of the fact that both theories share the same space-time (symmetries).
Thus, there seems to be no possibility to understand either the quantization procedure or the interpretation of the formalism, if a single particle picture is used as a starting point. According to a (prevailing) positivistic attitude this is no problem, since the above rules ’work’ [they illustrate perfectly von Neumann’s saying ”‘In mathematics you don’t understand things. You just get used to them”’]. On the other hand, an enormous amount of current activity is apparently aimed at an understanding of quantum mechanics.
We believe that the particle picture is inadequate, both as a starting point for the quantization process and with regard to the interpretation of the formalism. In fact, both of these aspects seem to be intimately related to each other; a comprehensible quantization procedure will lead to an adequate interpretation and a reasonable quantization procedure will only be found if the theory is interpreted in an adequate way. The position adopted here is that the most adequate way is the simplest possible way. We believe that quantum mechanics is a statistical theory whose dynamical predictions make only sense for statistical ensembles and cannot be used to describe the behavior of individual events. This ensemble interpretation of quantum mechanics (for more details the reader is referred to review articles by Ballentine [2] and by Home and Whitaker [17]) is generally accepted as the simplest possible interpretation, free from any contradictions and free from any additional assumptions expanding the range of validity of the original formalism. Fundamental conceptual problems like the “measurement problem” or the impossibility to characterize the wave function of a single particle by means of experimental data [1] do not exist in the statistical interpretation. Nevertheless it is a minority view; the reason may be that it forces us to accept that essential parts of reality are out of our control. This inconvenient conclusion can be avoided by postulating that all fundamental laws of nature must be deterministic (with regard to the description of individual events). From the point of view of this deterministic dogma, any interpretation denying the completeness of QM must be a “hidden variable theory”.
If we accept the ensemble interpretation of quantum mechanics, then the proper starting point for
quantization must be a statistical theory. The assumption of a Hilbert space for the considered system should
be avoided. This would mean postulating many essential quantum mechanical properties without
any possibility to analyze their origin. Our aim is the derivation of Schrödinger’s equation, from
which then, afterwards, the Hilbert space structure can be obtained by means of mathematical
analysis, abstraction and generalization [30]. Preferably, Schrödinger’s equation should be derived from
assumptions which can be understood in the framework of general classical (statistical as well as
deterministic) and logical concepts. This route to quantum mechanics is of course not new. Any listing of
works [39, 31, 38, 37, 10, 36, 29, 15, 14, 11, 34, 46, 26] following related ideas must necessarily be
incomplete. In the present paper an attempt has been undertaken to find a set of assumptions which is on the
one hand complete and on the other hand as simple and fundamental as possible. Throughout this work all
calculations have been performed for simplicity for a single spatial dimension. In the meantime,
after submission of this paper, the present approach has been generalized to three dimensions and
gauge fields [24]). Given that it can be further generalized to spin degrees of freedom and to a
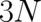 -dimensional configuration space, this would mean that essentially all of non-relativistic quantum
mechanics can be derived from the present (properly generalized) assumptions. This aim has not
yet been achieved but I will sometimes tacitly assume in the following discussion that it can be
achieved.
-dimensional configuration space, this would mean that essentially all of non-relativistic quantum
mechanics can be derived from the present (properly generalized) assumptions. This aim has not
yet been achieved but I will sometimes tacitly assume in the following discussion that it can be
achieved.
Our first, and - in a sense - central assumption was the set of relations (2), (3), which may be characterized
as a statistical version of the two fundamental equations of classical mechanics displayed in (1),
namely the definition of particle momentum and Newton’s equation. In writing down these relations
the existence of two random variables 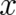 and
and 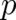 , with possible values from
, with possible values from 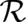 , has been
postulated. This means that appropriate experimental devices for measuring position and momentum
may be set up. The probabilities
, has been
postulated. This means that appropriate experimental devices for measuring position and momentum
may be set up. The probabilities 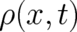 and
and 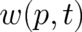 are observable quantities, to be
determined by means of a large number of individual measurements of
are observable quantities, to be
determined by means of a large number of individual measurements of 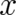 and
and 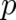 . Given such
data for
. Given such
data for 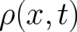 and
and 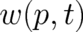 the validity of the statistical conditions (2), (3) may be
tested. Thus, these relations have a clear operational meaning. On the other hand, they do not
provide a statistical law of nature, i.e. dynamical equations for the probabilities
the validity of the statistical conditions (2), (3) may be
tested. Thus, these relations have a clear operational meaning. On the other hand, they do not
provide a statistical law of nature, i.e. dynamical equations for the probabilities 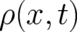 and
and
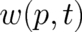 . Further constraints are required to define such laws. As shown in section 5 the statistical
framework provided by (2),(3) is very general; it contains quantum mechanics and its classical limit as
well as an infinite number of other theories. Thus, it provides a ”‘bird’s eye view”’ on quantum
theory.
. Further constraints are required to define such laws. As shown in section 5 the statistical
framework provided by (2),(3) is very general; it contains quantum mechanics and its classical limit as
well as an infinite number of other theories. Thus, it provides a ”‘bird’s eye view”’ on quantum
theory.
Our second postulate was the validity of a continuity equation of the form (7). For the type of theory considered here the validity of a local conservation law of probability is a very weak assumption - more or less a logical necessity. The special form of the probability current postulated in (7) is suggested by Hamilton-Jacobi theory (this is of course only an issue for spatial dimensions higher than one). It means that an ensemble of particles is considered for which a wave front may be defined. A detailed study of such sets of particle trajectories, which are referred to as ”‘coherent systems”’, may be found in a review article by Synge [45]. In fluid dynamics [8] corresponding fields are called ”‘potential flow fields”’
The first two postulates led to an infinite number of statistical theories (coupled differential equations for
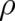 and
and 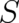 ) characterized by an unknown term
) characterized by an unknown term 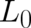 . Only the classical (limit) theory, defined by
. Only the classical (limit) theory, defined by
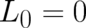 , allows for an identification of objects independent from the statistics; in this case the differential
equation for
, allows for an identification of objects independent from the statistics; in this case the differential
equation for 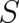 does not depend on
does not depend on 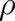 . In all other (non-classical) theories there is a
. In all other (non-classical) theories there is a 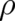 -dependent coupling
term preventing such an identification.
-dependent coupling
term preventing such an identification.
Our third postulate was the assumption that the remaining unknown function of 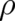 and
and 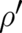 , in the
coupled differential equations for
, in the
coupled differential equations for 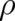 and
and 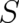 , takes a form which is in agreement with the principle of
maximal disorder (or minimal knowledge). This logical principle of simplicity is well known, in the form of a
postulate of maximal entropy, from statistical thermodynamics. In the present case it has to be implemented in a
different and more complicated way, as a postulate of minimal Fisher information. This is due to the fact that
the present equation for the determination of
, takes a form which is in agreement with the principle of
maximal disorder (or minimal knowledge). This logical principle of simplicity is well known, in the form of a
postulate of maximal entropy, from statistical thermodynamics. In the present case it has to be implemented in a
different and more complicated way, as a postulate of minimal Fisher information. This is due to the fact that
the present equation for the determination of 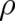 is a differential equation, i.e. it may not only depend on
is a differential equation, i.e. it may not only depend on 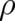 but also on derivatives of
but also on derivatives of 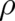 . The entropy is a functional which depends only on
. The entropy is a functional which depends only on 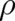 and is unable to
adjust properly with regard to this new ’degree of freedom’. Our analysis started in section 7 with a
discussion of the conventional principle of maximal entropy and led to the variational principle (58) in
section 9, which formally describes the principle of maximal disorder in the present context. Finally, in
section 10, Eq. (58) has been used to determine the unknown term, which leads to Schrödinger’s
equation.
and is unable to
adjust properly with regard to this new ’degree of freedom’. Our analysis started in section 7 with a
discussion of the conventional principle of maximal entropy and led to the variational principle (58) in
section 9, which formally describes the principle of maximal disorder in the present context. Finally, in
section 10, Eq. (58) has been used to determine the unknown term, which leads to Schrödinger’s
equation.
Schrödinger’s equation says nothing about the calculation of expectation values of 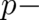 dependent
quantities. To reproduce this part of the quantum mechanical formalism, we had to implement
a further requirement, namely conservation of energy in the mean. From this fourth assumption
the standard quantum mechanical result could be recovered for terms of the form
dependent
quantities. To reproduce this part of the quantum mechanical formalism, we had to implement
a further requirement, namely conservation of energy in the mean. From this fourth assumption
the standard quantum mechanical result could be recovered for terms of the form 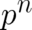 , where
, where
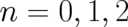 . These terms are not the only ones occurring in realistic situations. If we
want to study the behavior of charged particles in a magnetic field we should be able to calculate
expectation values of terms of the form
. These terms are not the only ones occurring in realistic situations. If we
want to study the behavior of charged particles in a magnetic field we should be able to calculate
expectation values of terms of the form 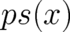 , where
, where 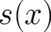 is an arbitrary function of
is an arbitrary function of
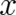 . Such terms (and more generally the inclusion of gauge fields) will be dealt with in future
work.
. Such terms (and more generally the inclusion of gauge fields) will be dealt with in future
work.
Summarizing, the most important relations of quantum mechanics have been derived from assumptions which may be characterized either as purely statistical or as statistical versions (or continuum versions) of relations of particle physics. The continuity equation and the principle of maximal disorder belong to the former class. The statistical conditions, conservation of energy in the mean, and the special form of the probability current belong to the latter class. These statistical assumptions imply quantum mechanics and are much simpler to understand than the jump into Hilbert space given by Eq. (74). Of course, all of these assumptions are relations or structural properties belonging to the quantum-mechanical formalism; it would not be possible to derive quantum mechanics from assumptions which are not quantum-mechanical in nature. However, it is not trivial that these, relatively simple and comprehensible assumptions are sufficient to derive the basic relations of the whole formalism.
As far as the interpretation of the formalism is concerned, we believe that the above derivation of the most basic equations of quantum mechanics from statistical assumptions presents a strong argument in favor of a statistical (ensemble) interpretation. This becomes even more evident, if the relation between quantum mechanics and its classical limit is considered in detail. As discussed in section 4 the transition from the classical to the quantum mechanical theory is characterized by the elimination of a deterministic element, namely the (deterministic) functional relation between position and momentum variables. Thus, quantum mechanics contains less deterministic elements (it is ’more statistical’ in nature) than its classical limit, a result in accordance with the general classification scheme set up in section 2. This loss of determinism is implicitly contained in the above assumptions and presents the essential ”‘non-classical”’ element of the present derivation.
It is interesting to compare the present derivation with other derivations of Schrödinger’s equation making use of different ”‘non-classical elements”’ [14, 29]. The loss of determinism mentioned above is also responsible for the crucial role of the concept of Fisher information in the present work. This concept was realized here in a way different from the one followed previously by Frieden and others [11, 12, 14]. On the other hand, several aspects of the present work may also be seen as a complement to this previous approach. In particular, the ’classical limit theory’ which is used as a starting point by these authors may be derived from the first two assumptions of the present work. Finally we note that there is a certain overlap of ideas between the present theory and Nelson’s stochastic mechanics [33]. In this theory it is shown that a stochastic background field combined with deterministic mechanics leads to Schrödinger’s equation. The present approach can be seen as an abstract variant of Nelson’s theory insofar as no particle trajectories and no stochastic mechanism are required but disorder is nevertheless present and plays a decisive role.