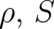 it takes the
form
it takes the
form
We study now the implications of the second statistical condition (3). Using the variables 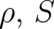 it takes the
form
it takes the
form
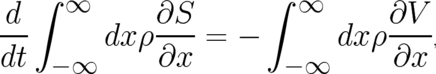 | (22) |
if 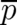 is replaced by the integral on the l.h.s. of (13). Making again use of (7), we replace in (22) the derivative
of
is replaced by the integral on the l.h.s. of (13). Making again use of (7), we replace in (22) the derivative
of 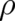 with respect to
with respect to 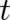 by a derivative with respect to
by a derivative with respect to 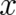 . Then, after an integration by parts, the left hand
side of (22) takes the form
. Then, after an integration by parts, the left hand
side of (22) takes the form
![∫
∞
-d-- ∂-S--
dx ρ =
dt - ∞ ∂ x
∫ [ ( ) ]
∞ 2
--1---∂-ρ-- ∂-S-- -∂---∂-S--
dx - + ρ .
- ∞ 2m ∂ x ∂ x ∂ x ∂ t](soqweb160x.png) | (23) |
Performing two more integrations by parts [a second one in (23) substituting the term with the
time-derivative of 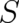 , and a third one on the right hand side of (22)], condition (3) takes the final
form
, and a third one on the right hand side of (22)], condition (3) takes the final
form
![[ ]
∫ ( )2
∞ ∂ ρ 1 ∂ S ∂ S
dx ----- ------ ----- + ----- + V = 0.
- ∞ ∂ x 2m ∂ x ∂ t](soqweb162x.png) | (24) |
Equation (24) can be considered as an integral equation for the real function 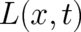 defined
by
defined
by
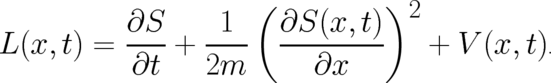 | (25) |
Obviously, (24) admits an infinite number of solutions for 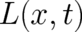 , which are given by
, which are given by
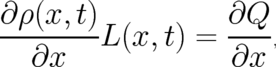 | (26) |
The function 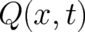 in (26) has to vanish at
in (26) has to vanish at 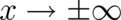 but is otherwise completely
arbitrary.
but is otherwise completely
arbitrary.
Equation (26), with fixed 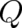 and
and 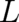 as defined by (25), is the second differential equation for our
variables
as defined by (25), is the second differential equation for our
variables 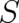 and
and 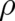 we were looking for, and defines - together with the continuity equation (7) - a
statistical theory. The dynamic behavior is completely determined by these differential equations for
we were looking for, and defines - together with the continuity equation (7) - a
statistical theory. The dynamic behavior is completely determined by these differential equations for 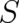 and
and
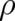 . On the other hand, the dynamic equation - in the sense of an equation describing the time-dependence of
observable quantities - is given by (2) and (3).
. On the other hand, the dynamic equation - in the sense of an equation describing the time-dependence of
observable quantities - is given by (2) and (3).
From the subset of functions 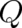 which do not depend explicitely on
which do not depend explicitely on 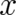 and
and 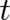 we list the following three
possibilities for
we list the following three
possibilities for 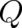 and the corresponding
and the corresponding 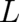 . The simplest solution is
. The simplest solution is
 | (27) |
The second 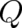 depends only on
depends only on 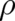 ,
,
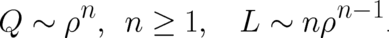 | (28) |
The third 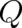 depends also on the derivative of
depends also on the derivative of 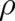 ,
,
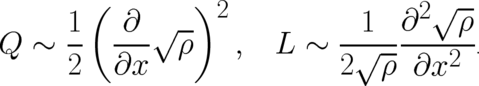 | (29) |
We discuss first (27). The statistical theory defined by (27) consists of the continuity equation (7) and [see (25)] the Hamilton-Jacobi equation,
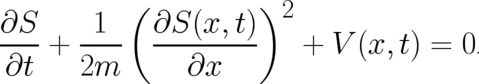 | (30) |
The fact that one of these equations agrees with the Hamilton-Jacobi equation does not imply that
this theory is a type 1 theory (making predictions about individual events). This is not the case;
many misleading statements concerning this limit may be found in the literature. It is a statistical
theory whose observables are statistical averages. However, Eq. (30) becomes a type 1 theory if it is
considered separately - and embedded in the theory of canonical transformations. The crucial point is
that (30) does not contain 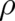 ; otherwise it could not be considered separately. This separability - or
equivalently the absence of
; otherwise it could not be considered separately. This separability - or
equivalently the absence of 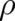 in (30) - implies that this theory is a classical (type 2) statistical
theory [37]. The function
in (30) - implies that this theory is a classical (type 2) statistical
theory [37]. The function 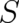 may be interpreted as describing the individual behavior of particles in the
given environment (potential
may be interpreted as describing the individual behavior of particles in the
given environment (potential 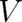 ). Loosely speaking, the function
). Loosely speaking, the function 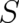 may be identified with the
considered particle; recall that
may be identified with the
considered particle; recall that 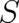 is the function generating the canonical transformation to a trivial
Hamiltonian. The identity of the particles described by
is the function generating the canonical transformation to a trivial
Hamiltonian. The identity of the particles described by 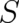 is not influenced by statistical correlations
because there is no coupling to
is not influenced by statistical correlations
because there is no coupling to 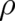 in (30). The classical theory defined by (7) and (30) may also be
formulated in terms of the variables
in (30). The classical theory defined by (7) and (30) may also be
formulated in terms of the variables 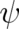 and
and 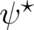 [ but not as a single equation containing
only
[ but not as a single equation containing
only 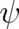 ; see the remark at the end of section (5)]. In this form it has been discussed in several
works [38, 37, 34].
; see the remark at the end of section (5)]. In this form it has been discussed in several
works [38, 37, 34].
All theories with nontrivial 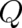 , depending on
, depending on 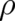 or its derivatives, should be classified as “non-classical”
(or type 3) according to the above analysis. In non-classical theories any treatment of single events (calculation
of trajectories) is impossible due to the coupling between
or its derivatives, should be classified as “non-classical”
(or type 3) according to the above analysis. In non-classical theories any treatment of single events (calculation
of trajectories) is impossible due to the coupling between 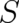 and
and 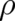 . The problem is that single events are
nevertheless real and observable. There must be a kind of dependence (correlation of non-classical type) between
these single events. But this dependence cannot be described by concepts of deterministic theories like
“interaction”.
. The problem is that single events are
nevertheless real and observable. There must be a kind of dependence (correlation of non-classical type) between
these single events. But this dependence cannot be described by concepts of deterministic theories like
“interaction”.
The impossibility to identify objects in type 3 theories - independently from the statistical context - is obviously related to the breakdown of the concept of standard random variables discussed in the last section. There, we anticipated that a standard random variable (which is defined as a unique function of another random variable) contains an element of determinism that should be absent in type 3 theories. In fact, it does not make sense to define a unique relation between measuring data - e.g. of spatial position and momentum - if the quantities to be measured cannot themselves be defined independently from statistical aspects.
The theory defined by Eq. (28) is a type 3 theory. We will not discuss it in detail because it may be shown (see the next section) to be unphysical. It has been listed here in order to have a concrete example from the large set of insignificant type 3 theories.
The theory defined by Eq. (29) is also a type 3 theory. Here, the second statistical condition takes the form
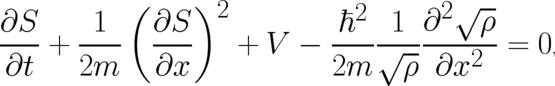 | (31) |
if the free proportionality constant in (29) is fixed according to 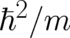 . The two equations (7) and (31)
may be rewritten in a more familiar form if the transformation (16) (with
. The two equations (7) and (31)
may be rewritten in a more familiar form if the transformation (16) (with 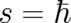 ) to variables
) to variables
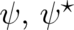 is performed. Then, both equations are contained (as real and imaginary parts) in the single
equation
is performed. Then, both equations are contained (as real and imaginary parts) in the single
equation
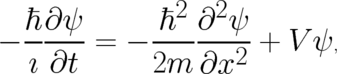 | (32) |
which is the one-dimensional version of Schrödinger’s equation [39]. Thus, quantum mechanics belongs to the class of theories defined by the above conditions. We see that the statistical conditions (2), (3) comprise both quantum mechanical and classical statistical theories; these relations express a “deep-rooted unity” [40] of the classical and quantum mechanical domain of physics.
We found an infinite number of statistical theories which are all compatible with our basic conditions and are all on equal footing so far. However, only one of them, quantum mechanics, is realized by nature. This situation leads us to ask which further conditions are required to single out quantum mechanics from this set. Knowing such condition(s) would allow us to have premises which imply quantum mechanics.
The above analysis shows that Schrödinger’s equation (32) can be derived from the condition that the
dynamic law for the probabilities takes the form of a single equation for 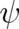 (instead of two equations for
(instead of two equations for 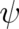 and
and 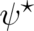 as is the case for all other theories). Our previous use of the variables
as is the case for all other theories). Our previous use of the variables 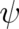 and
and 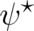 instead of
instead of
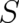 and
and 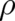 was entirely a matter of mathematical convenience. In contrast, this last condition presents a real
constraint for the physics since a different number field has been chosen [23]. Recently, Schrödingers
equation including the gauge coupling term has been derived [26] from this condition (which had to be
supplemented by two further conditions, namely the existence of a continuity equation and the
assumption of a linear time evolution law for
was entirely a matter of mathematical convenience. In contrast, this last condition presents a real
constraint for the physics since a different number field has been chosen [23]. Recently, Schrödingers
equation including the gauge coupling term has been derived [26] from this condition (which had to be
supplemented by two further conditions, namely the existence of a continuity equation and the
assumption of a linear time evolution law for 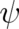 ). Of course, this is a mathematical condition
whose physical meaning is not at all clear. This formal criterion will be replaced in section 9 by a
different condition which leads to the same conclusion but may be formulated in more physical
terms.
). Of course, this is a mathematical condition
whose physical meaning is not at all clear. This formal criterion will be replaced in section 9 by a
different condition which leads to the same conclusion but may be formulated in more physical
terms.