4 On random variables
Introducing standard notions of probability theory, the fundamental sample space of the present theory is given
by all possible results of position measurements, i.e. it may be identified with the set of real numbers 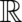 . This
set
. This
set 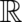 may also be identified with the possible values of a random variable “position measurement”
(whose name should strictly speaking differ from
may also be identified with the possible values of a random variable “position measurement”
(whose name should strictly speaking differ from 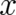 but we shall neglect such differences here). The
basic probability measure which assigns a probability to each event (subspace of
but we shall neglect such differences here). The
basic probability measure which assigns a probability to each event (subspace of 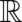 ) is given by
) is given by
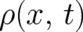 . According to standard probability theory the field
. According to standard probability theory the field 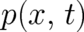 defined by (8) is itself a
random variable. We may consider it as a function of the random variable
defined by (8) is itself a
random variable. We may consider it as a function of the random variable 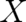 (denoting “position
measurement”) or as a random variable defined independently on the fundamental event space
(denoting “position
measurement”) or as a random variable defined independently on the fundamental event space
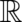 ; it makes no difference. Its probability density is uniquely determined by
; it makes no difference. Its probability density is uniquely determined by 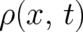 and
the function
and
the function 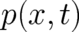 . In order to avoid confusion of names it may be useful to denote the
derivative of
. In order to avoid confusion of names it may be useful to denote the
derivative of 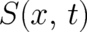 with respect to
with respect to 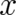 by
by 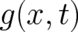 instead of
instead of 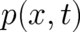 . Thus
. Thus
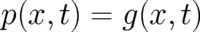 and the notation
and the notation 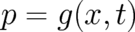 indicates that a random variable
indicates that a random variable
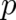 defined by the function
defined by the function 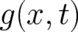 exists (the time variable will sometimes be omitted for
brevity).
exists (the time variable will sometimes be omitted for
brevity).
In order to study this important point further, we rewrite the standard result for the probability density of
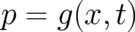 in a form more appropriate for physical considerations (a form apparently not easily
found in textbooks on probability). For the simplest possible situation, a denumerable sample space with
elements
in a form more appropriate for physical considerations (a form apparently not easily
found in textbooks on probability). For the simplest possible situation, a denumerable sample space with
elements 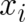 , a probability measure
, a probability measure 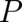 , and a invertible function
, and a invertible function 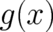 , the probability that an event
, the probability that an event
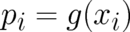 occurs is obviously given by
occurs is obviously given by 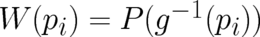 . This
result is the starting point to obtain
. This
result is the starting point to obtain 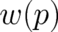 , the probability density of a continuous random
variable
, the probability density of a continuous random
variable 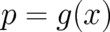 , which is defined by a non-invertible function
, which is defined by a non-invertible function 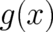 . It is given
by [43]
. It is given
by [43]
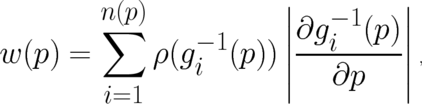 | (9) |
where 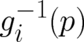 denotes the
denotes the 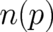 solutions (the number of solutions depends on
solutions (the number of solutions depends on 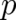 ) of the equation
) of the equation
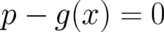 . Using a well-known formula for Dirac‘s delta function
. Using a well-known formula for Dirac‘s delta function 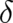 , applied
to the case where the argument of
, applied
to the case where the argument of 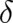 is an arbitrary function, Eq.(9) may be rewritten in the
form
is an arbitrary function, Eq.(9) may be rewritten in the
form
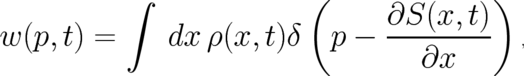 | (10) |
where we came back to our original notation, writing down the  dependencies of
dependencies of 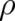 and
and 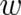 and
replacing
and
replacing 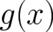 by
by 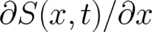 .
.
The representation (10) reveals very clearly a hybrid nature of random variables defined as (nontrivial)
functions on the event space 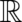 . They are partly defined by a probabilistic quantity [namely
. They are partly defined by a probabilistic quantity [namely 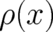 ] and
partly by a deterministic relation [namely
] and
partly by a deterministic relation [namely 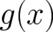 ]. The deterministic nature of the latter is expressed by the
singular (delta-function) shape of the associated probability. Such densities occur in classical statistics, i.e. in
type 2 theories; Eq. (10) may obviously be obtained by performing an integration over
]. The deterministic nature of the latter is expressed by the
singular (delta-function) shape of the associated probability. Such densities occur in classical statistics, i.e. in
type 2 theories; Eq. (10) may obviously be obtained by performing an integration over 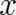 of the classical phase
space probability density
of the classical phase
space probability density 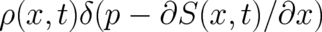 . Considered from an operational
point of view, the hybrid nature of random variables may be described as follows. Deterministic
predictions for random variables
. Considered from an operational
point of view, the hybrid nature of random variables may be described as follows. Deterministic
predictions for random variables 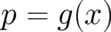 are impossible, as are deterministic predictions
for the original variables
are impossible, as are deterministic predictions
for the original variables 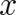 . But once a number
. But once a number 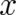 has been observed in an experiment, then
the value of
has been observed in an experiment, then
the value of 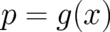 is with certainty given by the defining function
is with certainty given by the defining function 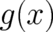 . If no
such relation exists, this does not necessarily imply that
. If no
such relation exists, this does not necessarily imply that 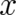 and
and 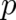 are completely independent.
Many other more complicated (’nonlocal’ or ’probabilistic’) relations between such variables are
conceivable.
are completely independent.
Many other more complicated (’nonlocal’ or ’probabilistic’) relations between such variables are
conceivable.
We formulated general conditions comprising both type 2 and type 3 theories. Thus, as far as this general
framework is concerned we can certainly not dispense with the standard notion of random variables,
which are basic ingredients of type 2 theories; such variables will certainly occur as special (type
2) cases in our formalism. But, of course, we are essentially interested in the characterization of
type 3 theories and the form of Eq. (10) shows that the standard notion of random variable is not
necessarily meaningful in a type 3 theory. Thus we will allow for the possibility of random variables
which are not defined by deterministic relations of the standard type, as functions on the sample
space.
This situation leads to a number of questions. We may, e.g. ask: Can we completely dispense with the the
standard concept of random variables if we are dealing exclusively with a type 3 theory ? The answer is certainly
no; it seems impossible to formulate a physical theory without any deterministic relations. In fact, a
deterministic relation, corresponding to a standard random variable 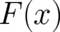 , has already been anticipated in
Eq. (6). If in a position measurement of a particle a number
, has already been anticipated in
Eq. (6). If in a position measurement of a particle a number 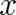 is observed, then the particle is - at the time of
the measurement - with certainty under the influence of a force
is observed, then the particle is - at the time of
the measurement - with certainty under the influence of a force 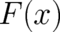 . Thus, an allowed class of
deterministic relations might contain “given” functions, describing externally controlled influences like forces
. Thus, an allowed class of
deterministic relations might contain “given” functions, describing externally controlled influences like forces
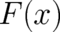 or potentials
or potentials 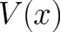 .
.
There may be other standard random variables. To decide on purely logical grounds which relations of a type
3 theory are deterministic and which are not is not an obvious matter. However, one would suspect that the
deterministic relations should be of an universal nature; e.g. they should hold both in type 2 and type 3 theories.
Further, we may expect that all relations which are a logical consequence of the structure of space-time should
belong to this class. Such a quantity is the kinetic energy. In fact, for the currently considered nonrelativistic
range of physics, the functional form of the kinetic energy can be derived from the structure of the Galilei group
both in the mathematical framework of classical mechanics [20] and quantum mechanics [19]. We refer to the
kinetic energy 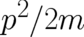 as a standard random variable insofar as it is a prescribed function of
as a standard random variable insofar as it is a prescribed function of
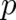 (but it is, because it is a function of
(but it is, because it is a function of 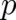 , not a standard random variable with respect to the
fundamental probability measure
, not a standard random variable with respect to the
fundamental probability measure 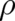 ). Combining the standard random variables “kinetic energy” and
“potential” we obtain a standard random variable “energy”, which will be studied in more detail in
section 6.
). Combining the standard random variables “kinetic energy” and
“potential” we obtain a standard random variable “energy”, which will be studied in more detail in
section 6.
Thus, in the present framework, particle momentum will, in general, not be considered as a
standard random variable. This means that an element of determinism has been eliminated from the
theoretical description. It seems that this elimination is one of the basic steps in the transition from
type 2 to type 3 theories. The functional form of the probability density 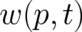 , and its
relation to
, and its
relation to 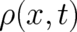 , are one of the main objectives of the present study. According to the
above discussion a measurement of position does no longer determine momentum at the time of the
measurement. However the set of all position measurements [represented formally by the probability
density
, are one of the main objectives of the present study. According to the
above discussion a measurement of position does no longer determine momentum at the time of the
measurement. However the set of all position measurements [represented formally by the probability
density 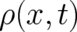 ] may still determine (in a manner still to be clarified) the set of all momentum
measurements [the probability
] may still determine (in a manner still to be clarified) the set of all momentum
measurements [the probability 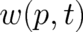 ]. Interestingly, Torre [7], using a completely different
approach, arrived at a similar conclusion, namely that the quantum mechanical ’variables’ position and
momentum cannot be random variables in the conventional sense. For simplicity we will continue to use
the term random variable for
]. Interestingly, Torre [7], using a completely different
approach, arrived at a similar conclusion, namely that the quantum mechanical ’variables’ position and
momentum cannot be random variables in the conventional sense. For simplicity we will continue to use
the term random variable for 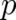 , and will add the attributes ”‘standard”’ or “nonstandard” if
required.
, and will add the attributes ”‘standard”’ or “nonstandard” if
required.
As a first step in our study of 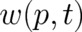 , we will now investigate the integral equation (2) and will
derive a relation for
, we will now investigate the integral equation (2) and will
derive a relation for 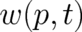 which will be used again in section 6. In the course of the following
calculations the behavior of
which will be used again in section 6. In the course of the following
calculations the behavior of 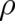 and
and 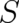 at infinity will frequently be required. We know that
at infinity will frequently be required. We know that 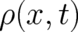 is
normalizable and vanishes at infinity. More specifically, we shall assume that
is
normalizable and vanishes at infinity. More specifically, we shall assume that 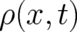 and
and 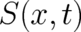 obey the following conditions:
obey the following conditions:
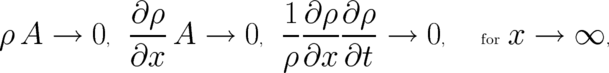 | (11) |
where 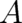 is anyone of the following factors
is anyone of the following factors
 | (12) |
Roughly speaking, condition (11) means that 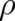 vanishes faster than
vanishes faster than 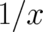 and
and 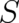 is nonsingular at
infinity. Whenever in the following an integration by parts will be performed, one of the conditions (11) will be
used to eliminate the resulting boundary term. For brevity we shall not refer to (11) any more; it will be
sufficiently clear in the context of the calculation which one of the factors in (12) will be referred
to.
is nonsingular at
infinity. Whenever in the following an integration by parts will be performed, one of the conditions (11) will be
used to eliminate the resulting boundary term. For brevity we shall not refer to (11) any more; it will be
sufficiently clear in the context of the calculation which one of the factors in (12) will be referred
to.
We look for differential equations for our fields 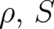 which are compatible with (2)-(7). According to
the above discussion we are not allowed to identify (8) with the random variable
which are compatible with (2)-(7). According to
the above discussion we are not allowed to identify (8) with the random variable 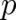 . Using (7) we replace the
derivative with respect to
. Using (7) we replace the
derivative with respect to 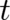 in (2) by a derivative with respect to
in (2) by a derivative with respect to 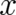 and perform an integration by parts.
Then, (2) takes the form
and perform an integration by parts.
Then, (2) takes the form
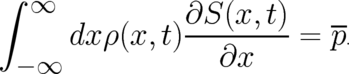 | (13) |
Eq. (13) shows that the averaged value of the random variable 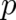 is the expectation value of the field
is the expectation value of the field
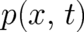 . In the next section we shall insert this expression for
. In the next section we shall insert this expression for 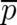 in the second statistical condition (3).
More specific results for the probability density
in the second statistical condition (3).
More specific results for the probability density 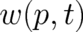 will be obtained later (in section 10). As an
intermediate step, we now use (13) and (5) to derive a relation for
will be obtained later (in section 10). As an
intermediate step, we now use (13) and (5) to derive a relation for 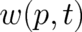 , introducing thereby an
important change of variables.
, introducing thereby an
important change of variables.
We replace the variables 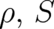 by new variables
by new variables 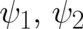 defined by
defined by
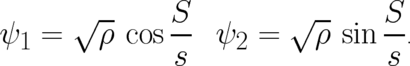 | (14) |
We may as well introduce the imaginary unit and define the complex field 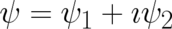 . Then,
the last transformation and its inverse may be written as
. Then,
the last transformation and its inverse may be written as
We note that so far no new condition or constraint has been introduced; choosing one of the sets of real variables
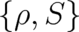 ,
, 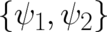 , or the set
, or the set 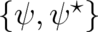 of complex fields is just a matter of
mathematical convenience. Using
of complex fields is just a matter of
mathematical convenience. Using 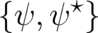 the integrand on the left hand side of (13) takes the
form
the integrand on the left hand side of (13) takes the
form
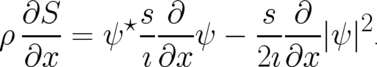 | (17) |
The derivative of 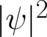 may be omitted under the integral sign and (13) takes the form
may be omitted under the integral sign and (13) takes the form
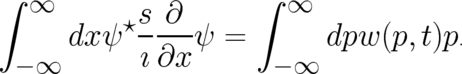 | (18) |
We introduce the Fourier transform of 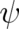 , defined by
, defined by
The constant 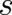 , introduced in Eq. (14), has the dimension of an action, which means that
, introduced in Eq. (14), has the dimension of an action, which means that 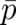 has the
dimension of a momentum. Performing the Fourier transform one finds that the momentum probability density
may be written as
has the
dimension of a momentum. Performing the Fourier transform one finds that the momentum probability density
may be written as
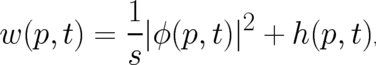 | (21) |
where the integral over 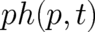 has to vanish. Using Parseval’s formula and the fact that both
has to vanish. Using Parseval’s formula and the fact that both
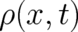 and
and 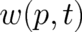 are normalized to unity we find that the integral of
are normalized to unity we find that the integral of 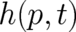 has to vanish
too.
has to vanish
too.
Using the continuity equation (7) and the first statistical condition (2) we found two results
[namely (18) and (21)] which reduce for 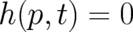 to characteristic relations of the
quantum mechanical formalism. However, the function
to characteristic relations of the
quantum mechanical formalism. However, the function 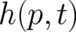 , as well as the probability
density
, as well as the probability
density 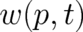 we are finally interested in, is still unknown, because the validity of the
deterministic relation (8) is not guaranteed in the present general formalism allowing for type 3
theories. In the next section the implications of the second statistical condition will be studied without
using
we are finally interested in, is still unknown, because the validity of the
deterministic relation (8) is not guaranteed in the present general formalism allowing for type 3
theories. In the next section the implications of the second statistical condition will be studied without
using 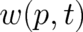 . We shall come back to the problem of the determination of
. We shall come back to the problem of the determination of 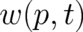 in
section 7.
in
section 7.
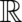 . This
set
. This
set 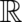 may also be identified with the possible values of a random variable “position measurement”
(whose name should strictly speaking differ from
may also be identified with the possible values of a random variable “position measurement”
(whose name should strictly speaking differ from 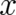 but we shall neglect such differences here). The
basic probability measure which assigns a probability to each event (subspace of
but we shall neglect such differences here). The
basic probability measure which assigns a probability to each event (subspace of 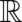 ) is given by
) is given by
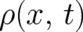 . According to standard probability theory the field
. According to standard probability theory the field 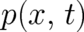 defined by (8) is itself a
random variable. We may consider it as a function of the random variable
defined by (8) is itself a
random variable. We may consider it as a function of the random variable 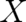 (denoting “position
measurement”) or as a random variable defined independently on the fundamental event space
(denoting “position
measurement”) or as a random variable defined independently on the fundamental event space
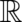 ; it makes no difference. Its probability density is uniquely determined by
; it makes no difference. Its probability density is uniquely determined by 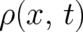 and
the function
and
the function 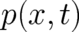 . In order to avoid confusion of names it may be useful to denote the
derivative of
. In order to avoid confusion of names it may be useful to denote the
derivative of 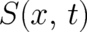 with respect to
with respect to 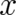 by
by 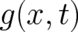 instead of
instead of 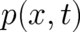 . Thus
. Thus
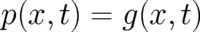 and the notation
and the notation 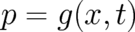 indicates that a random variable
indicates that a random variable
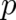 defined by the function
defined by the function 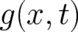 exists (the time variable will sometimes be omitted for
brevity).
exists (the time variable will sometimes be omitted for
brevity).
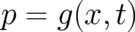 in a form more appropriate for physical considerations (a form apparently not easily
found in textbooks on probability). For the simplest possible situation, a denumerable sample space with
elements
in a form more appropriate for physical considerations (a form apparently not easily
found in textbooks on probability). For the simplest possible situation, a denumerable sample space with
elements 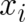 , a probability measure
, a probability measure 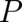 , and a invertible function
, and a invertible function 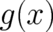 , the probability that an event
, the probability that an event
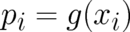 occurs is obviously given by
occurs is obviously given by 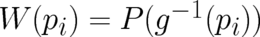 . This
result is the starting point to obtain
. This
result is the starting point to obtain 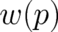 , the probability density of a continuous random
variable
, the probability density of a continuous random
variable 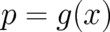 , which is defined by a non-invertible function
, which is defined by a non-invertible function 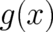 . It is given
by
. It is given
by 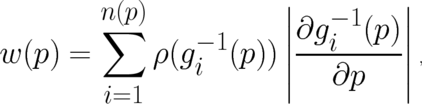
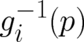 denotes the
denotes the 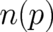 solutions (the number of solutions depends on
solutions (the number of solutions depends on 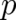 ) of the equation
) of the equation
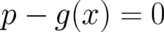 . Using a well-known formula for Dirac‘s delta function
. Using a well-known formula for Dirac‘s delta function 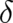 , applied
to the case where the argument of
, applied
to the case where the argument of 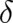 is an arbitrary function, Eq.(
is an arbitrary function, Eq.(
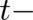 dependencies of
dependencies of 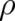 and
and 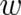 and
replacing
and
replacing 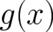 by
by 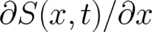 .
.
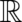 . They are partly defined by a probabilistic quantity [namely
. They are partly defined by a probabilistic quantity [namely 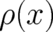 ] and
partly by a deterministic relation [namely
] and
partly by a deterministic relation [namely 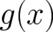 ]. The deterministic nature of the latter is expressed by the
singular (delta-function) shape of the associated probability. Such densities occur in classical statistics, i.e. in
type 2 theories; Eq. (
]. The deterministic nature of the latter is expressed by the
singular (delta-function) shape of the associated probability. Such densities occur in classical statistics, i.e. in
type 2 theories; Eq. (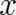 of the classical phase
space probability density
of the classical phase
space probability density 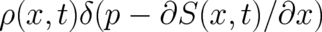 . Considered from an operational
point of view, the hybrid nature of random variables may be described as follows. Deterministic
predictions for random variables
. Considered from an operational
point of view, the hybrid nature of random variables may be described as follows. Deterministic
predictions for random variables 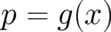 are impossible, as are deterministic predictions
for the original variables
are impossible, as are deterministic predictions
for the original variables 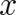 . But once a number
. But once a number 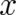 has been observed in an experiment, then
the value of
has been observed in an experiment, then
the value of 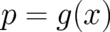 is
is 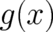 . If no
such relation exists, this does not necessarily imply that
. If no
such relation exists, this does not necessarily imply that 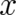 and
and 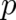 are completely independent.
Many other more complicated (’nonlocal’ or ’probabilistic’) relations between such variables are
conceivable.
are completely independent.
Many other more complicated (’nonlocal’ or ’probabilistic’) relations between such variables are
conceivable.
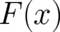 , has already been anticipated in
Eq. (
, has already been anticipated in
Eq. (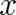 is observed, then the particle is - at the time of
the measurement -
is observed, then the particle is - at the time of
the measurement - 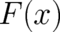 . Thus, an allowed class of
deterministic relations might contain “given” functions, describing externally controlled influences like forces
. Thus, an allowed class of
deterministic relations might contain “given” functions, describing externally controlled influences like forces
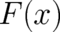 or potentials
or potentials 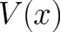 .
.
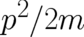 as a standard random variable insofar as it is a prescribed function of
as a standard random variable insofar as it is a prescribed function of
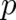 (but it is, because it is a function of
(but it is, because it is a function of 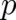 , not a standard random variable with respect to the
fundamental probability measure
, not a standard random variable with respect to the
fundamental probability measure 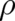 ). Combining the standard random variables “kinetic energy” and
“potential” we obtain a standard random variable “energy”, which will be studied in more detail in
section
). Combining the standard random variables “kinetic energy” and
“potential” we obtain a standard random variable “energy”, which will be studied in more detail in
section  , and its
relation to
, and its
relation to 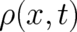 , are one of the main objectives of the present study. According to the
above discussion a measurement of position does no longer determine momentum at the time of the
measurement. However the set of all position measurements [represented formally by the probability
density
, are one of the main objectives of the present study. According to the
above discussion a measurement of position does no longer determine momentum at the time of the
measurement. However the set of all position measurements [represented formally by the probability
density 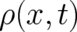 ] may still determine (in a manner still to be clarified) the set of all momentum
measurements [the probability
] may still determine (in a manner still to be clarified) the set of all momentum
measurements [the probability 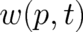 ]. Interestingly, Torre
]. Interestingly, Torre  , and will add the attributes ”‘standard”’ or “nonstandard” if
required.
, and will add the attributes ”‘standard”’ or “nonstandard” if
required.
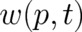 , we will now investigate the integral equation (
, we will now investigate the integral equation (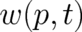 which will be used again in section
which will be used again in section 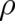 and
and 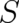 at infinity will frequently be required. We know that
at infinity will frequently be required. We know that 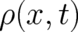 is
normalizable and vanishes at infinity. More specifically, we shall assume that
is
normalizable and vanishes at infinity. More specifically, we shall assume that 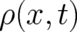 and
and 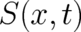 obey the following conditions:
obey the following conditions:
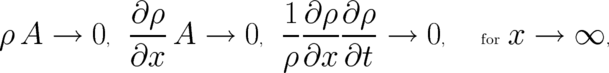
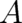 is anyone of the following factors
is anyone of the following factors
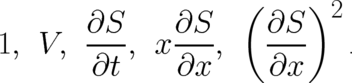
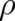 vanishes faster than
vanishes faster than 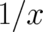 and
and 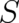 is nonsingular at
infinity. Whenever in the following an integration by parts will be performed, one of the conditions (
is nonsingular at
infinity. Whenever in the following an integration by parts will be performed, one of the conditions (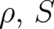 which are compatible with (
which are compatible with (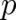 . Using (
. Using (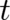 in (
in (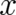 and perform an integration by parts.
Then, (
and perform an integration by parts.
Then, (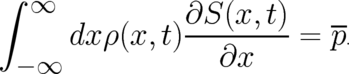
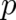 is the expectation value of the field
is the expectation value of the field
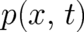 . In the next section we shall insert this expression for
. In the next section we shall insert this expression for 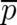 in the second statistical condition (
in the second statistical condition (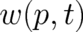 will be obtained later (in section
will be obtained later (in section 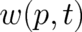 , introducing thereby an
important change of variables.
, introducing thereby an
important change of variables.
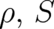 by new variables
by new variables 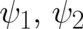 defined by
defined by
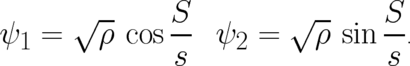
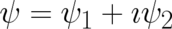 . Then,
the last transformation and its inverse may be written as
. Then,
the last transformation and its inverse may be written as 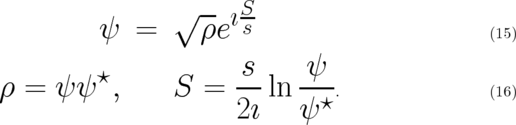
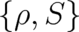 ,
, 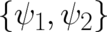 , or the set
, or the set 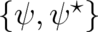 of complex fields is just a matter of
mathematical convenience. Using
of complex fields is just a matter of
mathematical convenience. Using 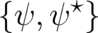 the integrand on the left hand side of (13) takes the
form
the integrand on the left hand side of (13) takes the
form
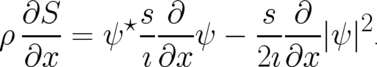
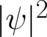 may be omitted under the integral sign and (
may be omitted under the integral sign and (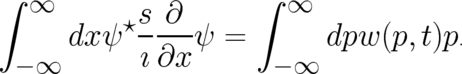
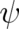 , defined by
, defined by 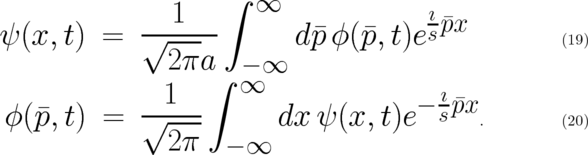
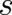 , introduced in Eq. (14), has the dimension of an action, which means that
, introduced in Eq. (14), has the dimension of an action, which means that 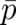 has the
dimension of a momentum. Performing the Fourier transform one finds that the momentum probability density
may be written as
has the
dimension of a momentum. Performing the Fourier transform one finds that the momentum probability density
may be written as
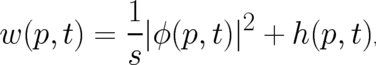
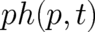 has to vanish. Using Parseval’s formula and the fact that both
has to vanish. Using Parseval’s formula and the fact that both
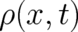 and
and 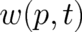 are normalized to unity we find that the integral of
are normalized to unity we find that the integral of 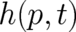 has to vanish
too.
has to vanish
too.
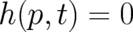 to characteristic relations of the
quantum mechanical formalism. However, the function
to characteristic relations of the
quantum mechanical formalism. However, the function 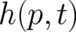 , as well as the probability
density
, as well as the probability
density 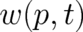 we are finally interested in, is still unknown, because the validity of the
deterministic relation (
we are finally interested in, is still unknown, because the validity of the
deterministic relation (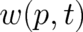 . We shall come back to the problem of the determination of
. We shall come back to the problem of the determination of 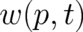 in
section
in
section