![I [ρ ]](soqweb358x.png) is defined
by
is defined
by
A second measure of disorder, besides entropy, exists which is called Fisher information [9]. The importance of
this second type of “entropy”for the mathematical form of the laws of physics - in particular for the terms
related to the kinetic energy - has been stressed in a number of publications by Frieden and coworkers [10, 11]
and has been studied further by Hall [16], Reginatto [36] and others. The Fisher functional ![I [ρ ]](soqweb358x.png) is defined
by
is defined
by
![∫ ( ′ )2
ρ (x )
I [ρ ] = dx ρ (x ) -------- ,
ρ (x )](soqweb359x.png) | (48) |
where 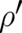 denotes
denotes 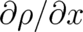 in the present one-dimensional case, and the
in the present one-dimensional case, and the 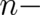 component
vector
component
vector 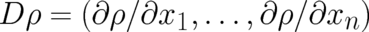 if
if 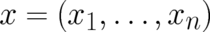 .
Since the time variable
.
Since the time variable 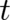 does not play an important role it will frequently be suppressed in this
section.
does not play an important role it will frequently be suppressed in this
section.
The Boltzmann-Shannon entropy (44) and the Fisher information (48) have a number of crucial statistical properties in common. We mention here, for future reference, only the most important one, namely the composition law (41); a more complete list of common properties may be found in the literature [48]). Using the notation introduced in section 7 [see the text preceeding Eq. (41)] it is easy to see that Eq. (48) fulfills the relation
![I [ρ ρ ] = I (1 )[ρ ] + I (2 )[ρ ],
1 2 1 2](soqweb366x.png) | (49) |
in analogy to Eq. (41) for the entropy 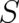 . The most obvious difference between (44) and (48) is the fact
that (48) contains a derivative while (44) does not. As a consequence, extremizing these two functionals yields
fundamentally different equations for
. The most obvious difference between (44) and (48) is the fact
that (48) contains a derivative while (44) does not. As a consequence, extremizing these two functionals yields
fundamentally different equations for 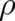 , namely a differential equation for the Fisher functional
, namely a differential equation for the Fisher functional 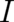 and an
algebraic equation for the entropy functional
and an
algebraic equation for the entropy functional 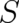 .
.
The two measures of disorder, 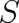 and
and 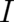 , are related to each other. To find this relation, it is
necessary to introduce a generalized version of (44), the so-called “relative entropy”. It is defined
by
, are related to each other. To find this relation, it is
necessary to introduce a generalized version of (44), the so-called “relative entropy”. It is defined
by
![∫
ρ (x )
--------
G [ρ, α ] = - dx ρ (x ) ln ,
α (x )](soqweb373x.png) | (50) |
where 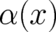 is a given probability density, sometimes referred to as the “prior” [the constant
is a given probability density, sometimes referred to as the “prior” [the constant 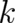 in
Eq. (44) has been suppressed here]. It provides a reference point for the unknown
in
Eq. (44) has been suppressed here]. It provides a reference point for the unknown 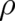 ; the best choice for
; the best choice for 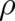 is
to be determined from the requirement of maximal relative entropy
is
to be determined from the requirement of maximal relative entropy ![G [ρ, α ]](soqweb378x.png) under given constraints,
where
under given constraints,
where 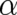 represents the state of affairs (or of our knowledge of the state of affairs) prior to consideration of
the constraints. The quantity
represents the state of affairs (or of our knowledge of the state of affairs) prior to consideration of
the constraints. The quantity ![- G [ρ, α ]](soqweb380x.png) agrees with the “Kullback-Leibler distance” between two
probability densities
agrees with the “Kullback-Leibler distance” between two
probability densities 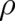 and
and 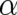 [28].
[28].
It has been pointed out that “all entropies are relative entropies” [6]. In fact, all physical quantities need
reference points in order to become observables. The Boltzmann-Shannon entropy (44) is no exception. In this
case, the ‘probability density’ 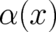 is a number of value
is a number of value 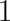 , and of the same dimension as
, and of the same dimension as 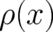 ; it
describes absence of any knowledge or a completely disordered state. We mention also two other more technical
points which imply the need for relative entropies. The first is the requirement to perform invariant variable
transformations in the sample space [6], the second is the requirement to perform a smooth transition from
discrete to continuous probabilities [18].
; it
describes absence of any knowledge or a completely disordered state. We mention also two other more technical
points which imply the need for relative entropies. The first is the requirement to perform invariant variable
transformations in the sample space [6], the second is the requirement to perform a smooth transition from
discrete to continuous probabilities [18].
Thus, the concept of relative entropies is satisfying from a theoretical point of view. On the other hand it
seems to be useless from a practical point of view since it requires - except in the trivial limit 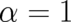 -
knowledge of a new function
-
knowledge of a new function 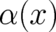 which is in general just as unknown as the original unknown function
which is in general just as unknown as the original unknown function
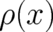 . A way out of this dilemma is to identify
. A way out of this dilemma is to identify 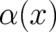 with a function
with a function 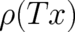 , which can be
obtained from
, which can be
obtained from 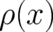 by replacing the argument
by replacing the argument 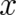 by a transformed argument
by a transformed argument 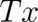 . In this way we
obtain from (50) a quantity
. In this way we
obtain from (50) a quantity ![G [ρ; pT ]](soqweb394x.png) which is a functional of the relevant function
which is a functional of the relevant function 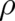 alone; in
addition it is an ordinary function of the parameters
alone; in
addition it is an ordinary function of the parameters 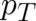 characterizing the transformation. The physical
meaning of the relative entropy remains unchanged, the requirement of maximal relative entropy
characterizing the transformation. The physical
meaning of the relative entropy remains unchanged, the requirement of maximal relative entropy
![G [ρ; p ]
T](soqweb397x.png) becomes a condition for the variation of
becomes a condition for the variation of 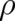 in the sample space between the points
in the sample space between the points 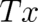 and
and 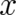 .
.
If further consideration is restricted to translations 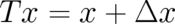 (it would be interesting to
investigate other transformations, in particular if the sample space agrees with the configuration space) then the
relative entropy is written as
(it would be interesting to
investigate other transformations, in particular if the sample space agrees with the configuration space) then the
relative entropy is written as
![∫
-----ρ-(x--)-----
G [ρ; Δx ] = - dx ρ (x ) ln .
ρ (x + Δx )](soqweb402x.png) | (51) |
Expanding the integrand on the r.h.s. of (51) up to terms of second order in 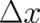 and using the fact that
and using the fact that 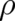 and
and 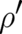 have to vanish at infinity one obtains the relation
have to vanish at infinity one obtains the relation
![2
. Δx
G [ρ; Δx ] = - ------- I [ρ ].
2](soqweb406x.png) | (52) |
This, then is the required relation between the relative entropy 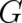 and and the Fisher information
and and the Fisher information 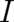 ; it is
valid only for sufficiently small
; it is
valid only for sufficiently small 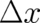 . The relative entropy
. The relative entropy ![G [ρ; Δx ]](soqweb410x.png) cannot be positive. Considered
as a function of
cannot be positive. Considered
as a function of 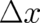 it has a maximum at
it has a maximum at 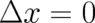 (taking its maximal value
(taking its maximal value  )
provided
)
provided 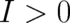 . This means that the principle of maximal entropy implies no change at
all relative to an arbitrary reference density. This provides no criterion for
. This means that the principle of maximal entropy implies no change at
all relative to an arbitrary reference density. This provides no criterion for 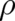 since it holds for
arbitrary
since it holds for
arbitrary 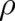 . But if (52) is considered, for fixed
. But if (52) is considered, for fixed 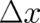 , as a functional of
, as a functional of 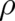 , the principle of
maximal entropy implies, as a criterion for the spatial variation of
, the principle of
maximal entropy implies, as a criterion for the spatial variation of 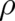 , a principle of minimal Fisher
information.
, a principle of minimal Fisher
information.
Thus, from this overview (see Frieden‘s book [11] for more details and several other interesting aspects) we
would conclude that the principle of minimal Fisher information should not be considered as a completely new
and exotic matter. Rather it should be considered as an extension or generalization of the classical principle of
maximal disorder to a situation where a spatially varying probability exists, which contributes to disorder. This
requires, in particular, that this probability density is to be determined from a differential equation and not
from an algebraic equation. We conclude that the principle of minimal Fisher 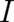 is very well
suited for our present purpose. As a next step we have to set up proper constraints for the extremal
principle.
is very well
suited for our present purpose. As a next step we have to set up proper constraints for the extremal
principle.