7 Entropy as a measure of disorder ?
How then to determine the unknown function 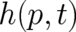 [and
[and 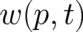 ] ? According to the last section,
all the required information on
] ? According to the last section,
all the required information on 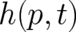 may be obtained from a knowledge of the term
may be obtained from a knowledge of the term 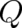 in the
differential equation (26) for
in the
differential equation (26) for 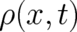 . We shall try to solve this problem my means of the following
two-step strategy: (i) Find an additional physical condition for the fundamental probability density
. We shall try to solve this problem my means of the following
two-step strategy: (i) Find an additional physical condition for the fundamental probability density
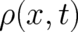 , (ii) determine the shape of
, (ii) determine the shape of 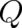 [as well as that of
[as well as that of 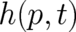 and
and 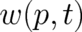 ] from this
condition.
] from this
condition.
At this point it may be useful to recall the way probability densities are determined in classical statistical
physics. After all, the present class of theories is certainly not of a deterministic nature and belongs
fundamentally to the same class of statistical (i.e. incomplete with regard to the description of single events)
theories as classical statistical physics; no matter how important the remaining differences may
be.
The physical condition for 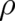 which determines the behavior of ensembles in classical statistical physics is
the principle of maximal (Boltzmann) entropy. It agrees essentially with the information-theoretic measure of
disorder introduced by Shannon [41]. Using this principle both the micro-canonical and the canonical
distribution of statistical thermodynamics may be derived under appropriate constraints. Let us discuss this
classical extremal principle in some detail in order to see if it can be applied, after appropriate modifications,
to the present problem. This question also entails a comparison of different types of statistical
theories.
which determines the behavior of ensembles in classical statistical physics is
the principle of maximal (Boltzmann) entropy. It agrees essentially with the information-theoretic measure of
disorder introduced by Shannon [41]. Using this principle both the micro-canonical and the canonical
distribution of statistical thermodynamics may be derived under appropriate constraints. Let us discuss this
classical extremal principle in some detail in order to see if it can be applied, after appropriate modifications,
to the present problem. This question also entails a comparison of different types of statistical
theories.
The Boltzmann-Shannon entropy is defined as a functional ![S [ρ ]](soqweb296x.png) of an arbitrary probability density
of an arbitrary probability density 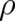 .
The statistical properties characterizing disorder, which may be used to define this functional, are discussed
in many publications [5], [22]. Only one of these conditions will, for later use, be written down
here, namely the so-called “composition law”: Let us assume that
.
The statistical properties characterizing disorder, which may be used to define this functional, are discussed
in many publications [5], [22]. Only one of these conditions will, for later use, be written down
here, namely the so-called “composition law”: Let us assume that 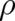 may be written in the form
may be written in the form
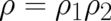 where
where 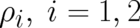 depends only on points in a subspace
depends only on points in a subspace 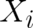 of our
of our
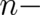 dimensional sample space
dimensional sample space 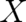 and let us further assume that
and let us further assume that 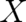 is the direct product of
is the direct product of 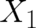 and
and 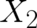 . Thus, this system consists of two independent subsystems. Then, the composition law is given
by
. Thus, this system consists of two independent subsystems. Then, the composition law is given
by
![(1 ) (2 )
S [ρ1 ρ2 ] = S [ρ1 ] + S [ρ2 ],](soqweb307x.png) | (41) |
where 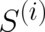 operates only on
operates only on 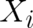 .
.
For a countable sample space with events labeled by indices 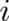 from an index set
from an index set 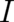 and probabilities
and probabilities
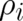 , the entropy is given by
, the entropy is given by
![∑
S [ρ ] = - k ρi ln ρi,
i∈I](soqweb313x.png) | (42) |
where 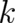 is a constant. To obtain meaningful results the extrema of (42) under appropriate constraints,
or subsidiary conditions, must be found. The simplest constraint is the normalization condition
is a constant. To obtain meaningful results the extrema of (42) under appropriate constraints,
or subsidiary conditions, must be found. The simplest constraint is the normalization condition
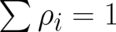 . In this case the extrema of the function
. In this case the extrema of the function
![( )
∑ ∑
F [ρ, λ ] = - k ρ ln ρ + λ ( ρ - 1 )
i i i
i∈I i∈I](soqweb316x.png) | (43) |
with respect to the variables 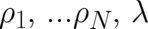 must be calculated. One obtains the reasonable result that
the minimal value of
must be calculated. One obtains the reasonable result that
the minimal value of ![F [ρ, λ ]](soqweb318x.png) is
is  (one of the
(one of the 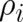 equal to
equal to 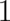 , all other equal to
, all other equal to  ) and the
maximal value is
) and the
maximal value is 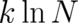 (all
(all 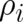 equal,
equal, 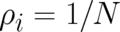 ).
).
For most problems of physical interest the sample space is non-denumerable. A straightforward generalization
of Eq. (42) is given by
![∫
S [ρ ] = - k dx ρ (x ) ln ρ (x ),](soqweb326x.png) | (44) |
where the symbol 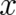 denotes now a point in the appropriate (generally
denotes now a point in the appropriate (generally 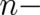 dimensional) sample
space. There are some problems inherent in the this straightforward transition to a continuous set of
events which will be mentioned briefly in the next section. Let us put aside this problems for the
moment and ask if (44) makes sense from a physical point of view. For non-denumerable problems the
principle of maximal disorder leads to a variational problem and the method of Lagrange multipliers
may still be used to combine the requirement of maximal entropy with other defining properties
(constraints). An important constraint is the property of constant temperature which leads to the condition
that the expectation value of the possible energy values
dimensional) sample
space. There are some problems inherent in the this straightforward transition to a continuous set of
events which will be mentioned briefly in the next section. Let us put aside this problems for the
moment and ask if (44) makes sense from a physical point of view. For non-denumerable problems the
principle of maximal disorder leads to a variational problem and the method of Lagrange multipliers
may still be used to combine the requirement of maximal entropy with other defining properties
(constraints). An important constraint is the property of constant temperature which leads to the condition
that the expectation value of the possible energy values 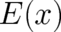 is given by a fixed number
is given by a fixed number
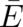 ,
,
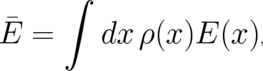 | (45) |
If, in addition, normalizability is implemented as a defining property, then the true distribution should be an
extremum of the functional
![∫ ∫ ∫
K [ρ ] = - k dx ρ (x ) ln ρ (x )- λ dx ρ (x )E (x )- λ dx ρ (x ).
2 1](soqweb332x.png) | (46) |
It is easy to see that the well-known canonical distribution of statistical physics is indeed an extremum of
![K [ρ ]](soqweb333x.png) . Can we use a properly adapted version of this powerful principle of maximal disorder (entropy) to
solve our present problem ?
. Can we use a properly adapted version of this powerful principle of maximal disorder (entropy) to
solve our present problem ?
Let us compare the class of theories derived in section 5 with classical theories like (46). This may
be of interest also in view of a possible identification of ’typical quantum mechanical properties’
of statistical theories. We introduce for clarity some notation, based on properties of the sample
space. Classical statistical physics theories like (46) will be referred to as ”phase space theories”.
The class of statistical theories, derived in section 5, will be referred to as ”configuration space
theories”.
The most fundamental difference between phase space theories and configuration space theories concerns the
physical meaning of the coordinates. The coordinates 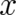 of phase space theories are (generally
time-dependent) labels for particle properties. In contrast, configuration space theories are field theories;
individual particles do not exist and the (in our case one-dimensional) coordinates
of phase space theories are (generally
time-dependent) labels for particle properties. In contrast, configuration space theories are field theories;
individual particles do not exist and the (in our case one-dimensional) coordinates 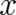 are points in
space.
are points in
space.
A second fundamental difference concerns the dimension of the sample space. Elementary events in phase
space theories are points in phase space (of dimension 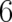 for a
for a  particle system) including
configuration-space and momentum-space (particle) coordinates while the elementary events of configuration
space theories are (space) points in configuration space (which would be of dimension
particle system) including
configuration-space and momentum-space (particle) coordinates while the elementary events of configuration
space theories are (space) points in configuration space (which would be of dimension 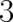 for a
for a  particle
system in three spatial dimensions). This fundamental difference is a consequence of a (generally nonlocal)
dependence between momentum coordinates and space-time points contained in the postulates of the present
theory, in particular in the postulated form of the probability current [see (7)]. This assumption, a probability
current, which takes the form of a gradient of a function
particle
system in three spatial dimensions). This fundamental difference is a consequence of a (generally nonlocal)
dependence between momentum coordinates and space-time points contained in the postulates of the present
theory, in particular in the postulated form of the probability current [see (7)]. This assumption, a probability
current, which takes the form of a gradient of a function 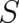 (multiplied by
(multiplied by 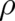 ) is a key feature
distinguishing configuration space theories, as potential quantum-like theories, from the familiar
(many body) phase space theories. The existence of this dependence per se is not an exclusive
feature of quantum mechanics, it is a property of all theories belonging to the configuration class,
including the theory characterized by
) is a key feature
distinguishing configuration space theories, as potential quantum-like theories, from the familiar
(many body) phase space theories. The existence of this dependence per se is not an exclusive
feature of quantum mechanics, it is a property of all theories belonging to the configuration class,
including the theory characterized by 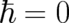 , which will be referred to as ”classical limit
theory”. What distinguishes the classical limit theory from quantum mechanics is the particular
form of this dependence; for the former it is given by a conventional functional relationship (as
discussed in section 4) for the latter it is given by a nonlocal relationship whose form is still to be
determined.
, which will be referred to as ”classical limit
theory”. What distinguishes the classical limit theory from quantum mechanics is the particular
form of this dependence; for the former it is given by a conventional functional relationship (as
discussed in section 4) for the latter it is given by a nonlocal relationship whose form is still to be
determined.
This dependence is responsible for the fact that no ”global” condition [like (45) for the canonical
distribution] must be introduced for the present theory in order to guarantee conservation of energy in the mean
- this conservation law can be guaranteed ”locally” for arbitrary theories of the configuration class by adjusting
the relation between 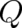 (the form of the dynamic equation) and
(the form of the dynamic equation) and 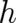 (the definition of expectation values). In
phase space theories the form of the dynamical equations is fixed (given by the deterministic equations of
classical mechanics). Under constraints like (45) the above principle of maximal disorder creates - basically by
selecting appropriate initial conditions - those systems which belong to a particular energy; for non-stationary
conditions the deterministic differential equations of classical mechanics guarantee then that energy
conservation holds for all times. In contrast, in configuration space theories there are no initial
conditions (for particles). The conditions which are at our disposal are the mathematical form of the
expectation values (the function
(the definition of expectation values). In
phase space theories the form of the dynamical equations is fixed (given by the deterministic equations of
classical mechanics). Under constraints like (45) the above principle of maximal disorder creates - basically by
selecting appropriate initial conditions - those systems which belong to a particular energy; for non-stationary
conditions the deterministic differential equations of classical mechanics guarantee then that energy
conservation holds for all times. In contrast, in configuration space theories there are no initial
conditions (for particles). The conditions which are at our disposal are the mathematical form of the
expectation values (the function 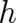 ) and/or the mathematical form of the differential equation (the
function
) and/or the mathematical form of the differential equation (the
function 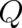 ). Thus, if something like the principle of maximal disorder can be used in the present
theory it will determine the form of the differential equation for
). Thus, if something like the principle of maximal disorder can be used in the present
theory it will determine the form of the differential equation for 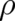 rather than the explicit form of
rather than the explicit form of
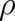 .
.
These considerations raise some doubt as to the usefulness of an measure of disorder like the entropy (44) -
which depends essentially on 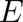 instead of
instead of 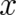 and does not contain derivatives of
and does not contain derivatives of 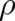 - for the
present problem. We may still look for an information theoretic extremal principle of the general
form
- for the
present problem. We may still look for an information theoretic extremal principle of the general
form
![∑
I [ρ ] + λlCl [ρ ] → extremum.
l](soqweb352x.png) | (47) |
Here, the functional ![I [ρ ]](soqweb353x.png) attains its maximal value for the function
attains its maximal value for the function 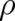 which describes - under
given constraints
which describes - under
given constraints ![Cl [ρ ]](soqweb355x.png) - the maximal disorder. But
- the maximal disorder. But ![I [ρ ]](soqweb356x.png) will differ from the entropy
functional and appropriate constraints
will differ from the entropy
functional and appropriate constraints ![Cl [ρ ]](soqweb357x.png) , reflecting the local character of the present
problem, have still to be found. Both terms in (47) are at our disposal and will be defined in the next
sections.
, reflecting the local character of the present
problem, have still to be found. Both terms in (47) are at our disposal and will be defined in the next
sections.
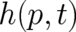 [and
[and 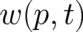 ] ? According to the last section,
all the required information on
] ? According to the last section,
all the required information on 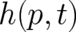 may be obtained from a knowledge of the term
may be obtained from a knowledge of the term 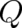 in the
differential equation (26) for
in the
differential equation (26) for 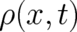 . We shall try to solve this problem my means of the following
two-step strategy: (i) Find an additional physical condition for the fundamental probability density
. We shall try to solve this problem my means of the following
two-step strategy: (i) Find an additional physical condition for the fundamental probability density
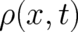 , (ii) determine the shape of
, (ii) determine the shape of 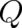 [as well as that of
[as well as that of 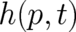 and
and 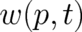 ] from this
condition.
] from this
condition.
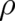 which determines the behavior of ensembles in classical statistical physics is
the principle of
which determines the behavior of ensembles in classical statistical physics is
the principle of ![S [ρ ]](soqweb296x.png) of an arbitrary probability density
of an arbitrary probability density 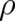 .
The statistical properties characterizing disorder, which may be used to define this functional, are discussed
in many publications
.
The statistical properties characterizing disorder, which may be used to define this functional, are discussed
in many publications 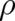 may be written in the form
may be written in the form
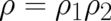 where
where 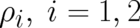 depends only on points in a subspace
depends only on points in a subspace 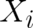 of our
of our
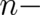 dimensional sample space
dimensional sample space 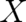 and let us further assume that
and let us further assume that 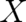 is the direct product of
is the direct product of 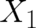 and
and 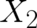 . Thus, this system consists of two independent subsystems. Then, the composition law is given
by
. Thus, this system consists of two independent subsystems. Then, the composition law is given
by
![(1 ) (2 )
S [ρ1 ρ2 ] = S [ρ1 ] + S [ρ2 ],](soqweb307x.png)
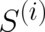 operates only on
operates only on 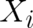 .
.
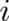 from an index set
from an index set 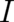 and probabilities
and probabilities
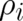 , the entropy is given by
, the entropy is given by
![∑
S [ρ ] = - k ρi ln ρi,
i∈I](soqweb313x.png)
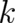 is a constant. To obtain meaningful results the extrema of (
is a constant. To obtain meaningful results the extrema of (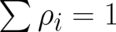 . In this case the extrema of the function
. In this case the extrema of the function
![( )
∑ ∑
F [ρ, λ ] = - k ρ ln ρ + λ ( ρ - 1 )
i i i
i∈I i∈I](soqweb316x.png)
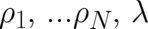 must be calculated. One obtains the reasonable result that
the minimal value of
must be calculated. One obtains the reasonable result that
the minimal value of ![F [ρ, λ ]](soqweb318x.png) is
is  (one of the
(one of the 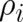 equal to
equal to 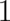 , all other equal to
, all other equal to  ) and the
maximal value is
) and the
maximal value is 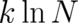 (all
(all 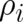 equal,
equal, 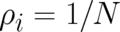 ).
).
![∫
S [ρ ] = - k dx ρ (x ) ln ρ (x ),](soqweb326x.png)
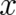 denotes now a point in the appropriate (generally
denotes now a point in the appropriate (generally 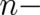 dimensional) sample
space. There are some problems inherent in the this straightforward transition to a continuous set of
events which will be mentioned briefly in the next section. Let us put aside this problems for the
moment and ask if (
dimensional) sample
space. There are some problems inherent in the this straightforward transition to a continuous set of
events which will be mentioned briefly in the next section. Let us put aside this problems for the
moment and ask if (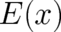 is given by a fixed number
is given by a fixed number
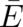 ,
,
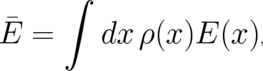
![∫ ∫ ∫
K [ρ ] = - k dx ρ (x ) ln ρ (x )- λ dx ρ (x )E (x )- λ dx ρ (x ).
2 1](soqweb332x.png)
![K [ρ ]](soqweb333x.png) . Can we use a properly adapted version of this powerful principle of maximal disorder (entropy) to
solve our present problem ?
. Can we use a properly adapted version of this powerful principle of maximal disorder (entropy) to
solve our present problem ?
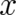 of phase space theories are (generally
time-dependent) labels for particle properties. In contrast, configuration space theories are field theories;
individual particles do not exist and the (in our case one-dimensional) coordinates
of phase space theories are (generally
time-dependent) labels for particle properties. In contrast, configuration space theories are field theories;
individual particles do not exist and the (in our case one-dimensional) coordinates 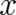 are points in
space.
are points in
space.
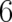 for a
for a  particle system) including
configuration-space
particle system) including
configuration-space 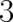 for a
for a  particle
system in three spatial dimensions). This fundamental difference is a consequence of a (generally nonlocal)
dependence between momentum coordinates and space-time points contained in the postulates of the present
theory, in particular in the postulated form of the probability current [see (
particle
system in three spatial dimensions). This fundamental difference is a consequence of a (generally nonlocal)
dependence between momentum coordinates and space-time points contained in the postulates of the present
theory, in particular in the postulated form of the probability current [see (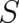 (multiplied by
(multiplied by 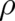 ) is a key feature
distinguishing configuration space theories, as potential quantum-like theories, from the familiar
(many body) phase space theories. The existence of this dependence per se is not an exclusive
feature of quantum mechanics, it is a property of all theories belonging to the configuration class,
including the theory characterized by
) is a key feature
distinguishing configuration space theories, as potential quantum-like theories, from the familiar
(many body) phase space theories. The existence of this dependence per se is not an exclusive
feature of quantum mechanics, it is a property of all theories belonging to the configuration class,
including the theory characterized by 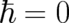 , which will be referred to as ”classical limit
theory”. What distinguishes the classical limit theory from quantum mechanics is the particular
form of this dependence; for the former it is given by a conventional functional relationship (as
discussed in section
, which will be referred to as ”classical limit
theory”. What distinguishes the classical limit theory from quantum mechanics is the particular
form of this dependence; for the former it is given by a conventional functional relationship (as
discussed in section 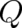 (the form of the dynamic equation) and
(the form of the dynamic equation) and 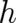 (the definition of expectation values). In
phase space theories the form of the dynamical equations is fixed (given by the deterministic equations of
classical mechanics). Under constraints like (
(the definition of expectation values). In
phase space theories the form of the dynamical equations is fixed (given by the deterministic equations of
classical mechanics). Under constraints like (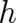 ) and/or the mathematical form of the differential equation (the
function
) and/or the mathematical form of the differential equation (the
function 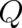 ). Thus, if something like the principle of maximal disorder can be used in the present
theory it will determine the form of the differential equation for
). Thus, if something like the principle of maximal disorder can be used in the present
theory it will determine the form of the differential equation for 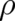 rather than the explicit form of
rather than the explicit form of
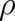 .
.
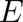 instead of
instead of 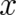 and does not contain derivatives of
and does not contain derivatives of 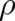 - for the
present problem. We may still look for an information theoretic extremal principle of the general
form
- for the
present problem. We may still look for an information theoretic extremal principle of the general
form
![∑
I [ρ ] + λlCl [ρ ] → extremum.
l](soqweb352x.png)
![I [ρ ]](soqweb353x.png) attains its maximal value for the function
attains its maximal value for the function 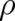 which describes - under
given constraints
which describes - under
given constraints ![Cl [ρ ]](soqweb355x.png) - the maximal disorder. But
- the maximal disorder. But ![I [ρ ]](soqweb356x.png) will differ from the entropy
functional and appropriate constraints
will differ from the entropy
functional and appropriate constraints ![Cl [ρ ]](soqweb357x.png) , reflecting the local character of the present
problem, have still to be found. Both terms in (
, reflecting the local character of the present
problem, have still to be found. Both terms in (