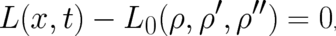
It will be convenient in the course of the following calculations to write the differential equation (26) in the form
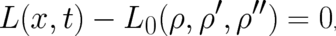 | (53) |
where  is given by (25) and
is given by (25) and  is defined by
is defined by
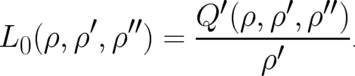 | (54) |
In (54) it has been assumed that 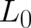 does not depend explicitely on
does not depend explicitely on 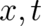 , that the problem is basically of
a time-independent nature, and that no higher derivatives with respect to
, that the problem is basically of
a time-independent nature, and that no higher derivatives with respect to 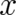 than
than 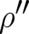 occur.
This last assumption is in agreement with the mathematical form of all fundamental differential
equations of physics; we shall come back to this point later. Our task is to determine the functional
form of
occur.
This last assumption is in agreement with the mathematical form of all fundamental differential
equations of physics; we shall come back to this point later. Our task is to determine the functional
form of 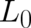 , with respect to the variables
, with respect to the variables 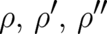 , using a general statistical extremal
principle. As a consequence of the general nature of this problem we do not expect the solution to
depend on the particular form of
, using a general statistical extremal
principle. As a consequence of the general nature of this problem we do not expect the solution to
depend on the particular form of 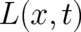 . For the same reason
. For the same reason 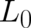 does not depend on
does not depend on
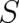 .
.
We tentatively formulate a principle of maximal disorder of the form (47) and identify ![I [ρ ]](soqweb434x.png) with the
Fisher functional (48). Then, the next step is to find a proper constraint
with the
Fisher functional (48). Then, the next step is to find a proper constraint ![C [ρ ]](soqweb435x.png) . In accord with general
statistical principles the prescribed quantity should have the form of a statistical average. A second condition is
that our final choice should be as similar to the classical requirement (45) as possible. Adopting these criteria
one is led more or less automatically to the constraint
. In accord with general
statistical principles the prescribed quantity should have the form of a statistical average. A second condition is
that our final choice should be as similar to the classical requirement (45) as possible. Adopting these criteria
one is led more or less automatically to the constraint
![C [ρ ] = 0,](soqweb436x.png) | (55) |
where
![∫
[ ]
C [ρ ] = dx ρ L (x, t ) - L (ρ, ρ ′, ρ ′′) .
0](soqweb437x.png) | (56) |
Our guideline in setting up this criterion has been the idea of a prescribed value of the average
energy; the new term 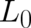 plays the role of an additional contribution to the energy. For
plays the role of an additional contribution to the energy. For
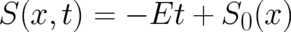 and
and 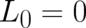 the constraint (55) agrees with (45) provided
the ‘classical‘ identification of
the constraint (55) agrees with (45) provided
the ‘classical‘ identification of 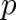 with the gradient of
with the gradient of 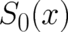 is performed [see (8)]. The most striking
difference between (45) and (55) is the fact that the quantity
is performed [see (8)]. The most striking
difference between (45) and (55) is the fact that the quantity 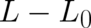 in (56), whose expectation value
yields the constraint, is not defined independently from the statistics [like
in (56), whose expectation value
yields the constraint, is not defined independently from the statistics [like 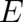 in (45)] but depends itself on
in (45)] but depends itself on
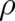 (and its derivatives up to second order). This aspect of non-classical theories has already been discussed in
section 5.
(and its derivatives up to second order). This aspect of non-classical theories has already been discussed in
section 5.
Let us try to apply the mathematical apparatus of variational calculus [49] to the constraint problem (47)
with the ”‘entropy”’ functional ![I [ρ ]](soqweb446x.png) defined by (48) and a single constraint defined by (55) and (56)
(there is no normalization condition here because we do not want to exclude potentially meaningful
non-normalizable states from the consideration). Here we encounter immediately a first problem which is
due to the fact that our problem consists in the determination of an unknown function
defined by (48) and a single constraint defined by (55) and (56)
(there is no normalization condition here because we do not want to exclude potentially meaningful
non-normalizable states from the consideration). Here we encounter immediately a first problem which is
due to the fact that our problem consists in the determination of an unknown function 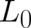 of
of
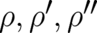 . This function appears in the differential equation and in the subsidiary condition for
the variational problem. Thus, our task is to identify from a variational problem the functional
form of a constraint defining this variational problem. Variational calculus, starts, of course, from
constraints whose functional forms are fixed; these fixed functionals are used to derive differential
equations for the variable
. This function appears in the differential equation and in the subsidiary condition for
the variational problem. Thus, our task is to identify from a variational problem the functional
form of a constraint defining this variational problem. Variational calculus, starts, of course, from
constraints whose functional forms are fixed; these fixed functionals are used to derive differential
equations for the variable 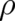 . Thus, whenever the calculus of variations is applied, the function
. Thus, whenever the calculus of variations is applied, the function
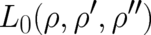 must be considered as unknown but fixed. We shall have to find a way to
’transform’ the condition for the variation of
must be considered as unknown but fixed. We shall have to find a way to
’transform’ the condition for the variation of 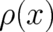 in a corresponding condition for the variation of
in a corresponding condition for the variation of
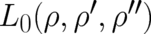 .
.
The variational calculation defined above belongs to a class of ’isoperimetric’ variational problems which can
be solved using the standard method of Lagrange multipliers, provided certain mathematical conditions are
fulfilled [49]. Analyzing the situation we encounter here a second problem, which is in fact related to the first.
Let us briefly recall the way the variational problem (47) is solved, in particular with regard to the role of the
Lagrange multipliers 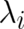 [49]. Given the problem to find an extremal
[49]. Given the problem to find an extremal 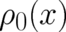 of
of ![I [ρ ]](soqweb455x.png) under
under 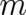 constraints of the form
constraints of the form ![Ci [ρ ] = 0](soqweb457x.png) and two prescribed values of
and two prescribed values of 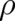 at the boundaries, one
proceeds as follows. The Euler-Lagrange equation belonging to the functional (47) is solved. The
general solution for
at the boundaries, one
proceeds as follows. The Euler-Lagrange equation belonging to the functional (47) is solved. The
general solution for 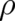 depends (besides on
depends (besides on 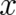 ) on two integration constants, say
) on two integration constants, say 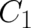 and
and
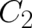 , and on the
, and on the 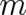 Lagrange multipliers
Lagrange multipliers 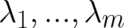 . To obtain the final extremal
. To obtain the final extremal
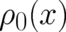 , these
, these 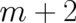 constants have to be determined from the two boundary values
and the
constants have to be determined from the two boundary values
and the 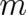 constraints (which are differential equations for isoperimetric problems). This is
exactly the way the calculation has been performed (even though a simpler form of the constraints
has been used) in the classical case. For the present problem, however, this procedure is useless,
since we do not want the constraints to determine the shape of individual solutions but rather
the functional form of a term in the differential equation, which is then the same for all solutions.
For that reason the ‘normal‘ variational problem (47) does not work (we shall come back to a
mathematical definition of ‘normal‘ and ‘abnormal‘ shortly). This means that the classical principle
of maximal entropy, as discussed in section 7, cannot be taken over literally to the non-classical
domain.
constraints (which are differential equations for isoperimetric problems). This is
exactly the way the calculation has been performed (even though a simpler form of the constraints
has been used) in the classical case. For the present problem, however, this procedure is useless,
since we do not want the constraints to determine the shape of individual solutions but rather
the functional form of a term in the differential equation, which is then the same for all solutions.
For that reason the ‘normal‘ variational problem (47) does not work (we shall come back to a
mathematical definition of ‘normal‘ and ‘abnormal‘ shortly). This means that the classical principle
of maximal entropy, as discussed in section 7, cannot be taken over literally to the non-classical
domain.
For the same reason, no subsidiary conditions can be taken into account in the calculations reported by Frieden [10] and by Reginatto [36]. In these works, a different route is chosen to obtain Schrödingers equation; in contrast to the present work (see below) the Fisher functional is added as a new term to a classical Lagrangian and the particular form of this new term is justified by introducing a new ”‘principle of extreme physical information”’ [12].
A variational problem is called ‘normal‘ if an extremal of the functional ![I [ρ ] + λ1C [ρ ]](soqweb468x.png) (here we
restrict ourselves to the present case of a single constraint) exists which is not at the same time an extremal of
the constraint functional
(here we
restrict ourselves to the present case of a single constraint) exists which is not at the same time an extremal of
the constraint functional ![C [ρ ]](soqweb469x.png) . If this is not the case, i.e. if the extremal is at the same time
an extremal of
. If this is not the case, i.e. if the extremal is at the same time
an extremal of ![C [ρ ]](soqweb470x.png) , then the problem is called ‘abnormal‘ [49]. Then, the usual derivation
becomes invalid and the condition (47) must be replaced by the condition of extremal
, then the problem is called ‘abnormal‘ [49]. Then, the usual derivation
becomes invalid and the condition (47) must be replaced by the condition of extremal ![C [ρ ]](soqweb471x.png) alone,
alone,
![λ C [ρ ] → extremum,
1](soqweb472x.png) | (57) |
which then yields ![δC [ρ ] = 0](soqweb473x.png) as only remaining condition to determine the extremal. This type of
problem is also sometimes referred to as ”rigid”; the original formulation (47) may be extended to include the
abnormal case by introducing a second Lagrange multiplier [49].
as only remaining condition to determine the extremal. This type of
problem is also sometimes referred to as ”rigid”; the original formulation (47) may be extended to include the
abnormal case by introducing a second Lagrange multiplier [49].
We conclude that our present problem should be treated as an abnormal variational problem since we
thereby get rid of our main difficulty, namely the unwanted dependence of individual solutions on
Lagrange multipliers [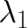 drops actually out of Eq. (57)]. A somewhat dissatisfying (at first sight)
feature of this approach is the fact that the Fisher functional
drops actually out of Eq. (57)]. A somewhat dissatisfying (at first sight)
feature of this approach is the fact that the Fisher functional ![I [ρ ]](soqweb475x.png) itself does no longer take
part in the variational procedure; the original idea of implementing maximal statistical disorder
seems to have been lost. But it turns out that we shall soon recover the Fisher
itself does no longer take
part in the variational procedure; the original idea of implementing maximal statistical disorder
seems to have been lost. But it turns out that we shall soon recover the Fisher 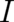 in the course
of the following calculation. The vanishing of the first variation of
in the course
of the following calculation. The vanishing of the first variation of ![C [ρ ]](soqweb477x.png) , written explicitely
as
, written explicitely
as
![∫
[ ′ ′′ ]
δC [ρ ] = δ dx ρ L (x, t ) - L0 (ρ, ρ , ρ ) = 0,](soqweb478x.png) | (58) |
means that (for fixed 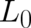 ) the spatial variation of
) the spatial variation of 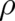 should extremize (minimize) the average
value of the deviation from
should extremize (minimize) the average
value of the deviation from 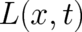 . This requirement is [as a condition for
. This requirement is [as a condition for 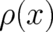 ] in
agreement with the principle of minimal Fisher information as a special realization of the requirement of
maximal disorder. Eq. (58) defines actually a Lagrangian for
] in
agreement with the principle of minimal Fisher information as a special realization of the requirement of
maximal disorder. Eq. (58) defines actually a Lagrangian for 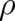 and yields as Euler-Lagrange
equations a differential equation for
and yields as Euler-Lagrange
equations a differential equation for 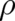 . When this equation is derived the task of variational
calculus is finished. On the other hand, we know that
. When this equation is derived the task of variational
calculus is finished. On the other hand, we know that 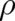 obeys also Eq. (53). Both differential
equations must agree and this fact yields a condition for our unknown function
obeys also Eq. (53). Both differential
equations must agree and this fact yields a condition for our unknown function 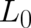 . Eq. (53)
also guarantees that the original constraint (55) is fulfilled. In this way we are able to ’transform’
the original variational condition for
. Eq. (53)
also guarantees that the original constraint (55) is fulfilled. In this way we are able to ’transform’
the original variational condition for 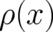 in a condition for
in a condition for 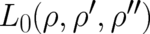 . In the
next section this condition will be used to calculate
. In the
next section this condition will be used to calculate 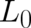 and to recover the form of the Fisher
and to recover the form of the Fisher
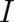 .
.
It should be mentioned that Eq. (58) has been used many times in the last eighty years to derive
Schrödinger’s equation from the Hamilton-Jacobi equation. The first and most important of these works is
Schrödinger’s ”‘Erste Mitteilung”’ [39]. In all of these papers 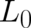 is not treated as an unknown function but
as a given function, constructed with the help of the following procedure. First, a transformation from the
variable
is not treated as an unknown function but
as a given function, constructed with the help of the following procedure. First, a transformation from the
variable 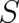 to a complex variable
to a complex variable ![ψ ′ = exp [iS ∕ ℏ ]](soqweb493x.png) is performed. Secondly, a new variable
is performed. Secondly, a new variable 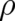 is
introduced by means of the formal replacement
is
introduced by means of the formal replacement 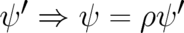 . This creates a new term in the
Lagrangian, which has exactly the form required to create quantum mechanics. More details on the
physical motivations underlying this replacement procedure may be found in a paper by Lee and
Zhu [29]. It is interesting to note that the same formal replacement may be used to perform the
transition from the London theory of superconductivity to the Ginzburg-Landau theory [25]. There, the
necessity to introduce a new variable is obvious, in contrast to the present much more intricate
situation.
. This creates a new term in the
Lagrangian, which has exactly the form required to create quantum mechanics. More details on the
physical motivations underlying this replacement procedure may be found in a paper by Lee and
Zhu [29]. It is interesting to note that the same formal replacement may be used to perform the
transition from the London theory of superconductivity to the Ginzburg-Landau theory [25]. There, the
necessity to introduce a new variable is obvious, in contrast to the present much more intricate
situation.