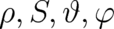 . The first of these is the continuity equation (56), which is given,
in terms of the present variables, by
. The first of these is the continuity equation (56), which is given,
in terms of the present variables, by
Let us summarize at this point what has been achieved so far. We have four coupled differential equations for
our dynamic field variables 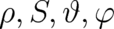 . The first of these is the continuity equation (56), which is given,
in terms of the present variables, by
. The first of these is the continuity equation (56), which is given,
in terms of the present variables, by
![∂ ρ ∂ ρ ∂ S e
-----+ ------[----(-------- --Aˆ )] = 0.
j
∂ t ∂ xl m ∂ xj c](stader360x.png) | (80) |
The three other differential equations, the evolution equations (73), (74) and the generalized Hamilton-Jacobi
equation (79), do not yet possess a definite mathematical form. They contain four unknown functions
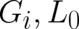 which are constrained, but not determined, by (75), (78).
which are constrained, but not determined, by (75), (78).
The simplest choice, from a formal point of view, is 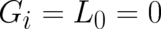 . In this limit the present theory
agrees with Schiller’s field-theoretic (Hamilton-Jacobi) version, see [60], of the equations of motion of a classical
dipole. This is a classical (statistical) theory despite the fact that it contains [see (63)] a number
. In this limit the present theory
agrees with Schiller’s field-theoretic (Hamilton-Jacobi) version, see [60], of the equations of motion of a classical
dipole. This is a classical (statistical) theory despite the fact that it contains [see (63)] a number 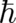 . But this
classical theory is not realized in nature; at least not in the microscopic domain. The reason is that the simplest
choice from a formal point of view is not the simplest choice from a physical point of view. The postulate of
maximal simplicity (Ockham’s razor) implies equal probabilities and the principle of maximal entropy
in classical statistical physics. A similar principle which is able to ’explain’ the nonexistence of
classical physics (in the microscopic domain) is the principle of minimal Fisher information [17]. The
relation between the two (classical and quantum-mechanical) principles has been discussed in detail in
I.
. But this
classical theory is not realized in nature; at least not in the microscopic domain. The reason is that the simplest
choice from a formal point of view is not the simplest choice from a physical point of view. The postulate of
maximal simplicity (Ockham’s razor) implies equal probabilities and the principle of maximal entropy
in classical statistical physics. A similar principle which is able to ’explain’ the nonexistence of
classical physics (in the microscopic domain) is the principle of minimal Fisher information [17]. The
relation between the two (classical and quantum-mechanical) principles has been discussed in detail in
I.
The mathematical formulation of the principle of minimal Fisher information for the present problem requires a
generalization, as compared to I, because we have now several fields with coupled time-evolution equations. As a
consequence, the spatial integral (spatial average) over  in the variational problem (44)
should be replaced by a space-time integral, and the variation should be performed with respect to all four
variables. The problem can be written in the form
in the variational problem (44)
should be replaced by a space-time integral, and the variation should be performed with respect to all four
variables. The problem can be written in the form
 is a shorthand notation for the equations (80), (79), (74) (73). Eqs. (81), (82) require
that the four Euler-Lagrange equations of the variational problem (81) agree with the differential
equations (82). This imposes conditions for the unknown functions
is a shorthand notation for the equations (80), (79), (74) (73). Eqs. (81), (82) require
that the four Euler-Lagrange equations of the variational problem (81) agree with the differential
equations (82). This imposes conditions for the unknown functions  . If the solutions of (81), (82)
for
. If the solutions of (81), (82)
for 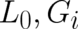 are inserted in the variational problem (81), the four relations (82) become redundant and
are inserted in the variational problem (81), the four relations (82) become redundant and
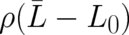 becomes the Lagrangian density of our problem. Thus, Eqs. (81) and (82) represent a
method to construct a Lagrangian.
becomes the Lagrangian density of our problem. Thus, Eqs. (81) and (82) represent a
method to construct a Lagrangian.
We assume a functional form 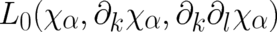 , where
, where 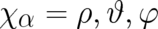 . This
means
. This
means 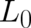 does not possess an explicit
does not possess an explicit 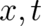 -dependence and does not depend on
-dependence and does not depend on 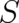 (this would lead to
a modification of the continuity equation). We further assume that
(this would lead to
a modification of the continuity equation). We further assume that 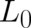 does not depend on time-derivatives
of
does not depend on time-derivatives
of 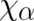 (the basic structure of the time-evolution equations should not be affected) and on spatial derivatives
higher than second order. These second order derivatives must be taken into account but should not give
contributions to the variational equations (a more detailed discussion of the last point has been given in
I).
(the basic structure of the time-evolution equations should not be affected) and on spatial derivatives
higher than second order. These second order derivatives must be taken into account but should not give
contributions to the variational equations (a more detailed discussion of the last point has been given in
I).
The variation with respect to 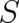 reproduces the continuity equation which is unimportant for the
determination of
reproduces the continuity equation which is unimportant for the
determination of 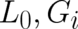 . Performing the variation with respect to
. Performing the variation with respect to 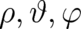 and taking the
corresponding conditions (79), (74) (73) into account leads to the following differential equations for
and taking the
corresponding conditions (79), (74) (73) into account leads to the following differential equations for
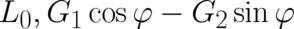 and
and 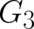 ,
,
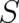 does not occur in (83)-(85) in agreement with our assumptions about the form of
does not occur in (83)-(85) in agreement with our assumptions about the form of 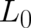 . It is
easy to see that a proper solution (with vanishing variational contributions from the second order derivatives)
of (83)-(85) is given by A new adjustable parameter appears on the r.h.s of (86)- (88) which has been identified with
. It is
easy to see that a proper solution (with vanishing variational contributions from the second order derivatives)
of (83)-(85) is given by A new adjustable parameter appears on the r.h.s of (86)- (88) which has been identified with 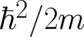 ,
where
,
where 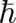 is again Planck’s constant. This second
is again Planck’s constant. This second 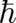 is related to the quantum-mechanical principle of
maximal disorder. It is in the present approach not related in any obvious way to the previous ”classical”
is related to the quantum-mechanical principle of
maximal disorder. It is in the present approach not related in any obvious way to the previous ”classical” 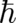 which denotes the amplitude of a rotation; compare, however, the alternative derivation of spin in
section 8.
which denotes the amplitude of a rotation; compare, however, the alternative derivation of spin in
section 8.
The solutions for 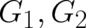 may be obtained with the help of the second condition (
may be obtained with the help of the second condition (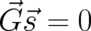 ) listed
in Eq. (75). The result may be written in the form
) listed
in Eq. (75). The result may be written in the form
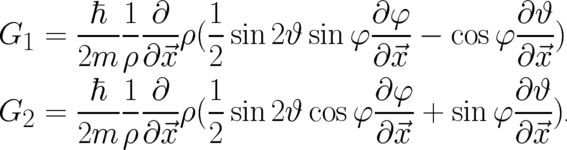 | (89) |
Eqs. (88) and (89) show that the first condition listed in (75) is also satisfied. The last condition is also fulfilled:
 can be written as
can be written as 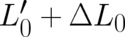 , where
, where
![2 ( )2 ( )2 2
ℏ ∂ φ ∂ ϑ ℏ 1 ∂ ∂ √ --
L ′ = - ------[ sin2 ϑ ----- - ----- ], ΔL = ------√-------------- ρ,
0 8m ∂ ⃗x ∂ ⃗x 0 2m ρ ∂ ⃗x ∂ ⃗x](stader395x.png) | (90) |
and 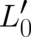 fulfills (78). We see that
fulfills (78). We see that 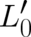 is a quantum-mechanical contribution to the rotational motion
while
is a quantum-mechanical contribution to the rotational motion
while 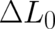 is related to the probability density of the ensemble (as could have been guessed
considering the mathematical form of these terms). The last term is the same as in the spinless case
[see (51)].
is related to the probability density of the ensemble (as could have been guessed
considering the mathematical form of these terms). The last term is the same as in the spinless case
[see (51)].
The remaining task is to show that the above solution for 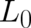 does indeed lead to a (appropriately
generalized) Fisher functional. This can be done in several ways. The simplest is to use the following result due
to [54]:
does indeed lead to a (appropriately
generalized) Fisher functional. This can be done in several ways. The simplest is to use the following result due
to [54]:
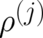 represent the probability that a particle is at space-time point
represent the probability that a particle is at space-time point 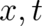 and
and 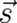 points
into direction
points
into direction 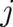 . Inserting (86) the validity of (91) may easily be verified. The r.h.s. of Eq. (91) shows that
the averaged value of
. Inserting (86) the validity of (91) may easily be verified. The r.h.s. of Eq. (91) shows that
the averaged value of 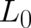 represents indeed a Fisher functional, which completes our calculation of the
’quantum terms’
represents indeed a Fisher functional, which completes our calculation of the
’quantum terms’ 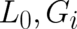 .
.
Summarizing, our assumption, that under certain external conditions four state variables instead of two may be
required, led to a nontrivial result, namely the four coupled differential equations (80), (79), (74), (73) with
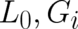 given by (86), (89), (88). The external condition which stimulates this splitting is
given by a gauge field; the most important case is a magnetic field
given by (86), (89), (88). The external condition which stimulates this splitting is
given by a gauge field; the most important case is a magnetic field 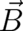 but other possibilities do
exist (see below). These four differential equations are equivalent to the much simpler differential
equation
but other possibilities do
exist (see below). These four differential equations are equivalent to the much simpler differential
equation
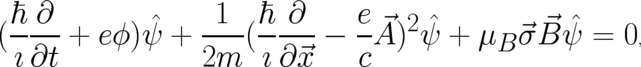 | (93) |
which is linear in the complex-valued two-component state variable 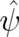 and is referred to as Pauli equation (the
components of the vector
and is referred to as Pauli equation (the
components of the vector 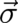 are the three Pauli matrices and
are the three Pauli matrices and 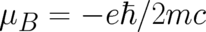 ). To see the
equivalence one writes, see [65], [26],
). To see the
equivalence one writes, see [65], [26],
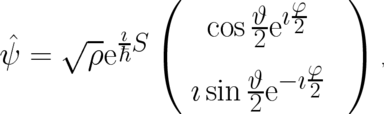 | (94) |
and evaluates the real and imaginary parts of the two scalar equations (93). This leads to the four differential equations (80), (79), (74) (73) and completes the present spin theory.
In terms of the real-valued functions 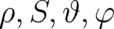 the quantum-mechanical solutions (86), (88), (89) for
the quantum-mechanical solutions (86), (88), (89) for
 look complicated in comparison to the classical solutions
look complicated in comparison to the classical solutions 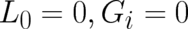 . In terms
of the variable
. In terms
of the variable 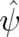 the situation changes to the contrary: The quantum-mechanical equation becomes simple
(linear) and the classical equation, which has been derived by [60], becomes complicated (nonlinear). The
simplicity of the underlying physical principle (principle of maximal disorder) leads to a simple mathematical
representation of the final basic equation (if a complex-valued state function is introduced). One may also say
that the linearity of the equations is a consequence of this principle of maximal disorder. This is the deeper
reason why it has been possible, see [32], to derive Schrödinger’s equation from a set of assumptions including
linearity.
the situation changes to the contrary: The quantum-mechanical equation becomes simple
(linear) and the classical equation, which has been derived by [60], becomes complicated (nonlinear). The
simplicity of the underlying physical principle (principle of maximal disorder) leads to a simple mathematical
representation of the final basic equation (if a complex-valued state function is introduced). One may also say
that the linearity of the equations is a consequence of this principle of maximal disorder. This is the deeper
reason why it has been possible, see [32], to derive Schrödinger’s equation from a set of assumptions including
linearity.
Besides the Pauli equation we found, as a second important result of our spin calculation, that the following local force is compatible with the statistical constraint:
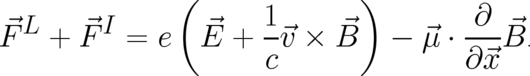 | (95) |
Here, the velocity field 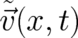 and the magnetic moment field
and the magnetic moment field 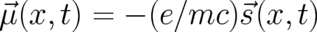 have been replaced by corresponding particle quantities
have been replaced by corresponding particle quantities 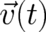 and
and 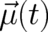 ; the dot denotes the inner
product between
; the dot denotes the inner
product between 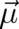 and
and 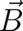 . The first force in (95), the Lorentz force, has been derived here from first
principles without any additional assumptions. The same cannot be said about the second force which takes this
particular form as a consequence of some additional assumptions concerning the form of the ’internal
force’
. The first force in (95), the Lorentz force, has been derived here from first
principles without any additional assumptions. The same cannot be said about the second force which takes this
particular form as a consequence of some additional assumptions concerning the form of the ’internal
force’ 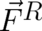 [see (71)]. In particular, the field appearing in
[see (71)]. In particular, the field appearing in 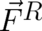 was arbitrary as well as the
proportionality constant (g-factor of the electron) and had to be adjusted by hand. It is well-known that in a
relativistic treatment the spin term appears automatically if the potentials are introduced. Interestingly,
this unity is not restricted to the relativistic regime. Following [5] and [19] we report in the next
section an alternative (non-relativistic) derivation of spin, which does not contain any arbitrary
fields or constants - but is unable to yield the expression (95) for the macroscopic electromagnetic
forces.
was arbitrary as well as the
proportionality constant (g-factor of the electron) and had to be adjusted by hand. It is well-known that in a
relativistic treatment the spin term appears automatically if the potentials are introduced. Interestingly,
this unity is not restricted to the relativistic regime. Following [5] and [19] we report in the next
section an alternative (non-relativistic) derivation of spin, which does not contain any arbitrary
fields or constants - but is unable to yield the expression (95) for the macroscopic electromagnetic
forces.
In the present treatment spin has been introduced as a property of an ensemble and not of individual particles.
Similar views may be found in the literature, see [49]. Of course, it is difficult to imagine the properties of an
ensemble as being completely independent from the properties of the particles it is made from. The question
whether or not a property ’spin’ can be ascribed to single particles is a subtle one. Formally, we could assign a
probability of being in a state 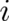 (
(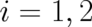 ) to a particle just as we assign a probability for being at a
position
) to a particle just as we assign a probability for being at a
position 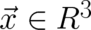 . But contrary to position, no classical meaning - and no classical measuring device - can
be associated with the discrete degree of freedom
. But contrary to position, no classical meaning - and no classical measuring device - can
be associated with the discrete degree of freedom 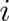 . Experimentally, the measurement of the ’spin of a
single electron’ is - in contrast to the measurement of its position - a notoriously difficult task. Such
experiments, and a number of other interesting questions related to spin, have been discussed by
[46].
. Experimentally, the measurement of the ’spin of a
single electron’ is - in contrast to the measurement of its position - a notoriously difficult task. Such
experiments, and a number of other interesting questions related to spin, have been discussed by
[46].