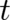 . Inserting (11) into (8),(9) leads to two equations. The first is the
continuity equation which takes the same form (13) as before. The second is the QHJ, which takes the
form
. Inserting (11) into (8),(9) leads to two equations. The first is the
continuity equation which takes the same form (13) as before. The second is the QHJ, which takes the
form
In QT, the coupling term in QHJ [see (9)] prevents a deterministic limit of the kind found for the PHJ. To see
this, we start from the assumption that a quantum mechanical system exists which admits a solution of the
form (11) for arbitrary 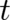 . Inserting (11) into (8),(9) leads to two equations. The first is the
continuity equation which takes the same form (13) as before. The second is the QHJ, which takes the
form
. Inserting (11) into (8),(9) leads to two equations. The first is the
continuity equation which takes the same form (13) as before. The second is the QHJ, which takes the
form
![( )
( )2 ( )2 { 3 }
∂ S 1 ∑ ∂ S 1 ℏ ∑
-----+ ------ ------- +V + ------ --- 3 ϵ - [x - r (t )]2 = 0.
∂ t 2m ∂ x 2m ϵ ( k k )
k
k k=1](climit107x.png) | (22) |
Eq. (22) shows that the coupling term diverges (for finite 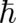 ) in the limit
) in the limit 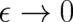 . Consequently, there is
no reason to expect, that the second derivative of
. Consequently, there is
no reason to expect, that the second derivative of 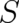 with respect to
with respect to 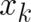 [see Eq. (13)] is regular at
[see Eq. (13)] is regular at
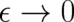 and that a delta-function-like
and that a delta-function-like 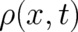 , as given by Eq. (11), can be a solution of (8), (9).
Thus, the deterministic limit of QT (if it exists) cannot be obtained in the same way as in the
PHJ.
, as given by Eq. (11), can be a solution of (8), (9).
Thus, the deterministic limit of QT (if it exists) cannot be obtained in the same way as in the
PHJ.
We next consider several concrete solutions of QT which lead to probability densities ’similar’ to (11). As a first
example we consider an ensemble of free particles which are distributed at 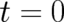 according to a
probability density (11) centered at
according to a
probability density (11) centered at 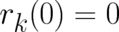 [set
[set 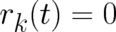 in (11)]. The initial
value for
in (11)]. The initial
value for 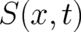 is given by
is given by 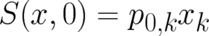 , i.e.
, i.e. 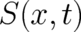 fulfills at
fulfills at
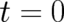 the ’deterministic’ relation (20). These initial values describe for small
the ’deterministic’ relation (20). These initial values describe for small 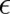 a localized,
classical particle in the sense that there is no uncertainty with respect to position or momentum. A
calculation found in many textbooks leads to the following solution of Schrödinger’s equation for
a localized,
classical particle in the sense that there is no uncertainty with respect to position or momentum. A
calculation found in many textbooks leads to the following solution of Schrödinger’s equation for 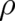 :
:
![( )
( ) 3- { 3 }
1 2 1 ∑ 2
ρ (x, t) = ---------- exp - -------- [x - r (t) ] ,
πA (t ) ( A (t) k k )
k=1](climit123x.png) | (23) |
where 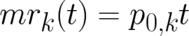 and
and ![A (t ) = A (t ) = ϵ [1 + ( ℏ ∕ ϵ)2 (t ∕m )2 ]
f](climit125x.png) .
We see from Eq. (23) that the peak of
.
We see from Eq. (23) that the peak of 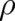 moves in agreement with NM, but the width of the wave
packet increases with increasing time as well as with decreasing
moves in agreement with NM, but the width of the wave
packet increases with increasing time as well as with decreasing 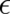 . A complete localization can
only be achieved at
. A complete localization can
only be achieved at 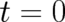 . At later times the quantum uncertainty, due to the finite
. At later times the quantum uncertainty, due to the finite 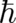 ,
dominates the behavior of the ensemble completely, despite our choice of ’deterministic’ initial
conditions.
,
dominates the behavior of the ensemble completely, despite our choice of ’deterministic’ initial
conditions.
As a second example, we consider an ensemble of particles moving in a harmonic oscillator potential
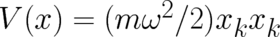 using exactly the same initial conditions as in the above example of
force-free motion. The result for
using exactly the same initial conditions as in the above example of
force-free motion. The result for 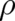 takes the same form (23) as for the force free ensemble, but with
takes the same form (23) as for the force free ensemble, but with
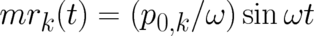 and
and
![[ ]
( )2
2 1 ℏ 2
A (t ) = A (t ) = ϵ cos ωt + ---------- --- sin ωt .
h m2 ω2 ϵ](climit133x.png) | (24) |
The width 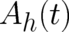 increases again with decreasing
increases again with decreasing 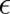 and prevents again a deterministic limit. We
mention, without going into details [23], that a third example showing the same behavior may be found, namely
an ensemble of particles moving under the influence of a constant force.
and prevents again a deterministic limit. We
mention, without going into details [23], that a third example showing the same behavior may be found, namely
an ensemble of particles moving under the influence of a constant force.
The three examples considered in this section correspond to three potentials proportional to 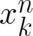 , where
, where
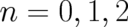 . For these potentials the expectation values of the corresponding forces fulfill the relation
. For these potentials the expectation values of the corresponding forces fulfill the relation
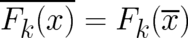 . Therefore, equations of motions for
. Therefore, equations of motions for 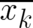 and
and 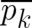 exist as a consequence of
Ehrenfest’s theorem. Despite of these classical features, even these ’optimal’ states do not permit a
deterministic limit of QT. We conclude, in agreement with common wisdom, that this limit does not
exist.
exist as a consequence of
Ehrenfest’s theorem. Despite of these classical features, even these ’optimal’ states do not permit a
deterministic limit of QT. We conclude, in agreement with common wisdom, that this limit does not
exist.