4 The ’deterministic limit’ of the ’standard limit’ of quantum theory
The deterministic limit of the classical-limit PHJ of QT is of considerable interest for the present problem,
despite the fact that the PHJ does no longer contain 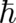 . Existence of a deterministic limit implies that
. Existence of a deterministic limit implies that
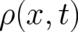 takes the form of a delta-function peaked at trajectory coordinates
takes the form of a delta-function peaked at trajectory coordinates 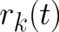 [which, hopefully,
should then be solutions of the classical equations (2)]. Thus, adopting a standard formula, we may write
[which, hopefully,
should then be solutions of the classical equations (2)]. Thus, adopting a standard formula, we may write
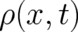 as an analytic function
as an analytic function
![( )
( ) 3-
2 { ∑ 3 }
-1-- 1- 2
ρ ϵ(x, t) = exp - [xk - rk (t )] ,
π ϵ ( ϵ )
k=1](climit69x.png) | (11) |
which represents 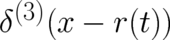 under the integral sign in the limit
under the integral sign in the limit 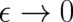 ,
,
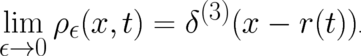 | (12) |
In order to check whether or not this deterministic representation of 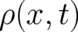 is compatible with the basic
equations of PHJ, we insert the Ansatz (11) into the continuity equation (8) and calculate the derivatives. After
some rearrangement (8) takes the form [18]
is compatible with the basic
equations of PHJ, we insert the Ansatz (11) into the continuity equation (8) and calculate the derivatives. After
some rearrangement (8) takes the form [18]
![{ ( ) }
∂ S (x, t ) ϵ ∂ ∂
------------- ----------------
ρ ϵ(x, t) [xk - rk (t ) ] pk (t ) - + S = 0,
∂ xk 2 ∂ xk ∂ xk](climit74x.png) | (13) |
where 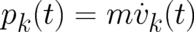 . At this point we recall that in the PHJ a momentum field
. At this point we recall that in the PHJ a momentum field
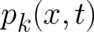 , defined by
, defined by
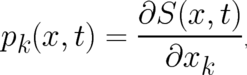 | (14) |
exists. The trajectory momentum 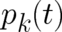 should be clearly distinguished from this field momentum
should be clearly distinguished from this field momentum
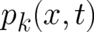 .
.
In the limit 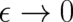 ,
, 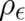 becomes a distribution and both sides of Eq. (13) have to be integrated over
three-dimensional space in order to obtain a mathematically well-defined expression. The first term in the
bracket vanishes as a consequence of the term
becomes a distribution and both sides of Eq. (13) have to be integrated over
three-dimensional space in order to obtain a mathematically well-defined expression. The first term in the
bracket vanishes as a consequence of the term 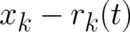 (at this point we start to disagree with
Ref [18]). The second term vanishes too for
(at this point we start to disagree with
Ref [18]). The second term vanishes too for 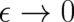 provided the second derivative of
provided the second derivative of 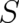 is regular at
is regular at
 . But this can safely be assumed since the equation for
. But this can safely be assumed since the equation for  does not contain
does not contain 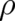 .
We conclude that the singular (deterministic) Ansatz (11) is a valid solution of PHJ for arbitrary
.
We conclude that the singular (deterministic) Ansatz (11) is a valid solution of PHJ for arbitrary
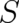 .
.
The present theory is incomplete since differential equations for the particle trajectories 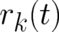 have still to
be found. Generally, two conditions must be fulfilled in order to define particle coordinates in a probabilistic
theory, namely (i) the limit of ’sharp’ (deterministic) probability distributions must be a valid solution, and (ii)
an evolution law for the time-dependent expectation values must exist. We have just shown that the first (more
critical) condition is fulfilled; Ehrenfest-like relations corresponding to the second condition exist in almost
all statistical theories. For the PHJ these take exactly the same form as in QT, namely [14, 12]
have still to
be found. Generally, two conditions must be fulfilled in order to define particle coordinates in a probabilistic
theory, namely (i) the limit of ’sharp’ (deterministic) probability distributions must be a valid solution, and (ii)
an evolution law for the time-dependent expectation values must exist. We have just shown that the first (more
critical) condition is fulfilled; Ehrenfest-like relations corresponding to the second condition exist in almost
all statistical theories. For the PHJ these take exactly the same form as in QT, namely [14, 12]
where average values such as 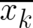 are defined according to the standard expression
are defined according to the standard expression
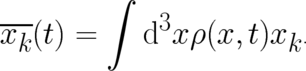 | (17) |
From (15) and the continuity equation (8) we obtain the following useful relation
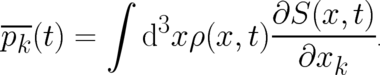 | (18) |
Since we have shown that the deterministic limit for  is a valid solution of PHJ, we may now use Eq. (12)
and obtain in the limit
is a valid solution of PHJ, we may now use Eq. (12)
and obtain in the limit  the following identification of trajectory quantities,
the following identification of trajectory quantities,
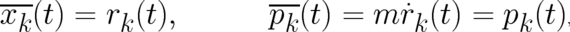 | (19) |
from the definitions of the expectation values. The differential relations connecting these quantities, follow from
Ehrenfest’s theorem and agree with the basic equations (2) of NM. A completely different type
of physical law has ’emerged’ from the field theoretic relations of the PHJ theory. Thus, classical
mechanics is, indeed, contained in PHJ as deterministic limit, in analogy to the second example of
section 2.
Eq. (18) takes in this limit the form
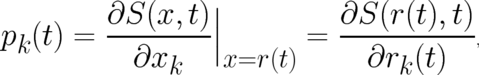 | (20) |
which provides an interesting link between a particle-variable and a field-variable. We expect for consistency that
this link admits a derivation of the equation for 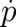 [see (2)] from the (field-theoretic) HJ-equation. This is
indeed the case. We calculate the derivative of the HJ equation (10) with respect to
[see (2)] from the (field-theoretic) HJ-equation. This is
indeed the case. We calculate the derivative of the HJ equation (10) with respect to 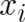 , change the order of
derivations with respect to
, change the order of
derivations with respect to 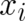 and
and 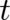 , and project the resulting relation on the trajectory points
, and project the resulting relation on the trajectory points
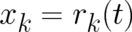 . This leads to the equation
. This leads to the equation
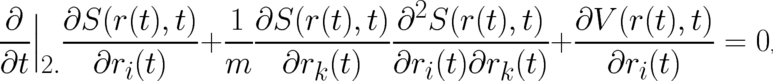 | (21) |
where the notation indicates that the time derivative operates on the second argument of 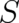 only. Using now
Eq. (20) and the definition of particle momentum we see that the first two terms of (21) agree exactly with the
(total) time-derivative of
only. Using now
Eq. (20) and the definition of particle momentum we see that the first two terms of (21) agree exactly with the
(total) time-derivative of 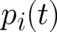 and (21) becomes the second Newton equation. This establishes the
connection between the PHJ equations and trajectory differential equations mentioned in section 3 and
completes our treatment of the deterministic limit of the PHJ theory. This derivation of NM seems to be new; it
is based on several interesting papers [19, 3, 13, 18, 8] reporting important steps in the right
direction.
and (21) becomes the second Newton equation. This establishes the
connection between the PHJ equations and trajectory differential equations mentioned in section 3 and
completes our treatment of the deterministic limit of the PHJ theory. This derivation of NM seems to be new; it
is based on several interesting papers [19, 3, 13, 18, 8] reporting important steps in the right
direction.
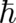 . Existence of a deterministic limit implies that
. Existence of a deterministic limit implies that
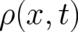 takes the form of a delta-function peaked at trajectory coordinates
takes the form of a delta-function peaked at trajectory coordinates 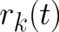 [which, hopefully,
should then be solutions of the classical equations (2)]. Thus, adopting a standard formula, we may write
[which, hopefully,
should then be solutions of the classical equations (2)]. Thus, adopting a standard formula, we may write
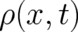 as an analytic function
as an analytic function
![( )
( ) 3-
2 { ∑ 3 }
-1-- 1- 2
ρ ϵ(x, t) = exp - [xk - rk (t )] ,
π ϵ ( ϵ )
k=1](climit69x.png)
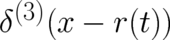 under the integral sign in the limit
under the integral sign in the limit  ,
,
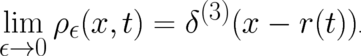
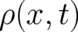 is compatible with the basic
equations of PHJ, we insert the Ansatz (
is compatible with the basic
equations of PHJ, we insert the Ansatz (![{ ( ) }
∂ S (x, t ) ϵ ∂ ∂
------------- ----------------
ρ ϵ(x, t) [xk - rk (t ) ] pk (t ) - + S = 0,
∂ xk 2 ∂ xk ∂ xk](climit74x.png)
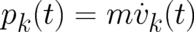 . At this point we recall that in the PHJ a momentum field
. At this point we recall that in the PHJ a momentum field
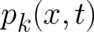 , defined by
, defined by
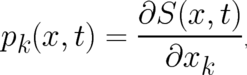
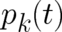 should be clearly distinguished from this field momentum
should be clearly distinguished from this field momentum
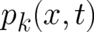 .
.
 ,
, 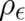 becomes a distribution and both sides of Eq. (
becomes a distribution and both sides of Eq. (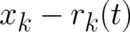 (at this point we start to disagree with
Ref
(at this point we start to disagree with
Ref 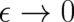 provided the second derivative of
provided the second derivative of 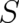 is regular at
is regular at
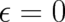 . But this can safely be assumed since the equation for
. But this can safely be assumed since the equation for 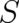 does not contain
does not contain 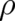 .
We conclude that the singular (deterministic) Ansatz (
.
We conclude that the singular (deterministic) Ansatz (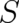 .
.
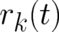 have still to
be found. Generally, two conditions must be fulfilled in order to define particle coordinates in a probabilistic
theory, namely (i) the limit of ’sharp’ (deterministic) probability distributions must be a valid solution, and (ii)
an evolution law for the time-dependent expectation values must exist. We have just shown that the first (more
critical) condition is fulfilled; Ehrenfest-like relations corresponding to the second condition exist in almost
all statistical theories. For the PHJ these take exactly the same form as in QT, namely
have still to
be found. Generally, two conditions must be fulfilled in order to define particle coordinates in a probabilistic
theory, namely (i) the limit of ’sharp’ (deterministic) probability distributions must be a valid solution, and (ii)
an evolution law for the time-dependent expectation values must exist. We have just shown that the first (more
critical) condition is fulfilled; Ehrenfest-like relations corresponding to the second condition exist in almost
all statistical theories. For the PHJ these take exactly the same form as in QT, namely 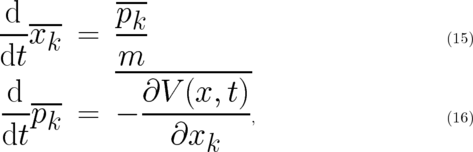
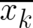 are defined according to the standard expression
are defined according to the standard expression
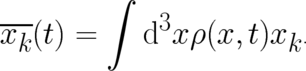
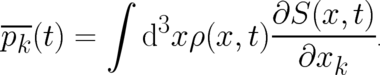
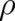 is a valid solution of PHJ, we may now use Eq. (
is a valid solution of PHJ, we may now use Eq. ( the following identification of trajectory quantities,
the following identification of trajectory quantities,
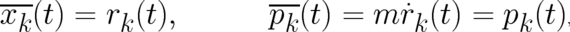
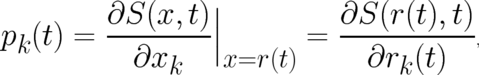
 [see (
[see ( , change the order of
derivations with respect to
, change the order of
derivations with respect to  and
and 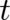 , and project the resulting relation on the trajectory points
, and project the resulting relation on the trajectory points
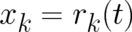 . This leads to the equation
. This leads to the equation
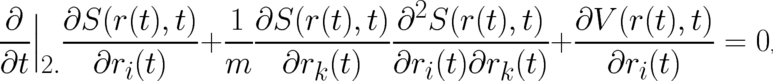
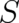 only. Using now
Eq. (
only. Using now
Eq. (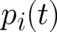 and (
and (