6 Energy conservation
In the last section [section (5)] we derived a second differential equation (26) for our dynamical variables 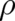 and
and 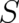 . This equation has some terms in common with the Hamilton-Jacobi equation of classical mechanics
but contains an unknown function
. This equation has some terms in common with the Hamilton-Jacobi equation of classical mechanics
but contains an unknown function 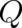 depending on
depending on 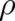 and
and 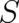 ; in principle it could also depend on
; in principle it could also depend on 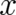 and
and 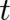 but this would contradict the homogeneity of space-time. We need further physical condition(s) to
determine those functions
but this would contradict the homogeneity of space-time. We need further physical condition(s) to
determine those functions 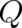 which are appropriate for a description of quantum mechanical reality or its
classical counterpart.
which are appropriate for a description of quantum mechanical reality or its
classical counterpart.
A rather obvious requirement is conservation of energy. In deterministic theories conservation laws - and in
particular the energy conservation law which will be considered exclusively here - are a logical consequence of the
basic equations; there is no need for separate postulates in this case. In statistical theories energy
conservation with regard to time-dependence of single events is of course meaningless. However, a
statistical analog of this conservation law may be formulated as follows: “The statistical average of
the random variable energy is time-independent”. In the present framework it is expressed by the
relation
![[ ]
∫ ∫
d ∞ p2 ∞
---- dpw (p, t) ------+ dx ρ (x, t )V (x ) = 0.
dt - ∞ 2m - ∞](soqweb224x.png) | (33) |
We will use the abbreviation 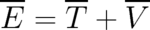 for the bracket where
for the bracket where 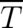 denotes the first and
denotes the first and 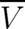 denotes the second term respectively. Here, in contrast to the deterministic case, the fundamental laws
[namely (2), (3), (7)] do not guarantee the validity of (33). It has to be implemented as a separate
statistical condition. In fact, Eq. (33) is very simple and convincing; it seems reasonable to keep only
those statistical theories which obey the statistical version of the fundamental energy conservation
law.
denotes the second term respectively. Here, in contrast to the deterministic case, the fundamental laws
[namely (2), (3), (7)] do not guarantee the validity of (33). It has to be implemented as a separate
statistical condition. In fact, Eq. (33) is very simple and convincing; it seems reasonable to keep only
those statistical theories which obey the statistical version of the fundamental energy conservation
law.
In writing down Eq. (33) a second tacit assumption, besides the postulate of energy conservation, has been
made, namely that a standard random variable “kinetic energy” exists; this assumption has already been
formulated and partly justified in the last section. This means, in particular, that the probability
density 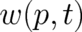 , which has been introduced in the statistical conditions (2), (3) to obtain
the expectation value of
, which has been introduced in the statistical conditions (2), (3) to obtain
the expectation value of 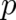 may also be used to calculate the expectation value of
may also be used to calculate the expectation value of 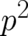 . This
second assumption is - like the requirement of energy conservation - not a consequence of the basic
equations (26), (7). The latter may be used to calculate the probability density
. This
second assumption is - like the requirement of energy conservation - not a consequence of the basic
equations (26), (7). The latter may be used to calculate the probability density 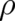 but says nothing about the
calculation of expectation values of
but says nothing about the
calculation of expectation values of 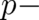 dependent quantities. Thus, Eq. (33) is an additional
assumption, as may also be seen by the fact that two unknown functions, namely
dependent quantities. Thus, Eq. (33) is an additional
assumption, as may also be seen by the fact that two unknown functions, namely 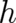 and
and 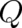 occur
in (33).
occur
in (33).
Eq. (33) defines a relation between 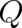 and
and 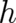 . More precisely, we consider variables
. More precisely, we consider variables 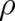 and
and 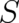 which are solutions of the two basic equations (26) and (7), where
which are solutions of the two basic equations (26) and (7), where 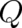 may be an arbitrary
function of
may be an arbitrary
function of 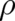 ,
, 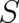 . Using these solutions we look which (differential) relations between
. Using these solutions we look which (differential) relations between 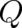 and
and
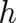 are compatible with the requirement (33). Postulating the validity of (33) implies certain
relations (yet to be found in explicit form) between the equations determining the probabilities
and the equations defining the expectation values of
are compatible with the requirement (33). Postulating the validity of (33) implies certain
relations (yet to be found in explicit form) between the equations determining the probabilities
and the equations defining the expectation values of 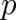 -dependent quantities (like the kinetic
energy).
-dependent quantities (like the kinetic
energy).
In a first step we rewrite the statistical average of 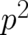 in (33) using (21). The result is
in (33) using (21). The result is
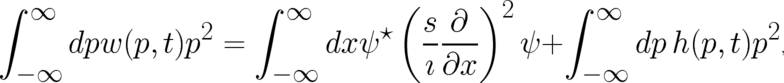 | (34) |
as may be verified with the help of (20). Using (34), transforming to 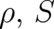 , and performing an integration
by parts, the first term of (33) takes the form
, and performing an integration
by parts, the first term of (33) takes the form
![--- ∫ { [ ( ) ( ) ]
∞ 2 2 2 2 2
d-T-- --1--- -s---- ∂-ρ-- s--- ∂--ρ--- ∂-S-- ∂-ρ--
= dx 2 - 2 +
dt 2m - ∞ 4ρ ∂ x 2 ρ ∂ x ∂ x ∂ t
}
[ 2 ] ∫ ∞ 2
∂ ρ ∂ S ∂ S ∂ S ∂ h (p, t) p
- 2 ---------- + ρ ------- ----- + dp ------------------.
∂ x ∂ x ∂ x2 ∂ t ∂ t 2m
- ∞](soqweb248x.png) | (35) |
If we add the time derivative of 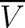 to (35) we obtain the time derivative of
to (35) we obtain the time derivative of 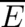 , as defined by the left hand
side of (33). In the integrand of the latter expression the following term occurs
, as defined by the left hand
side of (33). In the integrand of the latter expression the following term occurs
![[ ] [ ]
( )2 2
∂ S ∂ ρ ∂ ρ ∂ S ∂ S ∂ S
----- + 2mV ----- - 2 ---------- + ρ ------- ----- .
∂ x ∂ t ∂ x ∂ x 2 ∂ t
∂ x](soqweb251x.png) | (36) |
The two brackets in (36) may be rewritten with the help of (7) and (26). Then, the term (36) takes the much
simpler form
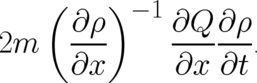 | (37) |
Using (35) and (37) we find that the statistical condition (33) implies the following integral relation between
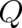 and
and 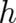 .
.
![∫ [ ( ) √ --]
∞ ∂ ρ - 1 ∂ Q s2 1 ∂ 2 ρ ∂ ρ
----- ------ --------------------- -----
dx - √ -- 2
- ∞ ∂ x ∂ x 2m ρ ∂ x ∂ t
∫
∞ ∂ h (p, t ) p2
+ dp -------------------= 0.
- ∞ ∂ t 2m](soqweb255x.png) | (38) |
Let us first investigate the classical solution. We may either insert the classical, “hybrid” solution (10) for
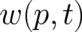 directly into Eq.(33) or insert
directly into Eq.(33) or insert 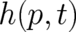 according to (21) with
according to (21) with 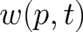 as given
by (10) in (38), to obtain
as given
by (10) in (38), to obtain
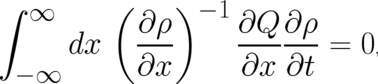 | (39) |
which implies 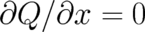 . Thus, the hybrid probability density (10) leads, as expected, to a
classical (the equation for
. Thus, the hybrid probability density (10) leads, as expected, to a
classical (the equation for 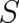 does not contain terms dependent on
does not contain terms dependent on 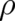 ) statistical theory, given by the
Hamilton-Jacobi equation and the continuity equation. These equations constitute the classical limit of quantum
mechanics which is a statistical theory (of type 2 according to the above classification) and not a deterministic
(type 1) theory like classical mechanics. This difference is very important and should be borne in mind. The
various ambiguities [27] one encounters in the conventional particle picture both in the transitions from
classical physics to quantum mechanics and back to classical physics, do not exist in the present
approach.
) statistical theory, given by the
Hamilton-Jacobi equation and the continuity equation. These equations constitute the classical limit of quantum
mechanics which is a statistical theory (of type 2 according to the above classification) and not a deterministic
(type 1) theory like classical mechanics. This difference is very important and should be borne in mind. The
various ambiguities [27] one encounters in the conventional particle picture both in the transitions from
classical physics to quantum mechanics and back to classical physics, do not exist in the present
approach.
If we insert the quantum-mechanical result (29) with properly adjusted constant in (38), we
obtain
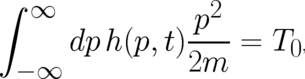 | (40) |
where 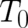 is an arbitrary time-independent constant. This constant reflects the possibility to fix a zero point
of a (kinetic energy) scale. An analogous arbitrary constant
is an arbitrary time-independent constant. This constant reflects the possibility to fix a zero point
of a (kinetic energy) scale. An analogous arbitrary constant 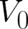 occurs for the potential energy. Since kinetic
energy occurs always (in all physically meaningful contexts) together with potential energy, the constant
occurs for the potential energy. Since kinetic
energy occurs always (in all physically meaningful contexts) together with potential energy, the constant 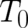 may be eliminated with the help of a properly adjusted
may be eliminated with the help of a properly adjusted 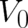 . Therefore, we see that - as far as the calculation
of the expectation value of the kinetic energy is concerned - it is allowed to set
. Therefore, we see that - as far as the calculation
of the expectation value of the kinetic energy is concerned - it is allowed to set 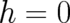 . Combined with
previous results, we see that
. Combined with
previous results, we see that 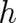 may be set equal to
may be set equal to  as far as the calculation of the expectation values of
as far as the calculation of the expectation values of
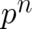 , for
, for 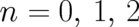 is concerned. These cases include all cases of practical importance. A universal
rule for the calculation of averages of arbitrary powers of
is concerned. These cases include all cases of practical importance. A universal
rule for the calculation of averages of arbitrary powers of 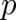 is not available in the present theory. The same is
true for arbitrary powers of
is not available in the present theory. The same is
true for arbitrary powers of 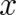 and
and 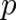 . Fortunately, this is not really a problem since the above
powers cover all cases of physical interest, as far as powers of
. Fortunately, this is not really a problem since the above
powers cover all cases of physical interest, as far as powers of 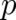 are concerned (combinations
of powers of
are concerned (combinations
of powers of 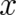 and
and 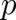 do not occur in the present theory and will be dealt with in a future
work).
do not occur in the present theory and will be dealt with in a future
work).
It is informative to compare the present theory with the corresponding situation in the established
formulations of quantum mechanics. In the conventional quantization procedure, which is ideologically
dominated by the structure of particle mechanics, it is postulated that all classical observables (arbitrary
functions of 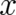 and
and 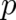 ) be represented by operators in Hilbert space. The explicit construction of these
operators runs into considerable difficulties [42] for all except the simplest combinations of
) be represented by operators in Hilbert space. The explicit construction of these
operators runs into considerable difficulties [42] for all except the simplest combinations of 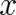 and
and 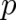 . But,
typically, this does not cause any real problems since all simple combinations (of physical interest) can be
represented in a unique way by corresponding operators. Thus, what is wrong - or rather ill-posed - is
obviously the postulate itself, which creates an artificial problem. This is one example, among several
others, for an artificial problem created by choosing the wrong (deterministic) starting point for
quantization.
. But,
typically, this does not cause any real problems since all simple combinations (of physical interest) can be
represented in a unique way by corresponding operators. Thus, what is wrong - or rather ill-posed - is
obviously the postulate itself, which creates an artificial problem. This is one example, among several
others, for an artificial problem created by choosing the wrong (deterministic) starting point for
quantization.
If we start from the r.h.s. of (38) and postulate 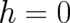 , then we obtain agreement with the standard
formalism of quantum mechanics, both with regard to the time evolution equation and the rules for calculating
expectation values of
, then we obtain agreement with the standard
formalism of quantum mechanics, both with regard to the time evolution equation and the rules for calculating
expectation values of 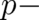 dependent quantities. Thus,
dependent quantities. Thus, 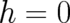 is a rather strong condition.
Unfortunately, there seems be no intuitive interpretation at all for this condition. It is even less
understandable than our previous formal postulate leading to Schrödinger’s equation, the requirement of a
complex state variable. Thus, while we gained in this section important insight in the relation between
energy conservation, time-evolution equation and rules for calculating expectation values, still other
methods are required if we want to derive quantum mechanics from a set of physically interpretable
postulates.
is a rather strong condition.
Unfortunately, there seems be no intuitive interpretation at all for this condition. It is even less
understandable than our previous formal postulate leading to Schrödinger’s equation, the requirement of a
complex state variable. Thus, while we gained in this section important insight in the relation between
energy conservation, time-evolution equation and rules for calculating expectation values, still other
methods are required if we want to derive quantum mechanics from a set of physically interpretable
postulates.
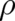 and
and 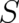 . This equation has some terms in common with the Hamilton-Jacobi equation of classical mechanics
but contains an unknown function
. This equation has some terms in common with the Hamilton-Jacobi equation of classical mechanics
but contains an unknown function 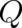 depending on
depending on 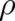 and
and 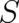 ; in principle it could also depend on
; in principle it could also depend on 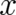 and
and 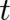 but this would contradict the homogeneity of space-time. We need further physical condition(s) to
determine those functions
but this would contradict the homogeneity of space-time. We need further physical condition(s) to
determine those functions 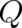 which are appropriate for a description of quantum mechanical reality or its
classical counterpart.
which are appropriate for a description of quantum mechanical reality or its
classical counterpart.
![[ ]
∫ ∫
d ∞ p2 ∞
---- dpw (p, t) ------+ dx ρ (x, t )V (x ) = 0.
dt - ∞ 2m - ∞](soqweb224x.png)
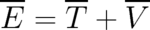 for the bracket where
for the bracket where 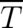 denotes the first and
denotes the first and 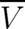 denotes the second term respectively. Here, in contrast to the deterministic case, the fundamental laws
[namely (
denotes the second term respectively. Here, in contrast to the deterministic case, the fundamental laws
[namely (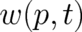 , which has been introduced in the statistical conditions (
, which has been introduced in the statistical conditions (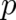 may also be used to calculate the expectation value of
may also be used to calculate the expectation value of 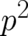 . This
second assumption is - like the requirement of energy conservation - not a consequence of the basic
equations (
. This
second assumption is - like the requirement of energy conservation - not a consequence of the basic
equations (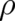 but says nothing about the
calculation of expectation values of
but says nothing about the
calculation of expectation values of 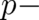 dependent quantities. Thus, Eq. (
dependent quantities. Thus, Eq. (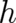 and
and 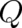 occur
in (
occur
in (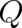 and
and 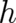 . More precisely, we consider variables
. More precisely, we consider variables 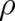 and
and 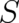 which are solutions of the two basic equations (
which are solutions of the two basic equations (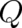 may be an arbitrary
function of
may be an arbitrary
function of 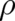 ,
, 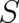 . Using these solutions we look which (differential) relations between
. Using these solutions we look which (differential) relations between 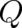 and
and
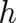 are compatible with the requirement (
are compatible with the requirement (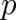 -dependent quantities (like the kinetic
energy).
-dependent quantities (like the kinetic
energy).
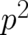 in (
in (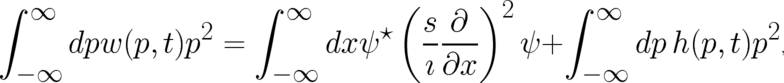
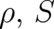 , and performing an integration
by parts, the first term of (
, and performing an integration
by parts, the first term of (![--- ∫ { [ ( ) ( ) ]
∞ 2 2 2 2 2
d-T-- --1--- -s---- ∂-ρ-- s--- ∂--ρ--- ∂-S-- ∂-ρ--
= dx 2 - 2 +
dt 2m - ∞ 4ρ ∂ x 2 ρ ∂ x ∂ x ∂ t
}
[ 2 ] ∫ ∞ 2
∂ ρ ∂ S ∂ S ∂ S ∂ h (p, t) p
- 2 ---------- + ρ ------- ----- + dp ------------------.
∂ x ∂ x ∂ x2 ∂ t ∂ t 2m
- ∞](soqweb248x.png)
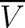 to (
to (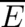 , as defined by the left hand
side of (
, as defined by the left hand
side of (![[ ] [ ]
( )2 2
∂ S ∂ ρ ∂ ρ ∂ S ∂ S ∂ S
----- + 2mV ----- - 2 ---------- + ρ ------- ----- .
∂ x ∂ t ∂ x ∂ x 2 ∂ t
∂ x](soqweb251x.png)
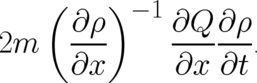
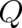 and
and 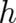 .
.
![∫ [ ( ) √ --]
∞ ∂ ρ - 1 ∂ Q s2 1 ∂ 2 ρ ∂ ρ
----- ------ --------------------- -----
dx - √ -- 2
- ∞ ∂ x ∂ x 2m ρ ∂ x ∂ t
∫
∞ ∂ h (p, t ) p2
+ dp -------------------= 0.
- ∞ ∂ t 2m](soqweb255x.png)
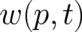 directly into Eq.(
directly into Eq.(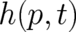 according to (
according to (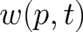 as given
by (
as given
by (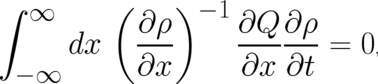
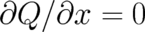 . Thus, the hybrid probability density (
. Thus, the hybrid probability density ( does not contain terms dependent on
does not contain terms dependent on  ) statistical theory, given by the
Hamilton-Jacobi equation and the continuity equation. These equations constitute the classical limit of quantum
mechanics which is a statistical theory (of type 2 according to the above classification) and not a deterministic
(type 1) theory like classical mechanics. This difference is very important and should be borne in mind. The
various ambiguities
) statistical theory, given by the
Hamilton-Jacobi equation and the continuity equation. These equations constitute the classical limit of quantum
mechanics which is a statistical theory (of type 2 according to the above classification) and not a deterministic
(type 1) theory like classical mechanics. This difference is very important and should be borne in mind. The
various ambiguities 
 is an arbitrary time-independent constant. This constant reflects the possibility to fix a zero point
of a (kinetic energy) scale. An analogous arbitrary constant
is an arbitrary time-independent constant. This constant reflects the possibility to fix a zero point
of a (kinetic energy) scale. An analogous arbitrary constant  occurs for the potential energy. Since kinetic
energy occurs always (in all physically meaningful contexts) together with potential energy, the constant
occurs for the potential energy. Since kinetic
energy occurs always (in all physically meaningful contexts) together with potential energy, the constant  may be eliminated with the help of a properly adjusted
may be eliminated with the help of a properly adjusted 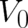 . Therefore, we see that - as far as the calculation
of the expectation value of the kinetic energy is concerned - it is allowed to set
. Therefore, we see that - as far as the calculation
of the expectation value of the kinetic energy is concerned - it is allowed to set 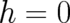 . Combined with
previous results, we see that
. Combined with
previous results, we see that 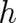 may be set equal to
may be set equal to  as far as the calculation of the expectation values of
as far as the calculation of the expectation values of
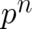 , for
, for 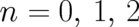 is concerned. These cases include all cases of practical importance. A universal
rule for the calculation of averages of arbitrary powers of
is concerned. These cases include all cases of practical importance. A universal
rule for the calculation of averages of arbitrary powers of 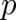 is not available in the present theory. The same is
true for arbitrary powers of
is not available in the present theory. The same is
true for arbitrary powers of 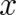 and
and 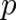 . Fortunately, this is not really a problem since the above
powers cover all cases of physical interest, as far as powers of
. Fortunately, this is not really a problem since the above
powers cover all cases of physical interest, as far as powers of 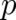 are concerned (combinations
of powers of
are concerned (combinations
of powers of 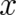 and
and 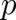 do not occur in the present theory and will be dealt with in a future
work).
do not occur in the present theory and will be dealt with in a future
work).
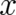 and
and 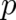 ) be represented by operators in Hilbert space. The explicit construction of these
operators runs into considerable difficulties
) be represented by operators in Hilbert space. The explicit construction of these
operators runs into considerable difficulties 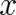 and
and 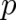 . But,
typically, this does not cause any real problems since all simple combinations (of physical interest) can be
represented in a unique way by corresponding operators. Thus, what is wrong - or rather ill-posed - is
obviously the postulate itself, which creates an artificial problem. This is one example, among several
others, for an artificial problem created by choosing the wrong (deterministic) starting point for
quantization.
. But,
typically, this does not cause any real problems since all simple combinations (of physical interest) can be
represented in a unique way by corresponding operators. Thus, what is wrong - or rather ill-posed - is
obviously the postulate itself, which creates an artificial problem. This is one example, among several
others, for an artificial problem created by choosing the wrong (deterministic) starting point for
quantization.
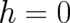 , then we obtain agreement with the standard
formalism of quantum mechanics, both with regard to the time evolution equation and the rules for calculating
expectation values of
, then we obtain agreement with the standard
formalism of quantum mechanics, both with regard to the time evolution equation and the rules for calculating
expectation values of 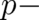 dependent quantities. Thus,
dependent quantities. Thus, 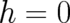 is a rather strong condition.
Unfortunately, there seems be no intuitive interpretation at all for this condition. It is even less
understandable than our previous formal postulate leading to Schrödinger’s equation, the requirement of a
complex state variable. Thus, while we gained in this section important insight in the relation between
energy conservation, time-evolution equation and rules for calculating expectation values, still other
methods are required if we want to derive quantum mechanics from a set of physically interpretable
postulates.
is a rather strong condition.
Unfortunately, there seems be no intuitive interpretation at all for this condition. It is even less
understandable than our previous formal postulate leading to Schrödinger’s equation, the requirement of a
complex state variable. Thus, while we gained in this section important insight in the relation between
energy conservation, time-evolution equation and rules for calculating expectation values, still other
methods are required if we want to derive quantum mechanics from a set of physically interpretable
postulates.