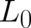
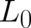
For a general 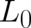 , the Euler-Lagrange equation belonging to the functional
, the Euler-Lagrange equation belonging to the functional ![C [ρ ]](soqweb498x.png) [see (58)]
depends on derivatives higher than second order since the integrand in (58) depends on
[see (58)]
depends on derivatives higher than second order since the integrand in (58) depends on 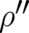 . This
is a problem, since according to the universal rule mentioned above all differential equations of
physics are formulated using derivatives not higher than second order. If we are to conform with this
general rule (and we would like to do so) then we should use a Lagrangian containing only first order
derivatives. But this would then again produce a conflict with Eq. (53) because the variational
procedure increases the order of the highest derivative by one. We postpone the resolution of this
conflict and proceed by calculating the Euler-Lagrange equations according to (58), which are given
by
. This
is a problem, since according to the universal rule mentioned above all differential equations of
physics are formulated using derivatives not higher than second order. If we are to conform with this
general rule (and we would like to do so) then we should use a Lagrangian containing only first order
derivatives. But this would then again produce a conflict with Eq. (53) because the variational
procedure increases the order of the highest derivative by one. We postpone the resolution of this
conflict and proceed by calculating the Euler-Lagrange equations according to (58), which are given
by
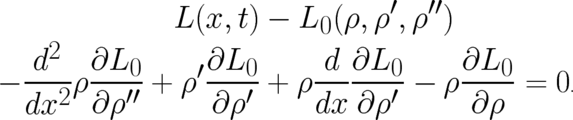 | (59) |
Using the second basic condition (53) we see that the first line of Eq. (59) vanishes and we obtain, introducing
the abbreviation 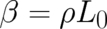 , the following partial differential equation for the determination of the
functional form of
, the following partial differential equation for the determination of the
functional form of 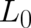 with respect to the variables
with respect to the variables 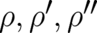 ,
,
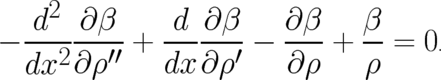 | (60) |
Expressing the derivatives of 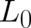 in terms of the derivatives of
in terms of the derivatives of 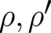 and
and 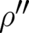 leads to a lengthy
relation which will not be written down here. Since
leads to a lengthy
relation which will not be written down here. Since 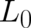 does not contain higher derivatives than
does not contain higher derivatives than 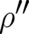 , the
sums of the coefficients of both the third and fourth derivatives of
, the
sums of the coefficients of both the third and fourth derivatives of 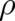 have to vanish. This implies that
have to vanish. This implies that 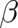 may be written in the form
may be written in the form
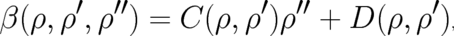 | (61) |
where 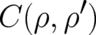 and
and 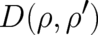 are solutions of
are solutions of
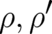 have to be found, instead of a single function of
have to be found, instead of a single function of 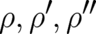 . Fortunately,
the solution we look for presents a term in a differential equation. This allows us to restrict our search to
relatively simple solutions of (62), (63). If the differential equation is intended to be comparable in complexity
to other fundamental laws of physics, then a polynomial form,
. Fortunately,
the solution we look for presents a term in a differential equation. This allows us to restrict our search to
relatively simple solutions of (62), (63). If the differential equation is intended to be comparable in complexity
to other fundamental laws of physics, then a polynomial form,
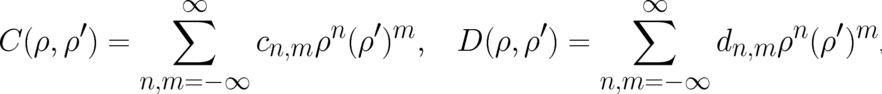 | (64) |
preferably with a finite number of terms, will be a sufficiently general Ansatz.
Eqs. (62) and (63) must of course hold for arbitrary 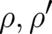 . Inserting the Ansatz (64), renaming indices
and comparing coefficients of equal powers of
. Inserting the Ansatz (64), renaming indices
and comparing coefficients of equal powers of 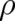 and
and 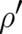 one obtains the relations
one obtains the relations
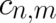 and
and 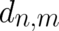 . These relations may be used to calculate those values of
. These relations may be used to calculate those values of 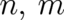 which allow for non-vanishing coefficients and to calculate the proportionality constants between these
coefficients; e.g. Eq. (65) may be used to express
which allow for non-vanishing coefficients and to calculate the proportionality constants between these
coefficients; e.g. Eq. (65) may be used to express 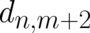 in terms of
in terms of 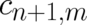 provided
provided
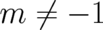 and
and 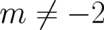 . One obtains the result that the general solution
. One obtains the result that the general solution 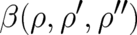 of (60) of polynomial form is given by (61), with where
of (60) of polynomial form is given by (61), with where 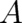 and
and 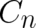 are arbitrary constants and the index set
are arbitrary constants and the index set 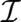 is given by
is given by
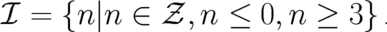 | (69) |
While the derivation of (67), (68) is straightforward but lengthy, the fact that (61), (67), (68) fulfills (60) may be verified easily.
At this point we are looking for further constraints in order to reduce the number of unknown constants.
The simplest (nontrivial) special case of (61), (67), (68) is 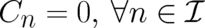 . The
corresponding solution for
. The
corresponding solution for 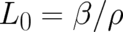 is given by
is given by 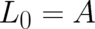 . However, a solution
given by a nonzero constant
. However, a solution
given by a nonzero constant 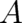 may be eliminated by adding a corresponding constant to the
potential in
may be eliminated by adding a corresponding constant to the
potential in 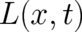 . Thus, this solution need not be taken into account and we may set
. Thus, this solution need not be taken into account and we may set
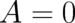 .
.
The ’next simplest’ solution, given by 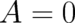 ,
, 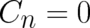 for all
for all 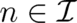 except
except
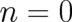 , takes the form
, takes the form
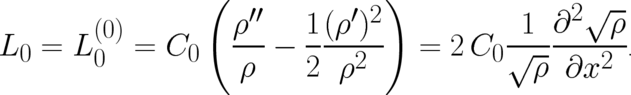 | (70) |
Let us also write down here, for later use, the solution given by 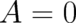 ,
, 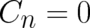 for all
for all
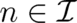 except
except 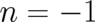 . It takes the form
. It takes the form
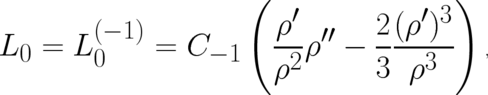 | (71) |
Comparison of the r.h.s. of Eq. (70) with Eq. (29) shows that the solution (70) leads to Schrödinger’s
equation (32). At this point the question arises why this particular solution has been realized by nature - and
not any other from the huge set of possible solutions. Eq. (70) consists of two parts. Let us consider the two
corresponding terms in 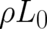 , which represent two contributions to the Lagrangian in Eq. (56).
The second of these terms agrees with the integrand of the Fisher functional (48). The first is
proportional to
, which represent two contributions to the Lagrangian in Eq. (56).
The second of these terms agrees with the integrand of the Fisher functional (48). The first is
proportional to 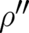 . This first term may be omitted in the Lagrangian (under the integral sign)
because it represents a boundary (or surface) term and gives no contribution to the Euler-Lagrange
equations [it must not be omitted in the final differential equation (53), where exactly the same
term reappears as a consequence of the differentiation of
. This first term may be omitted in the Lagrangian (under the integral sign)
because it represents a boundary (or surface) term and gives no contribution to the Euler-Lagrange
equations [it must not be omitted in the final differential equation (53), where exactly the same
term reappears as a consequence of the differentiation of  ]. Thus, integrating the contribution
]. Thus, integrating the contribution
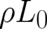 of the solution (70) to the Lagrangian yields exactly the Fisher functional. No other
solution with this property exists. Therefore, the reason why nature has chosen this particular
solution is basically the same as in classical statistics, namely the principle of maximal disorder -
but realized in a different (local) context and expressed in terms of a principle of minimal Fisher
information.
of the solution (70) to the Lagrangian yields exactly the Fisher functional. No other
solution with this property exists. Therefore, the reason why nature has chosen this particular
solution is basically the same as in classical statistics, namely the principle of maximal disorder -
but realized in a different (local) context and expressed in terms of a principle of minimal Fisher
information.
We see that the conflict mentioned at the beginning of this section does not exist for the quantum mechanical
solution (70). The reason is again that the term in 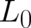 containing the second derivative
containing the second derivative 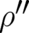 is of the form
of a total derivative and can, consequently, be neglected as far as its occurrence in the term
is of the form
of a total derivative and can, consequently, be neglected as far as its occurrence in the term 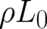 of the
Lagrangian is concerned. Generalizing this fact, we may formulate the following criterion for the absence of any
conflict: The terms in
of the
Lagrangian is concerned. Generalizing this fact, we may formulate the following criterion for the absence of any
conflict: The terms in 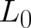 containing
containing 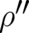 must not yield contributions to the variation, i. e. they must in
the present context take the form of total derivatives (for more general variational problems such terms are
called ”‘null Lagrangians”’ [13]).
must not yield contributions to the variation, i. e. they must in
the present context take the form of total derivatives (for more general variational problems such terms are
called ”‘null Lagrangians”’ [13]).
So far, in order to reduce the number of our integration constants, we used the criterion that the
corresponding term in the Lagrangian should agree with the form of Fishers functional. This ‘direct’
implementation of the principle of maximal disorder led to quantum mechanics. The absence of the above
mentioned conflict means that the theory may be formulated using a Lagrangian containing no derivatives higher
than first order. As is well known, this is a criterion universally realized in nature; a list of fundamental physical
laws obeying this criterion may e.g. be found in a paper by Frieden and Soffer [12]. Thus, it is convincing
although of a ’formal’ character. Let us apply this ’formal’ criterion as an alternative physical argument
to reduce the number of unknown coefficients the above solution. This criterion implies, that the
derivatives of 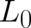 with respect to
with respect to 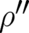 do not play any role, i.e. the solutions of (60) must also
obey
do not play any role, i.e. the solutions of (60) must also
obey
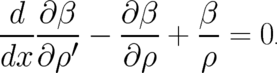 | (72) |
This implies that only those solutions of (60) are acceptable, which obey
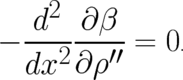 | (73) |
Using (61) and (67) it is easy to see that the solution (70) belonging to  is the only solution
compatible with the requirement (73) [as one would suspect it is also possible to derive (70) directly from (72)].
Thus the ’formal’ principle, that the Lagrangian contains no terms of order higher than one, leads to the same
result as the ’direct’ application of the principle of maximal disorder. The deep connection between statistical
criteria and the form of the kinetic energy terms in the fundamental laws of physics has been mentioned before
in the literature [11]. The present derivation sheds new light, from a different perspective, on this
connection.
is the only solution
compatible with the requirement (73) [as one would suspect it is also possible to derive (70) directly from (72)].
Thus the ’formal’ principle, that the Lagrangian contains no terms of order higher than one, leads to the same
result as the ’direct’ application of the principle of maximal disorder. The deep connection between statistical
criteria and the form of the kinetic energy terms in the fundamental laws of physics has been mentioned before
in the literature [11]. The present derivation sheds new light, from a different perspective, on this
connection.
Summarizing, the shape of our unknown function  has been found. The result for
has been found. The result for 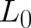 leads to
Schrödinger’s equation, as pointed out already in section 5. This means that quantum mechanics may be
selected from an infinite set of possible theories by means of a logical principle of simplicity, the statistical
principle of maximal disorder. Considered from this point of view quantum mechanics is ’more reasonable’ than
its classical limit (which is a statistical theory like quantum mechanics). It also means (see section 6) that the
choice
leads to
Schrödinger’s equation, as pointed out already in section 5. This means that quantum mechanics may be
selected from an infinite set of possible theories by means of a logical principle of simplicity, the statistical
principle of maximal disorder. Considered from this point of view quantum mechanics is ’more reasonable’ than
its classical limit (which is a statistical theory like quantum mechanics). It also means (see section 6) that the
choice 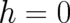 is justified as far as the calculation of expectation values of
is justified as far as the calculation of expectation values of 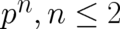 is
concerned.
is
concerned.
In closing this section we note that the particular form of the function 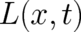 has never been used.
Thus, while the calculation of
has never been used.
Thus, while the calculation of 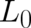 reported in this section completes our derivation of quantum mechanics,
the result obtained is by no means specific for quantum mechanics. Consider the steps leading from the
differential equation (53) and the variational principle (58) to the general solution (61), (67), (68). If we now
supplement our previous assumptions with the composition law (41), we are able to single out the Fisher
reported in this section completes our derivation of quantum mechanics,
the result obtained is by no means specific for quantum mechanics. Consider the steps leading from the
differential equation (53) and the variational principle (58) to the general solution (61), (67), (68). If we now
supplement our previous assumptions with the composition law (41), we are able to single out the Fisher 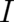 among all solutions [compare e.g. (71) and (70)]. Thus, the above calculations may also be considered as a new
derivation of the Fisher functional, based on assumptions different from those used previously in the
literature.
among all solutions [compare e.g. (71) and (70)]. Thus, the above calculations may also be considered as a new
derivation of the Fisher functional, based on assumptions different from those used previously in the
literature.